8. Задачи на вычисление погрешностей

1. Определить, какое равенство точнее:

9/11 = 0.818 4.24

Находят значения данных выражений с большим числом десятичных знаков:

a₁ = 9/11 = 0.81818… a₂ = 4.2426…

Вычисляют предельные абсолютные погрешности, округляя их с избытком:

Предельные абсолютные погрешности составляют:

%

%

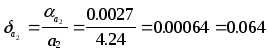Так как , то 9/11=0.818 является более точным.

2. Определить сомнительные цифры числа, оставив верные знаки: а) в узком смысле; б) в широком смысле. Определить абсолютную погрешность результата:

а) 72.353 (0.026) б) 2.3544 =0.2%.

а) Пусть 72.353 (  0.026) = а. Согласно условию, погрешность _а = 0.026 < 0.05 . Это означает, что в числе 72.353 верными в узком смысле являются цифры 7, 2, 3. По правилам округления находят приближенное значение числа, сохранив десятые доли:

а₁ = 72.4;

Полученная погрешность больше 0.05; значит, нужно уменьшить число цифр в приближенном числе до двух:

а₂ = 72;

Так как < 0.5, то обе оставшиеся цифры верны в узком смысле.

б) Пусть а = 2.3544; _а = 0.2%; тогда _а = а * _а = 0.00471. В данном числе верными в широком смысле являются три цифры, поэтому округляем его, сохраняя эти три цифры:

а₁ = 2.35;

Значит, и в округленном числе 2.35 все три цифры верны в широком смысле.

3. Найти предельные абсолютные и относительные погрешности чисел, если они имеют только верные цифры: а) в узком смысле; б) в широком смысле.

а) 0.4357 б) 12.384

а) Так как все четыре числа а = 0.4357 верны в узком смысле, то абсолютная погрешность _а = 0.00005, а относительная погрешность _а = 1 / (2 * 4 * 10³) = 0.000125 = 0.0125% .

б) Так как все пять цифр числа а = 12.384 верны в широком смысле, то _а = 0.001, а относительная погрешность _а = 1 / (1 * 10⁴) = 0.0001 = 0.01% .

4. Вычислить и определить погрешности результата:

где m = 28.3 ( 0.02), n = 7.45 ( 0.01), k = 0.678 ( 0.003)

Вычисляют

m² = 800.9; _m = 0.02 / 28.3 = 0.00071

n³ = 413.5; _n = 0.01 / 7.45 = 0.00135

_k = 0.003 / 0.678 = 0.00443

Тогда

_X = 2 _m + 3 _n + 0.5 _k = 0.00142 + 0.00405 + 0.00222 = 0.00769 = 0.77%

_X = 4.02 10⁵ * 0.0077 = 3.1 10³

Ответ: X = 4.02 10⁵ ( 3.1 10³) ; _X = 0.77%

5. Вычислить и определить погрешности результата:

где n = 3.0567 ( 0.0001) , m = 5.72 ( 0.02)

Имеем n - 1 = 2.0567 ( 0.0001) ; m + n = 5.72 ( 0.02) + 3.0567 ( 0.0001) = 8.7767 ( 0.0201) ; m - n = 5.72 ( 0.02) - 3.0567 ( 0.0001) = 2.6633 ( 0.0201) .

%

Ответ: N  2.54 ( 0.044): _N = 1.74% .

6. Вычислить, пользуясь правилами подсчета цифр

, где h = 11.8 и R = 23.67

V = 3.142 * 11.8² * (23.67 - 3.933) = 3.142 * 11.8² * 19.737 = 3.142 * 139.2 * 19.737 = 437.37 * 19.737 = 8630  8.63 10³ .