6. Основные источники погрешностей

Погрешности могут возникать на отдельных этапах решения задачи:

- Погрешность математической модели - в ней могут быть не учтены какие-либо важные черты рассматриваемой задачи.

- Погрешность исходных данных - это так называемые неустранимые погрешности. Поэтому следует стремиться к тому, чтобы все исходные данные были примерно одинаковой точности.

- Погрешность численного метода - это связано, например, с заменой интеграла суммой, усечением рядов при вычислении значений функции и т.д. Как правило, погрешность численного метода регулируема, т.е. она может быть уменьшена до любого разумного предела (например, изменением шага интегрирования и т.д.). Погрешность метода обычно стремятся довести до величины, в несколько раз меньшей погрешности исходных данных.

- Погрешности вычислений - при использовании ЭВМ неизбежны погрешности, связанные с ограниченностью разрядной сетки ЭВМ (обычно при этом просто отбрасываются лишние цифры). Еще одним источником погрешностей может быть перевод из одной системы счисления в другую. Это может привести к тому, что в новой системе счисления число становится иррациональным.

Уменьшение погрешностей:

1) Пусть требуется найти сумму пяти четырехразрядных чисел:

S = 0.2764 + 0.3944 + 1.475 + 26.46 + 1364 .

Складывая эти числа, а затем округляя полученный результат, получим S = 1393 .

При вычислении на ЭВМ округление происходит после каждого сложения, поэтому предполагая условно сетку машины четырехразрядной сложим эти числа в порядке их записи:

0.2764 + 0.3944 = 0.6708

0.6708 + 1.475 = 2.156

2.156 + 26.46 = 28.62

28.62 + 1364 = 1393 ,

т.е. получили правильный результат .

Если изменить порядок сложения, то получим следующий результат:

1364 + 26.46 = 1390

1390 + 1.475 = 1391

1391 + 0.3944 = 1391

1391 + 0.2764 = 1391

т.е. результат получился менее точным.

Поэтому сложение чисел необходимо проводить по мере их возрастания, т.е. в машинной арифметике из-за погрешности округления существенен порядок выполнения операций.

2) Подобные сложности могут возникать и в других ситуациях, например, при вычислении на ЭВМ значения (а + х)² величина х может оказаться такой, что результатом сложения а + х получится а (при х << a). В этом случае может помочь замена (а+х)² = а² + 2  а  х + х² .

7. Устойчивость. Корректность. Сходимость

1. Устойчивость. Некоторые задачи весьма чувствительны к неточностям в представлении исходных данных. Эта чувствительность характеризуется так называемой устойчивостью.

Задача называется устойчивой по исходному параметру х, если решение y непрерывно от него зависит, т.е. малое приращение исходной величины x приводит к малому приращению искомой величины y .

Отсутствие устойчивости означает, что даже незначительные погрешности в исходных данных приводят к большим погрешностям в решении или даже вовсе к неверному результату. О таких задачах говорят, что они чувствительны к погрешностям исходных данных.

Примером такой задачи является отыскание действительных корней многочленов вида

(x - a)ⁿ = , 0 <  << 1 .

Изменение правой части на величину порядка  приводит к погрешности корней порядка ^1/n .

2. Корректность. Задача называется поставленной корректно, если для любых значений исходных данных из некоторого класса ее решение существует, единственно и устойчиво по исходным данным.

Применять для решения некорректно поставленных задач численные методы, как правило, нецелесообразно, т.к. возникающие при этом погрешности округлений будут сильно возрастать в ходе вычислений, что приведет к значительному искажению результатов.

Для решения некоторых некорректных задач применяют так называемые методы регуляризации. Они основываются на замене исходной задачи корректно поставленной задачей. Последняя содержит некоторый параметр, при стремлении которого к нулю решение этой задачи переходит в решение исходной задачи.

3. Неустойчивость методов. Иногда при решении корректно поставленной задачи может оказаться неустойчивым метод ее решения, Например, для вычисления sin(x) можно использовать следующий степенной ряд:

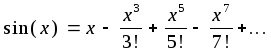
Если вычислить sin(x) при х = 0.5236 (30)при четырех верных знаках и не учитывать члены ряда, меньшие 10^-4, то можно получить

sin(0.5236) = 0.5236 - 0.02393 + 0.0003281 = 0.500 ,

т.е. получен правильный результат.

Если вычислить синус при х = 1470 = 4360+30, то можно получить sin(1470) = 0.5081 . Погрешность при этом составляет около 1%, что объясняется погрешностями округления и способом суммирования (слева направо, без учета величины членов).

Однако для данного ряда при х = 2190 (2190=6360+30) даже при учете членов ряда до 10^-8 и вычислениях с восемью значащими цифрами в результате аналогичных вычислений (суммирование слева направо) получается результат, не имеющий смысла sin(x)=-486.177 .

4. Сходимость. Сходимость означает близость получаемого численного решения задачи к истинному решению. Различают сходимость итерационного процесса и сходимость метода.

Сходимость итерационного процесса - этот процесс заключается в том, что для решения некоторой задачи и нахождения искомого значения определяемого параметра строится метод последовательных приближений. В результате многократного повторения этого процесса (или итераций) получают последовательность значений x₁, x₂, …, x_n, … Говорят, что эта последовательность сходится к точному решению x = a, если при неограниченном возрастании числа итераций предел этой последовательности существует и равен а . В этом случае имеют сходящийся вычислительный процесс.

Другой подход к понятию сходимости используется если задача с непрерывными параметрами заменяется задачей, в которой значения функции вычисляются в фиксированных точках (задачи дискретизации). Это относится, в частности, к численному интегрированию, решению дифференциальных уравнений и т.д. Здесь под сходимостью метода понимается стремление значений решения дискретной модели задачи к соответствующим значениям решения исходной задачи при стремлении к нулю параметра дискретизации (например, шага интегрирования).