4. Общая формула для погрешности

Основная задача теории погрешности заключается в следующем: известны погрешности некоторой системы величин, требуется определить погрешность данной функции от этих величин.

Пусть задана дифференцируемая функция u=(x₁,x₂, ... , x_n) и пусть x_i - абсолютные погрешности аргументов функции.

Тогда предельная абсолютная погрешность функции может быть вычислена по формуле:

Пример. Найти предельную абсолютную и относительную погрешности объема шара V =   d³ / 6 , если диаметр d = 3.7  0.05 см, а  = 3.14 .

Решение. Вычислим частные производные

;

Тогда предельная абсолютная погрешность:

8.44*0.0016 + 21.5*0.05 = 0.013 + 1.075 = 1.088  1.1 см³ .

Поэтому

V =   d³ / 6 = 27.4  1.1 см³

_v = 1.088 / 27.4 см³ = 0.0397 см³  4 %

Предельная относительная погрешность функции вычисляется следующим образом:

Пример. Для определения модуля Юнга по прогибу стержня прямоугольного сечения применяется формула

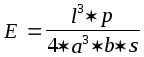
где l - длина стержня, a и b - измерения поперечного сечения стержня, s - стрела прогиба, p - нагрузка.

Вычислить предельную абсолютную погрешность при определении модуля Юнга, если p = 20 кг; _p = 0.1% ; a = 3 мм; _а = 1%; b = 44 мм; _b = 1%; l = 50 мм; _l = 1%; s = 2.5 см; _s = 1% .

Решение.

Ln(E) = 3  Ln(l) + Ln(p) - 3  Ln(a) - Ln(b) - Ln(s) - Ln(4) .

Отсюда, заменяя приращения дифференциалами, будем иметь

Следовательно:

_Е = 3  _l + _p + 3  _a + _b + _s = 3  0.01 + 0.001 + 3  0.01 + 0.01 + 0.01 = 0.081

Таким образом, предельная относительная погрешность составляет примерно 8% от измеряемой величины, т.е.

E = (2.10  0.17)  10 ⁶ кг.см² .

5. Обратная задача теории погрешностей

На практике также важна обратная задача: каковы должны быть абсолютные погрешности аргументов функции, чтобы абсолютная погрешность функции не превышала заданной величины.

Эта задача математически не определена, так как заданную предельную погрешность u функции f(x₁,x₂,…,x_n) можно обеспечить, устанавливая по-разному предельные абсолютные погрешности x_i ее аргументов.

Простейшее решение обратной задачи дается так называемым принципом равных влияний. Согласно этому принципу предполагается, что все частные дифференциалы f/x_i  x_i одинаково влияют на образование общей абсолютной погрешности u функции f(x₁,x₂,…,x_n).

Тогда искомая формула легко получается из формулы предыдущего раздела:



Пример. Радиус основания цилиндра R = 2 м, высота цилиндра H = 3 м. С какими абсолютными погрешностями надо определить R и H, чтобы его объем V можно было вычислить с точностью до 0.1 м³ ?

Решение. Имеем и V = 0.1 м³.

Полагая R=2 м, H=3 м и =3.14 приближенно получаем

V/ = R²  H = 12

V/R = 2    R  H = 37.7

V/H =   R² = 12.6

Так как число параметров n = 3, то будем иметь

 = 0.1 / (3  12) < 0.003

R = 0.1 / (3  37.7) < 0.001

H = 0.1 / (3  12.6) < 0.003

Нередко при решении обратной задачи можно столкнуться с таким случаем, когда найденные по приведенной формуле предельные абсолютные погрешности отдельных независимых переменных окажутся настолько малыми, что добиться соответствующей точности при измерении этих величин практически невозможно. В таких случаях разумно уменьшают погрешности одной части переменных, чтобы добиться увеличения погрешностей другой части переменных.

Пример. С какой точностью надо измерить радиус круга R = 30.5 см и со сколькими знаками взять , чтобы площадь круга была известна с точностью до 0.1% ?

Решение. Имеем s =   R² . Используя общие правила работы с приближенными числами можно записать:

По принципу равных частей следует положить:

и

Отсюда  = 3.14*0.0005=0.00157  0.0016 и R  0.00025  R = 0.0076 см .

Таким образом если взять  = 3.14, то необходимо измерять R с точностью до тысячных долей сантиметра, что практически трудно осуществить.

Поэтому выгоднее поступить следующим образом: взять  = 3.142. В этом случае (по формуле в разделе о значащих цифрах) _ = 0.00016 . Тогда 2  R/R = 0.001 - 0.00016 = 0.00084 и R= 0.00084*30.5 / 2 = 0.01281 см, что уже можно выполнить практически.