10.3 Оценка погрешности для метода трапеций

При использовании метода трапеций возникает ошибка, равная сумме площадей между кривой y=f(x) и хордами, соединяющими точки y_i и y_i+1.

Для оценки этой погрешности можно разложить функцию y=f(x) в ряд Тейлора в точках x_i и x_i+1. Это разложение позволит получить уравнение исходной кривой в виде, удобном для сравнения точного значения интеграла с приближенным, вычисленным по методу трапеций.

Разложим функцию y=f(x) в ряд Тейлора в окрестности точки x=x_i:

Аналогично, разлагая функцию в ряд в окрестности точки x_i+1 = x_i + h :

Обе эти формулы справедливы, но ни одна из них в отдельности не позволяет получить нужный результат. Поэтому берут среднее значение из обеих формул:

Интегрируя y dx от x_i до x_i+1 , получают:

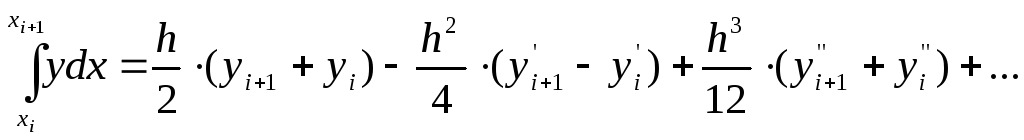
Это выражение представляет собой оценку истинного значения интеграла. Оценка может быть сделана как угодно точной, потому что можно взять сколь угодно большое количество членов в разложении функции в ряд Тейлора.

Правило трапеций получается, если в этой формуле отбросить все члены, содержащие h в степенях выше первой. Поэтому можно записать:

где

Для малых h первый член гораздо больше всех остальных, поэтому можно предположить, что ошибка как раз им и определяется. Поэтому можно записать:

где константу К необходимо определить. Конечно, это будет только некоторое приближение, основанное на допущении о постоянстве К; такое приближение справедливо только до тех пор, пока y^’’ и производные высших порядков не изменяются сильно между x_i и x_i+1.

При определении К необходимо помнить, что формула справедлива для любой функции. Поэтому можно взять любую функцию, для которой погрешность при интегрировании по методу трапеций не будет равна нулю. Результат будет справедлив для всех функций. Если взять функцию y = x, то можно легко убедиться, что погрешность равна нулю, т.е. метод трапеций дает точный результат при интегрировании линейных функций.

Возьмем y = x². В этом случае:

Но, с другой стороны, если в формулу подставить y_i = x_i² и y_i+1 = (x_i + h)², то можно получить:

Приравнивая два последних уравнения, легко получить:

Но так как y’ = 2x, то можно получить

Поэтому для К получают

И окончательно

Полную погрешность можно оценить из соотношения

где y_b^’ равно значению df/dx при x = b и y_a^’ равно значению df/dx при x = a.

Чаще погрешность для метода трапеций выражают с помощью несколько преобразованной формулы. На основании теоремы о среднем в интегральном исчислении

, где a £ x £ b

можно, положив , записать f(x) = y’(x). Отсюда

y_b - y_a = (b-a)×y’(x)

После еще одного дифференцирования можно получить

где a £ x £ b, так что

Более того, если в интервале a £ x £ b имеется M = max { y^’’(x) }, то

10.4 Метод парабол

В этом методе вершины каждых трех ординат соединяются дугами квадратичных парабол, оси которых параллельны оси y. Таким образом, вместо двух прямоугольных трапеций рассматривают одну элементарную трапецию, ограниченную параболической дугой. Исходя из этого можно видеть, что число разбиений n в методе Симпсона должно быть четным.

Площади полученных трапеций можно обозначить как s₁₂, s₃₄, … , s_n-1,n. Рассмотрим первую из этих трапеций. Для упрощения вычислений можно перенести ось ординат параллельно самой себе так, чтобы она шла вдоль ординаты y_o . Ясно, что от этого величина площади не изменится.

Уравнение квадратичной параболы , ось которой па­раллельна оси y, есть

y = A₀ + A₁*x + A₂*x²

Чтобы парабола проходила через точки подынтег­ральной кривой (x_o,y_o), (x₁,y₁), (x₂,y₂) нужно правильно подобрать коэффициенты А₀, А₁ и А₂:

Так как x_o = 0, x₁ = h и x₂ = 2h, то, подставив эти значения в приведенное выше уравнение можно получить:

После решения этой системы можно найти:

; ;

Площадь s₁₂ определяется интегралом:

Подставив найденные значения А₀, А₁ и А₂ в это уравнения и приведя свободные члены, получим:

Аналогично

. . . . . . . . . .

Следовательно,

Отсюда можно найти формулу метода парабол (или метода Симпсона):

Или, в более компактном виде:

где c_j = 1, 4, 2, 4, 2, … ,2, 4, 1 .

Предельная абсолютная погрешность метода Симпсона:

, где

Пример 1: вычислить приближенно по формуле Симпсона с точностью до 0.001.

Решение: нужно вычислить какой шаг h нужно взять для достижения заданной точности. Для этого вычисляют

; ;

;

Наибольшее значение ½f ^IV(x)½ на отрезке [ 0;1 ] достигается в точке х=0: ½f ^IV(x)½ = 3. Значит:

Так как эта погрешность должна быть меньше 0.001, то h⁴/60 £ 0.001, т.е. h⁴ £ 0.06. Можно принять h = 0.5 (если h = 0.5, то h⁴ = 0.0625), т.е. несколько больше нужной величины. Итак, для достижения требуемой точности достаточно разбить интервал пополам.

Вычисления нужно провести с одним запасным знаком:

Округляя последний член можно получить I » 1.148 .

Можно вычислить точное значение этого интеграла по формуле Ньютона-Лейбница:

Таким образом, значение этого интеграла, вычисленное по методу Симпсона, имеет четыре верных знака после запятой.

Если вычисление четвертой производной подынтегральной функции затруднительно, то для оценки погрешности вычисления интеграла по методу Симпсона можно использовать следующую стратегию.

• Пусть интеграл вычислен по формуле Симпсона дважды при различных значениях h. Пусть I₁, h₁, d₁ - соответственно обозначают найденный результат, значение шага и погрешность первого вычисления, а I₂, h₂, d₂ - то же при втором вычислении.

• Согласно формуле оценки погрешности, имеем

, или

• Отсюда, в частности если h₂ = h₁/2, то получают, что d₁ = 16*d₂ и для точного значения интеграла S при двух вычислениях с шагом h₁ и h₂ = h₁/2, имеют

S = I₁ + d₁ = I₁ + 16*d₂

S = I₂ + d₂

• Отсюда, отняв верхнее уравнение от нижнего, находят , или, применяя более общие выражения, .

Следовательно, если по формуле Симпсона вычислить интеграл разделив отрезок [ a,b ] первый раз на n частей, а второй - на 2n частей, то для второго результата I_2n погрешность приблизительно будет равняться 1/15 разности результатов I_2n и I_n .

Этот способ называют оценкой погрешности формулы Симпсона по методу удвоения шага вычислений.

Пример 2: вычислить по формуле Симпсона , приняв n = 8. Вычисления вести с шестью знаками после запятой. Оценить погрешность полученного результата, пользуясь способом удвоения шага вычислений; сравнить результат с истинным значением интеграла, взяв последнее с одним запасным (седьмым) знаком.

Решение: находим значение подынтегральной функции:

I	0	1	2	3	4	5	6	7	8
x	0	0.125	0.250	0.375	0.500	0.625	0.750	0.875	1
f(x)	1.000000	0.984625	0.941176	0.876712	0.800000	0.719101	0.640000	0.566389	0.500000

Нужно подставить эти значения в формулу Симпсона при h₁ = 0.250 и h₂ = 0.125:

Отсюда

Таким образом, все шесть знаков I_2n должны быть точными.

Истинное значение интеграла равно:

что подтверждает полученный результат.

Рассмотренные методы прямоугольников, трапеций и парабол, являются частным случаем (при m=0, m=1 и m=2) общей квадратурной формулы Ньютона-Котеса, которую получают, заменив подынтегральную функцию полиномом m-ой степени. Кроме формулы Ньютона-Котеса есть ряд других квадратурных функций. Наиболее точной из них является формула Гаусса, которая при n точках промежутка интегрирования обеспечивает совершенно точные результаты для полинома (2n+1)-й степени. Точки деления в формуле Гаусса берут не на равных расстояниях одна от другой, а выбирают по определенному правилу.