- 7-

Математическая обработка данных

Математическая обработка данных Постановка задачи

Очень часто некоторое явление характеризуется двумя варьируемыми величинами x и y, из которых x выбирается как независимая, а y - как зависимая переменная величина. Обычно предполагают, что между переменными x и y существует однозначное соответствие, т.е. каждому значению независимой величины x соответствует с заданной степенью точности одно значение зависимой переменной y .Такая зависимость может быть изображена в виде функции y = f(x), причем аналитическое выражение этой функции пока не известно.

В общем виде задачу можно сформулировать следующим образом: пусть в результате исследования некоторой величины x значениям x₁, x₂, … , x_n поставлены в соответствие значения y₁, y₂, … , y_n некоторой величины y. Требуется подобрать вид аналитической зависимости y = f(x), связывающие переменные x и y.

Аналитические зависимости, полученные в результате наблюдений, обычно называют эмпирическими. Выявление эмпирических зависимостей делятся на два основных этапа - 1) выбор эмпирической формулы и 2) уточнение коэффициентов выбранной формулы.

Для второго этапа наиболее распространены три метода определения коэффициентов формульных зависимостей:

• метод выбранных точек;

• метод средних;

• метод наименьших квадратов (МНК).

Построение эмпирических линейных зависимостей

Построение зависимости y = bx

Пусть имеются следующие экспериментальные данные, описывающие количество выпускаемых изделий (y) в зависимости от времени работы (x):

x	0	1	1.5	2.5	3	4.5	5	6
y	0	67	101	168	202	301	334	404

Требуется выявить вид эмпирической зависимости и вычислить ее параметры.

После построения графика хорошо видно, что в данном случае имеют прямую, проходящую через начало координат.

Т.е. в данном случае мы имеем уравне­ние

y = bx .

Для уточнения параметра а можно воспользоваться перечисленными выше тремя способами.

• Метод выбранных точек - для этого проводят прямую как можно ближе к нанесенным точкам. На этой прямой выбирают произвольную точку M(x*,y*), координаты которой определяют из графика. Пусть x*=5.6, отсюда y*=375. Тогда b=375/5.6=66.96. Т.е. уравнение прямой, проходящей через начало координат примет вид

  y = 66.96x .

  Недостаток метода - величина коэффициента b существенно зависит от того, как была проведена исходная прямая.

• Метод средних - параметр b определяется из условия минимума средней ошибки:

  или .

  В этой формуле накапливается разность между истинным или экспериментальным -y_i и расчетным (y_i*) значением величины y.

  Последнее выражение можно переписать в виде

  , откуда .

  Таким образом

  

  Следовательно, искомая зависимость имеет вид y = 67.11x

• Метод наименьших квадратов - в этом методе параметр b определяется из условия минимума суммы квадратов отклонений экспериментальных значений y_i от расчетных величин y_i*.

  или .

  Минимальное значение суммы квадратов отклонений (критерия рассогласования) можно найти из условия равенства нулю производной по параметру а от функции . После дифференцирования можно получить

  или .

  Отсюда

  

  Чтобы воспользоваться этой формулой обычно составляют вспомогательную таблицу:

xi	yi	xiyi	xi2
1	67	67.0	1
1.5	101	151.5	2.25
2.5	168	420.0	6.25
3	202	606.0	9
4.5	301	1354.5	20.25
5	334	1670.0	25
6	404	2424.0	36
		Sxiyi=6693.0	Sxi2=99.75

Теперь можно найти b = 6693.0/99.75=67.09

Т.е. в результате найдено уравнение y=67.09x .

Итак в результате было получено три уравнения, из которых наиболее точным является уравнение, полученное по МНК, но этот метод требует большего объема вычислений.

Построение линейной зависимости y = a + bx

Пусть имеются следующие данные, описывающие рост численности населения (y) в некотором городе в зависимости от года (х):

x	1946	1948	1950	1952	1954	1956	1958	1960
y	50 000	68 500	92 500	110 000	132 500	152 000	175 000	195 000

Аналитическая зависимость в этом случае (как видно из графика), описывается уравнением

y = a + bx .

Для уточнения параметров a и b используют те же три метода:

• Метод выбранных точек - чтобы вычислить параметры a и b, необходимо составить систему двух линейно независимых уравнений. Для этого выбирают на графике две произвольные точки M₁ (x₁*,y₁*) и M₂ (x₂*,y₂*) и подставив численные значения координат этих точек в исходное уравнение, получим систему

  

  Решая ее получают искомые значения.

  Например, на графике выбираем точки M₁ и M₂ с координатами x₁*=1949, y₁*=80000 и x₂*= 1959, y₂*=184000 .В результате имеем систему:

  

  Решая ее получаем а = -20 189 600 , b = 10400, т.е. искомая зависимость принимает вид

  y = -20 189 600 + 10400 x .

• Метод средних - согласно этому методу, лучшим положением прямой является такое, для которого алгебраическая сумма всех отклонений вычисленных значений от опытных равна нулю.

  Для определения параметров a и b эмпирической прямой табличные данные делят на две группы и для каждой из них записывают:

  и

  где k и n-k - количество табличных данных соответственно для первой и второй группы.

  Заменив сумму разностей разностью сумм и, сделав преобразования, получают:

  

  Решая эту систему находят искомые коэффициенты.

  Для их нахождения в искомом примере разбивают все данные на две группы таким образом, чтобы суммы y_i в них были примерно одинаковы.

xi	Sxi	yi	Syi
1946		50 000
1948		68 500
1950	9750	92 500	453 500
1952		110 000
1954		132 500
1956		152 000
1958	5874	175 000	522 000
1960		195 000

В результате получается следующая система

решая которую находят a = - 20 213 675 и b = 10412.5 .

Искомая модель

y = -20 213 675 + 10 412.5 x .

• Метод наименьших квадратов - согласно МНК

Используя необходимое условие существования экстремума функции нескольких переменных, получим:

Или

Отсюда

Для вычисления параметров линейной зависимости для исходного примера необходимо составить вспомогательную таблицу

xi	yi	xiyi	xi2
1946	50 000	97 300 000	3 786 916
1948	68 500	133 438 000	3 794 704
1950	92 500	180 375 000	3 802 500
1952	110 000	214 720 000	3 810 304
1954	132 500	258 905 000	3 818 116
1956	152 000	297 312 000	3 825 936
1958	175 000	342 650 000	3 833 764
1960	195 000	382 200 000	3 841 600
Sx=15 624	Sy=975 500	Sxiyi=1 906 900 000	Sxi2=30 513 840

Для нахождения коэффициентов последняя система может быть переписана в следующем виде:

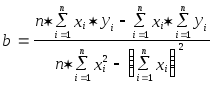и

После решения: a = -20 114 095 и b = 10 361.481. Искомая модель

y = -20 114 095 + 10 361.481 x