Вывод условия сходимости:

Так как x = j(x) и x_n = j(x_n-1), то можно записать

По теореме о среднем (она утверждает, что если производная функции f(x) непрерывна на некотором интервале [a,b], то тангенс угла наклона хорды, проведенной между точками a и b (т.е. {f(b)-f(a)/(b-a)} равен производной функции в некоторой промежуточной точке, лежащей между a и b) частное в последнем выражении будет равно j'(C), где С - некоторая промежуточная точка в интервале поиска корня.

Следовательно

x_n - x = j ' (C) × (x_n-1 - x)

Если ввести обозначение M = max½j ' (x)½ для всего интервала поиска, то предыдущее равенство может быть переписано в виде:

½x_n - x½ £ M × ½x_n-1 - x½

Аналогично

½x_n-1 - x½ £ M × ½x_n-2 - x½

Тогда для ½x_n - x½ будет справедливо неравенство:

½x_n - x½ £ M ² × ½x_n-2 - x½

и т.д.

Продолжая эти выкладки дальше, в результате получаем

½x_n - x½ £ M ⁿ × ½x₀ - x½

где n - натуральное число.

Чтобы метод сходился, необходимо выполнение неравенства:

½x_n - x½ < M ⁿ × ½x₀ - x½

Отсюда следует, что M = max½j ' (x)½ должно быть меньше единицы.

В свою очередь, для всех остальных значений j ' (x) меньших М, можно записать:

½j ' (x)½ < 1

Блок-схема метода

Ввод с,e

x=f(c)

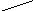
½x-c½<e (Нет) c=x

(Да)

Вывод x

Пример. Решить линейное уравнение

2x - 1 = 0 .

Для этого уравнения возможны, например, следующие итерационные формы:

2.5x - 0.5x -1 =0

x = 5x - 2 ½j'(x)½ = 5 > 1 .

x = 0.2x + 0.4 ½j'(x)½ = 0.2 < 1

1.3x +0.7x - 1 = 0

x = -1.857x+1.428 ½j'(x)½ = 1.857 > 1

x = -0.538x + 0.769 ½j'(x)½ = 0.538 < 1

10x - 8x - 1 =0

x = 1.125x - 0.125 ½j'(x)½ = 1.125 > 1

x = 0.8x + 0.1 ½j'(x)½ = 0.8 < 1

Если выбрать подходящие итерационные формы и провести решение этого уравнения (с точностью 0.01), то получатся различные результаты

j(x)		0.2x + 0.4			-0.54x + 0.769			0.8x + 0.1
n	x		j(x)	x		j(x)	x		j(x)
0	1.000		0.600	1.000		0.231	1.000		0.900
1	0.600		0.520	0.231		0.645	0.900		0.820
2	0.520		0.504	0.645		0.422	0.820		0.756
3	0.504		0.501	0.422		0.542	0.756		0.705
4				0.542		0.477	0.705		0.664
5				0.477		0.512	0.664		0.631
6				0.512		0.494	0.631		0.605
7				0.494		0.503	0.605		0.584
8				0.503		0.498	0.584		0.567
9							0.567		0.554
10							0.554		0.543
11							0.543		0.534
12							0.534		0.527
13							0.527		0.522

Как видно, в третьем случае точное решение не попадает в найденный интервал. Кроме этого, следует обратить внимание на характер сходимости - в первом и третьем случаях она - монотонная, а во втором случае - колебательная.

Чтобы исключить такую ситуацию применяют следующий подход:

Пусть x - точное значение корня уравнения х = j(x), а число q определяется из соотношения ½j'(x)½ £ q < 1. Тогда справедливо соотношение (вывод см. ниже):

.

Если поставить условие, что истинное значение корня x должно отличаться от приближенного значения на величину e, т.е. ½x - x_n½£e, то приближения x₀, x₁, … , x_n надо вычислять до тех пор, пока не будет выполнено неравенство

или

и тогда x = x_n ± e

Для нашего примера q=0.8 и тогда

Вывод формулы:

Рассмотрим два последовательных приближения: х_n = j(x_n-1) и х_n+1 = j(x_n).Отсюда x_n+1 - x_n = j(x_n) - j(x_n-1) . Используя теорему о среднем (она утверждает, что если производная функции f(x) непрерывна на некотором интервале [a,b], то тангенс угла наклона хорды, проведенной между точками a и b (т.е. {f(b)-f(a)}/(b-a) ) равен производной функции в некоторой промежуточной точке, лежащей между a и b) можно получить:

На основании условия ½j'(x)½ £ q < 1 можно записать:

½ x_n+1 - x_n ½£ q * ½x_n - x_n-1 ½ .

С другой стороны, пусть f(x) = x - j(x). Очевидно, что f '(x) = 1 -j'(x) ³ 1 - q. Отсюда, учитывая, что f(x)=0, получим

½ x_n - j(x_n)½ = ½f(x_n) - f(x)½ = ½x_n - x½*½f ' (x_n)½ ³ (1 - q)* ½x_n - x½,где x_nÎ(x_n,x)

Тогда

или

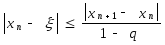
Используя предыдущую формулу можно получить:

Приведение уравнения f(x)=0 к виду x=j(x) для обеспечения выполнения неравенства ½j '(x)½ < 1

В общем случае получить подходящую итерационную форму возможно, проведя равносильное преобразование исходного уравнения, например, умножив его на коэффициент l:`

l*f(x) = 0 .

Прибавив затем к обеим частям уравнения х и обозначив

j(x) = x + l*f(x)

можно потребовать выполнения достаточного условия

½1+l*f '(x)½ < 1

Отсюда определяется необходимое значение l

- 2 < l * f '(x) < 0, sign(l) = - sign(f '(x)) .

Так как условие ½j'(x)½ < 1 должно выполняться на всем отрезке [a,b], то для выбора l следует использовать наибольшее значение f '(x) на этом отрезке, т.е.

, sign((l) = - sign{f '(x)} .

Это соотношение определяет диапазон значений коэффициента l, изменяющий величину

j'(x) = 1 +l * f '(x)

в пределах ( -1 ; +1 ).

Обычно принимают

, sign(l) = - sign(max{f '(x)}) .

В случае линейной функции этот подход приводит к следующему:

f(x) = a + bx

j(x) = x + l(a + bx) .

Наилучшее значение l = - 1/f ' (x) = - 1/b . В этом случае сразу получается точное значение корня:

В общем случае коэффициент l должен изменять значения функции f(x) в разных точках отрезка [a,b] на различную величину в зависимости от ее кривизны, т.е. также быть функцией l(х). Поэтому на каждой итерации возможна коррекция первоначально рассчитанной величины l, т.е. вычисления в каждой точке x^k значения l^k :

, sign(l^k) = - sign(f '(x^k)) .

Так как метод итерации сходится при любом выборе начального значения x₀ из отрезка [a,b], то он является самоисправляющимся, т.е. отдельная ошибка в вычислениях, не выходящая за пределы отрезка [a,b], не влияет на конечный результат.

Пример. Решить методом простой итерации уравнение f(x) = x² - 0.6 на отрезке [0; 1] с точностью 0.025 .

Для решения исходное уравнение приводится к виду

x = x + l * (x² - 0.6) .

Для выбора величины l используют приведенную выше формулу l=- 1/ max{f '(x)} = - 1/(2x) = - 1/2 .

Тогда расчетная формула имеет вид

x_i+1 = - 0.5x_i² + x_i + 0.3

В качестве начального приближения можно выбрать верхнюю границу заданного отрезка х₀ = 1 .

n	xi	xi+1	½xi+1 - xi½
0	1	0.8	0.2
1	0.8	0.78	0.02