Блок-схема метода

Ввод a,b,e,x

h=-f(x)/f '(x)

x = x + h

Да a £ x £ b Нет

Сокращение отрезка, выбор x

Нет ½h½£e

Да

Вывод x,f(x)

Пример. Вычислить методом Ньютона отрицательный корень уравнения f(x) = x⁴ - 3x² + 75x - 10000 = 0.

Проведя отделение корня можно убедиться, что корень локализован на интервале [-11, -10] : f(-11) = 3453, f(-10) = -1050 . В этом интервале f '(x) < 0 и f "(x) > 0. Так как f(-11) > 0 и f "(-11) > 0, то за начальное приближение можно принять x₀ = -11.

N	xn	f(xn)	f '(xn)	hn = -f(xn)/f '(xn)
0	-11	3453	-5183	0.6662
1	-10.3336	307.3	4276.8	0.0718
2	-10.2618	3.496	4185.9	0.0008
3	-10.261	0.1477	-	-

Останавливаясь на n = 3, проверяем знак значения f(x_n+0.001) = f(-10.260) . Так как f(-10.260) < 0, то -10.261 < x < -10.260, и любое из этих чисел дает искомое приближение.

Видоизмененный метод Ньютона

Если производная f '(x) мало изменяется на отрезке [a,b], то в расчетной формуле метода можно положить:

f '(x_n) » f '(x₀) .

Отсюда для корня x уравнения f(x) = 0 получаем последовательные приближения

, (n = 0, 1, 2, …)

Геометрически этот способ означает, что касательные заменяются прямыми, параллельными касательной к кривой y = f(x), в ее фиксированной точке x₀ . Этот способ избавляет от необходимости вычислять каждый раз значения производной, поэтому эта формула полезна, если f '(x) сложна.

Если есть время, то дать метод секущих с самостоятельным выводом формулы относительно точек x_i-1, x_i и x_i+1. Показать, что одним из вариантов метода секущих является нижеприведенный метод.

Для сложных функций вычисление производных может представлять значительные трудности. В этом случае вместо производной в итерационную формулу можно подставить ее конечно-разностное значение:

и тогда можно записать

Для использования этой формулы необходимо выбрать две начальные точки - х₀ и х₁. Эта формула объединяет достоинства метода секущих и касательных, так как в этом случае приближение к корню происходит с двух сторон.

Провести графическое сравнение метода касательных, хорд и секущих и показать, что в принципе это один и тот же метод - вся разница только в способе вычисления производной: при аналитическом вычислении получаем метод касательных, если производная считается на всем интервале - метод хорд и, наконец, если используется конечно-разностное соотношение - то метод секущих..

Метод итерации (метод последовательных приближений)

Сущность этого метода заключается в следующем. Пусть дано уравнение f(x) = 0, где f(x) - непрерывная функция, и требуется определить ее вещественные корни. Для этого заменяют исходное уравнение равносильным:

x = j(x).

Выбрав приближенное значение корня x₀ подставляют его в правую часть этого уравнения. Тогда получают:

x₁ = j(x₀).

После этого процесс продолжают:

x₂ = j(x₁) … x_n = j(x_n-1).

Если эта последовательность - сходящаяся, т.е. существует предел , то, переходя к пределу в выраженииx_n = j(x_n-1) и предполагая функцию j(x) непрерывной, можно найти:

или

x = j(x).

Таким образом, предел x является корнем уравнения и может быть вычислен по приведенной формуле с любой степенью точности.

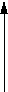
На приведенных рисунках процесс итерации сходится (кривая y = j(x) в окрестности корня x - пологая, т.е. ½j '(x)½ < 1).

Однако, если рассмотреть случай, где ½j'(x)½ > 1, то процесс итерации может быть рас­ходящимся.

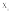
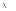
Поэтому для практического применения ме­тода итерации нужно выяснить достаточные условия сходимости итерационного процесса.

Пусть функция j(x) определена и диффе­ренцируема на отрезке [a,b], причем все ее зна­чения j(x) Î [a,b].

Тогда, если выполняется условие

½j '(x)½ < 1

при a < x < b, то:

1) процесс итерации x_n = j(x_n-1) (n=1,2,…) сходится независимо от начального значения x₀ Î [a,b];

2) предельное значение является единственным корнем уравненияx = j(x) на отрезке [a,b] .

Если это условие выполняется не на всем интервале, то метод может как сходиться, так и расходиться.