Способ пропорциональных частей (метод хорд)

Пусть для определенности f(a) < 0 и f(b) > 0. Тогда, вместо того, чтобы делить отрезок [a,b] пополам, более естественно разделить его в соотношении f(a)/f(b) . Это дает приближенное значение корня x₁ = a + h .

Для вычисления значения h можно составить пропорцию (см.рисунок)

Откуда

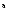
Далее, применяя этот прием к тому из отрезков [a,x] или [b,x], на концах которого функция f(x) имеет противоположные знаки, получим второе приближение корня и т.д.

Геометрически способ пропорциональ­ных частей эквивалентен замене кривой y = f(x) хордой, проходящей через точки A [a, f(a)] и B [b, f(b)]. Отсюда можно получить еще одну формулу этого метода. Из подобия треугольников вытекает, что

. Отсюда

Блок-схема метода

Ввод a,b,e

x = a + x

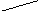
Да f(a)*f(x) < 0 Нет

b = x a = x

Нет ½h½£e

Да

Вывод x,f(x)

Пример. Найти положительный корень уравнения f(x) = x³ - 0.2x² - 0.2x -1.2 = 0 с точностью до 0.002 .

n	a	b	h	x	f(a)	f(b)	f(x)
1	1	1.5	0.1481	1.1481	-0.6	1.425	-0.1799
2	1.1481	1.5	0.0390	1.1871	-0.1799	1.425	-0.0464
3	1.1871	1.5	0.0099	1.1970	-0.0464	1.425	-0.0109
4	1.197	1.5	0.0023	1.1993	-0.0109	1.425	-0.0025
5	1.1993	1.5	0.0005	1.1998	-0.0025	1.425

Так как на пятом шаге величина шага стала меньше заданной точности, то поиск корня можно прекратить. Это равносильно неравенству

½ x_n - x_n-1 ½ < e .

Как видно из этого примера для простых функций в методе хорд один из концов отрезка остается закрепленным. Поэтому можно сказать, что

1) неподвижен тот конец, для которого знак функции f(x) совпадает со знаком ее второй производной f "(x).

2) последовательные приближения x_n лежат по ту сторону корня x, где функция f(x) имеет знак, противоположный знаку ее второй производной f "(x) .

Метод секущих сходится быстро, если функция f(x) имеет малую кривизну (f"(x) - мало).

Метод Ньютона (метод касательных)

Пусть корень x уравнения f(x) = 0 отделен на отрезке [a,b], причем f '(x) и f "(x) непрерывны и сохраняют определенные знаки при a £ x £ b. Найдя какое-нибудь n-е приближение корня x_n » x (a £ x_n £ b), можно уточнить его по методу Ньютона следующим образом. Положим x = x_n + h_n , где h_n считают малой величиной. Отсюда, применяя формулу Тейлора, получим

0 = f(x_n + h_n) » f(x_n) + h_n f '(x_n) .

Следовательно,

Отсюда можно найти следующее (по порядку) приближение корня:

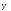
, (n = 0, 1, 2, …)

Как видно из этого рисунка правильный выбор начального приближения обеспечивает удачу в по­иске корня. Общее правило - "хорошим" начальным приближением является то, для которого выполня­ется неравенство:

f(x₀) f "(x₀) > 0 .

Из общей формулы метода вытекает, что чем больше численное значение первой производной в окрестности данного корня, тем меньше поправка, которую нужно прибавить к n-му приближению, чтобы получить n+1 приближение. Поэтому метод Ньютона удобно применять тогда, когда в окрестности данного корня график функции имеет большую крутизну. Но если численное значение первой производной близ корня мало, то поправки будут велики, и вычисление корня по этому методу может оказаться очень долгим, а иногда и вовсе невозможным.