Блок-схема метода Эйлера

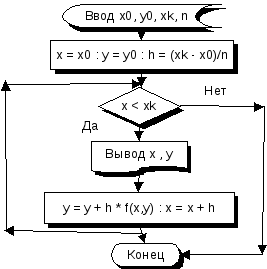
Пример: Решить методом Эйлера дифференциальное уравнение y'=2x² - y на интервале [0 , 5] при начальных условиях y(0) = 1.

Решение: Выбираем число разбиений n = 5. Тогда h = (5 - 0)/5 = 1 .

n	x	y	f(x,y)
0	0.000	1.000	-1.000
1	1.000	0.000	2.000
2	2.000	2.000	6.000
3	3.000	8.000	10.000
4	4.000	18.000	14.000
5	5.000	32.000

Если выбрать число разбиений n = 10, то h = (5 - 0)/10 = 0.5 .

n	x	y	f(x,y)	h * f(x,y)
0	0.000	1.000	-1.000	-0.500
1	0.500	0.500	0.000	0.000
2	1.000	0.500	1.500	0.750
3	1.500	1.250	3.250	1.625
4	2.000	2.875	5.125	2.562
5	2.500	5.437	7.062	3.531
6	3.000	8.968	9.032	4.516
7	3.500	13.484	11.016	5.508
8	4.000	18.992	13.008	6.504
9	4.500	25.496	15.004	7.502
10	5.000	32.998

Модифицированный метод Эйлера

В отличие от обычного метода Эйлера, когда для вычисления следующей точки интегральной кривой (x_i+1, y_i+1) требуется информация только о предыдущей точке (x_i, y_i), модифицированный метод основан на использовании информации о некоторой промежуточной точке (x_n, y_n) . Порядок построения решения в модифицированном методе Эйлера представлен на рисунке и заключается в следующем:

1) Через точку (x_i, y_i) проводится касательная с тангенсом угла наклона tg(a₁) = f(x_i , y_i) до пересечения с прямой x_n = x_i + h/2 . В полученной точке пересечения А₂ по методу Эйлера рассчитывается значение функции y_n = y_i + h/2 * y'_i и вычисляется новая производная

f(x_n, y_n) = f(x_i + h/2 , y_i + h/2 * y'_i)

2) Значение этой производной определяет тангенс угла наклона второй касательной tg(a₂) , которая проводится через точку А₂ .

3) Далее осуществляется возврат в исходную точку А₁ и через нее проводится прямая, параллельная второй касательной до пересечения с прямой x = x_i+1 .

Тогда

y_i+1 = y_i + h * tg(a₂) = y_i + h * f(x_i + h/2 , y_i + h/2 * y'_i)

Таким образом, при использовании модифицированного метода Эйлера на каждом шаге интегрирования необходимо иметь информацию о предыдущей и последующей точках. Поэтому этим методом нельзя пользоваться на первом шаге интегрирования из начальной точки. На первом шаге обычно применяется простой метод Эйлера, после чего на последующих шагах уже можно воспользоваться расчетным соотношением модифицированного метода:

y_i+1 = y_i + h * f(x_i + h/2 , y_i + h/2 * y'_i)

x_i+1 = x_i + h

Точность решения в модифицированном методе Эйлера увеличивается благодаря тому, что расчет функции на каждом шаге интегрирования выполняется два раза.

Пример: решить то же уравнение модифицированным методом Эйлера.

Решение:

1) Выбираем число разбиений n = 5. Тогда h = (5 - 0)/5 = 1 .

n	x	y	x1=x+h/2	y'	y1=y+h/2*y'	f(x1,y1)	h*f(x1,y1)
0	0.000	1.000	0.500	-1.000	0.500	0.000	0.000
1	1.000	1.000	1.500	1.000	1.500	3.000	3.000
2	2.000	4.000	2.500	4.000	6.000	6.500	6.500
3	3.000	10.500	3.500	7.500	14.250	10.250	10.250
4	4.000	20.750	4.500	11.250	26.375	14.125	14.125
5	5.000	34.875

2) Если выбрать число разбиений n = 10, то h = (5 - 0)/10 = 0.5 .

n	x	y	x1=x+h/2	y'	y1=y+h/2*y'	f(x1,y1)	h*f(x1,y1)
0	0.000	1.000	0.250	-1.000	0.750	-0.625	-0.313
1	0.500	0.688	0.750	-0.188	0.641	0.484	0.242
2	1.000	0.930	1.250	1.070	1.197	1.928	0.964
3	1.500	1.894	1.750	2.606	2.545	3.580	1.790
4	2.000	3.683	2.250	4.317	4.763	5.362	2.681
5	2.500	6.365	2.750	6.135	7.899	7.226	3.613
6	3.000	9.978	3.250	8.022	11.983	9.142	4.571
7	3.500	14.549	3.750	9.951	17.037	11.088	5.544
8	4.000	20.093	4.250	11.907	23.070	13.055	6.528
9	4.500	26.621	4.750	13.879	30.090	15.035	7.517
10	5.000	34.138