§3. Метод касательных (метод Ньютона).

Метод касательных, связанный с именем Ньютона, является одним из наиболее эффективных численных методов решения уравнений. Идея метода очень проста. Предположим, что функция , имеющая корень на отрезке , дифференцируема на этом отрезке и ее производная не обращается на нем в ноль. Возьмем произвольную точку и запишем уравнение касательной к графику функции в этой точке

.

График функции и ее касательной близки около точки касания, поэтому естественно ожидать, что точка пересечения касательной с осью будет расположена недалеко от корня (см. рис. 2). Для определения точки имеем уравнение

,

согласно которому

.

Повторим проделанную процедуру: напишем уравнение касательной к графику функции в точке и найдем для нее точку пересечения с осью (см. рис. 2):

.

Продолжая этот процесс, получим последовательность , определенную с помощью рекуррентной формулы

.

При ее исследовании, как и при исследовании последовательности метода итераций, встают два вопроса:

1. Можно ли процесс вычисления чисел по рекуррентной формуле продолжать неограниченно, т. е. будут ли эти числа принадлежать отрезку ?

2. Если процесс бесконечен, то как ведет себя последовательность при ?

При анализе этих вопросов предположим, что корень является внутренней точкой отрезка , а функция дважды непрерывно дифференцируема на данном отрезке, причем ее производные удовлетворяют неравенствам

, , .

Следует обратить внимание на то, что в неравенствах величина дает оценку модуля первой производной снизу, а величина оценку модуля второй производной сверху.

Теорема о сходимости метода касательных.

Если функция удовлетворяет сформулированным условиям, то найдется такое : , что при любом выборе начального приближения на отрезке существует бесконечная итерационная последовательность и эта последовательность сходится к корню .

В силу предположения о дифференцируемости функции и неравенстве нулю ее производной, уравнение эквивалентно на отрезке уравнению

, где ,

так что корень исходного уравнения является одновременно корнем уравнения . Исследуем возможность отыскания этого корня с помощью метода итераций.

Вычислим и оценим производную функции :

,

.

Теперь воспользуемся непрерывностью функции и ее равенством нулю в точке . Возьмем . Для данного можно указать такое : , что для всех выполняется неравенство

.

Учитывая это, получим окончательную оценку производной

, .

В соответствии с результатами предыдущего параграфа, неравенство означает, что уравнение можно решать методом итераций: при любом выборе нулевого приближения на отрезке существует бесконечная последовательность , сходящаяся к корню . Нам остается только заметить, что итерационной последовательностью для уравнения является последовательность метода касательных.

Требование близости нулевого приближения к искомому корню является существенным для метода касательных. На рис. 3 изображен график той же функции , что и на рис. 2, однако выбрано дальше от корня , чем в первом случае. В результате после первого шага получается точка , которая не принадлежит исходному отрезку и процесс построения рекуррентной последовательности обрывается. Таким образом, для правильного выбора нулевого приближения нужно еще до начала расчетов знать область локализации искомого корня . В случае необходимости ее можно уточнить с помощью нескольких шагов по методу вилки. Затруднения, связанные с предварительным исследованием уравнения, вполне окупаются высокой скоростью сходимости метода касательных.

Задача 3.

Найти приближенное значение корня уравнения методом касательных.

Рекуррентная формула метода касательных принимает в данном случае вид

.

Выберем, как и для метода итераций, в качестве нулевого приближения и подсчитаем следующие приближения. Результаты вычислений приведены в таблице 3. Мы видим, что, начиная с номера , последовательность убывает, приближаясь к корню сверху. После четвертого шага процесс «останавливается»: пятая итерация дает тот же результат. Причина этого явления заключается в следующем. Расчеты ведутся с 12 десятичными знаками. Когда погрешность оказывается меньше , становится невозможно уловить разницу между и , лежащую за пределами ошибки округления.

Таблица 3.

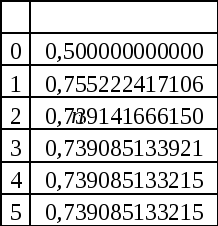
Приведенный пример показывает очень высокую скорость сходимости метода Ньютона. После двух шагов мы достигли точности . Это лучше результатов, которые мы имели в методе вилки на девятом шаге, в методе итераций – на девятнадцатом. После четырех шагов погрешность в определении корня составила .

Задача 4.

Рассмотреть вычисление как задачу решения уравнения

в области . Написать для вычисления корня уравнения итерационную последовательность по методу касательных. Вычислить с ее помощью .

Рекуррентная формула метода касательных для уравнения принимает вид

.

Она определяет монотонно убывающую последовательность, сходящуюся к сверху.

Перейдем ко второй части задания. Напомним, что . Выбирая , сделаем несколько итераций по формуле :

Третья итерация определяет с погрешностью .Расчет по формуле много проще вычисления по школьному алгоритму последовательного определения десятичных знаков.