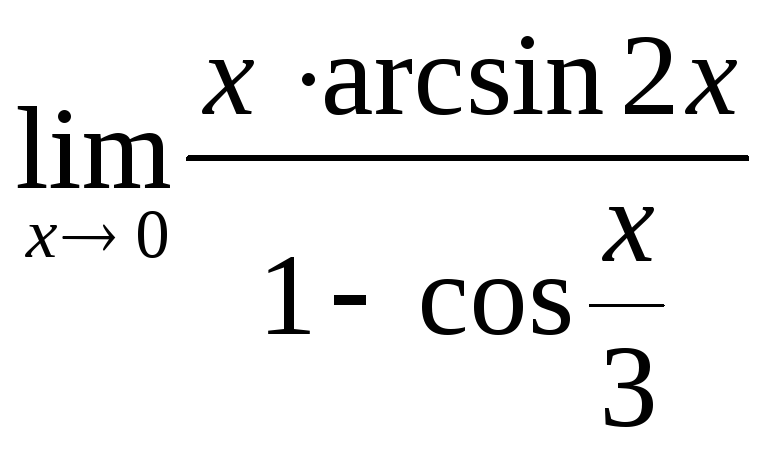- •Математика
- •Оглавление
- •Работы, выполненные без соблюдения этих правил, к зачету не принимаются и возвращаются без рецензирования для переработки. Тема 1. Функции одной переменной. Предел функции
- •Решение типовых примеров.
- •Тема 2. Производная и дифференциал функции
- •Правила дифференцирования
- •Производная сложной функции
- •Решение типовых примеров
- •Тема 3. Неопределенный интеграл
- •3. Таблица основных дифференциалов функции
- •4 Таблица интегралов.
- •5. Основные методы интегрирования.
- •Непосредственное интегрирование.
- •Замена переменной (интегрирование подстановкой).
- •Интегрирование по частям.
- •Интегрирование рациональных дробей
- •Интегрирование тригонометрических функций
- •Тема 4. Определенный интеграл.
- •Геометрический смысл определенного интеграла.
- •Задачи к теме 1. Функции одной переменной. Предел функции
- •Задачи к теме 2. Производная и дифференциал функции
- •Задачи к теме 3. Неопределенный интеграл
- •Задачи к теме 4. Определенный интеграл.
- •Список литературы
- •Приложение 1 Образец оформления титульного листа
- •Контрольная работа №2 по дисциплине «математика»
- •2011 Приложение 2 Справочный материал по элементарной математике
- •Математика
Интегрирование тригонометрических функций
Интегралы вида
![]() ,
гдеR- рациональная функция от sinxи cosx, приводятся к интегралам от
рациональных функций новой переменной
с помощью универсальной тригонометрической
подстановки
,
гдеR- рациональная функция от sinxи cosx, приводятся к интегралам от
рациональных функций новой переменной
с помощью универсальной тригонометрической
подстановки![]() .
В результате этой подстановки имеем
.
В результате этой подстановки имеем
 .
.
Задача 17. Найти
неопределенный интеграл![]() .
.
Решение.
Подынтегральная
функция является рациональной функцией
от sinxи cosx. Применяем подстановку![]() .
.

Тема 4. Определенный интеграл.
Если функция
![]() определена,
непрерывна и имеет первообразную
определена,
непрерывна и имеет первообразную![]() на отрезке
на отрезке![]() ,
то определенный интеграл находится по
формуле Ньютона-Лейбница:
,
то определенный интеграл находится по
формуле Ньютона-Лейбница:![]() ,
где
,
где![]() –
первообразная для функции
–
первообразная для функции![]() ,
то есть
,
то есть![]() ;a,b– нижний и верхний пределы интегрирования,
показывающие, как меняется переменная
интегрированиях.
;a,b– нижний и верхний пределы интегрирования,
показывающие, как меняется переменная
интегрированиях.
Формула Ньютона-Лейбница связывает определенный и неопределенный интегралы. Чтобы ею воспользоваться, следует взять сначала неопределенный интеграл, т.е. найти первообразную, причем удобно взять произвольную постоянную равной нулю: C=0, а затем вычислить разность значений этой первообразной в верхнем и нижнем пределах.
Свойства определенного интеграла




 ,
где
,
где
 –
четная
–
четная ,
где
,
где
 –
нечетная
–
нечетная
Задача 17. Найти
определенный интеграл![]() .
.
Решение.
Функция
![]() имеет
разрыв в точкахx1=1
иx2=-3, но на
отрезке
имеет
разрыв в точкахx1=1
иx2=-3, но на
отрезке![]() функция
непрерывна, а следовательно можно
применить формулу Ньютона-Лейбница.
функция
непрерывна, а следовательно можно
применить формулу Ньютона-Лейбница.
Так как
![]() ,
то используем метод замены переменной.
,
то используем метод замены переменной.
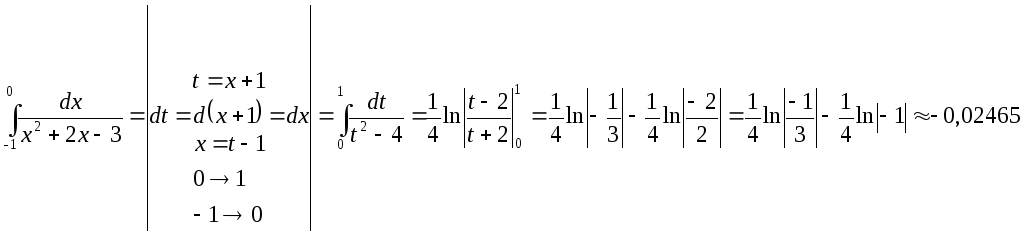
Геометрический смысл определенного интеграла.
Если непрерывная
функция
![]() неотрицательная на отрезке
неотрицательная на отрезке![]() ,
то
,
то![]() численно равен площади под кривой
численно равен площади под кривой![]() на отрезке
на отрезке![]() .
.
 yy
yy ![]()
![]()
S
S
0 a b x
0
a b
x
![]()
Задачи к теме 1. Функции одной переменной. Предел функции
Задача 1. Вычислить пределы функций, не пользуясь правилом Лопиталя.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|