5. Основные методы интегрирования.
Идея всех методов интегрирования заключается в приведении искомого интеграла к табличному интегралу или сумме табличных интегралов.
Непосредственное интегрирование.
Данный интеграл путем тождественных преобразований подынтегральной функции, применение свойств неопределенного интеграла приводится к табличному интегралу.
Задача 1. Найти
неопределенный интеграл
.
Результат проверить дифференцированием.
Решение.
Преобразуем подынтегральную функцию и применим интегралы от степенных функций:
и 
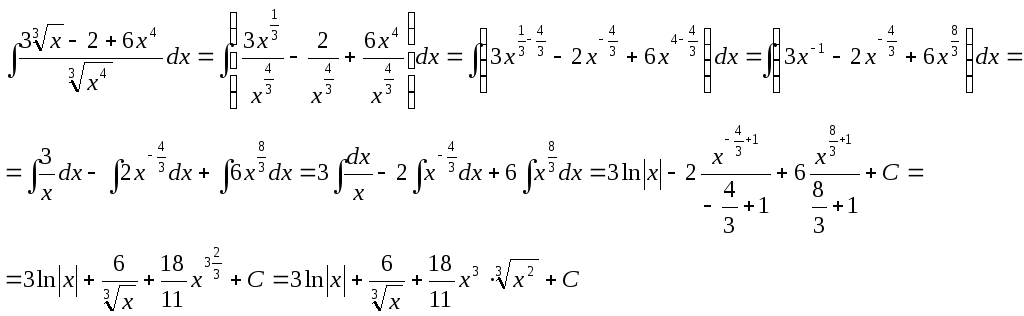Проверка.
Получена подынтегральная функция, что и требовалось показать.
Замена переменной (интегрирование подстановкой).
Сведение интеграла
к табличному виду осуществляется
введением новой переменной t
= (x).
Тогда дифференциалdtравен
.
Задача 2. Найти
неопределенный интеграл
.
Результат проверить дифференцированием.
Решение.
За новую переменную
возьмем аргумент подынтегральной
функции 
и найдемdt по
формуле:
Тогда
В последнем действии
осуществлен переход к исходной переменной
xс учетом, что
.
Проверка.
Что и требовалось показать.
Задача 3. Найти
неопределенный интеграл
.
Решение.
В
данном примере применим метод подведения
под знак дифференциала, который основан
на равенстве
.
То есть, главной задачей является
приведение подынтегральной функции к
виду
.
Поэтому желательно иметь перед глазами
таблицу производных основных элементарных
функций.
Используем метод
подведения под знак дифференциала. Из
таблицы производных имеем
,
поэтому
,
а по таблице основных интегралов видим
.
Следовательно, решение по методу
подведения под знак дифференциала будет
следующим:
Задача 4. Найти
неопределенный интеграл
.
Решение.
За новую переменную
возьмем показатель степени
.
Тогда
Задача 5. Найти
неопределенный интеграл
.
Решение.
За новую переменную удобно взять аргумент тригонометрической функции,если к тому же под интегралом присутствует производная этого аргумента (с точностью до постоянного множителя).
Задача 6. Найти
неопределенный интеграл
.
Решение.
За новую переменную удобно взять подкоренное выражение, так как под интегралом присутствует также его производная (с точностью до постоянного множителя).
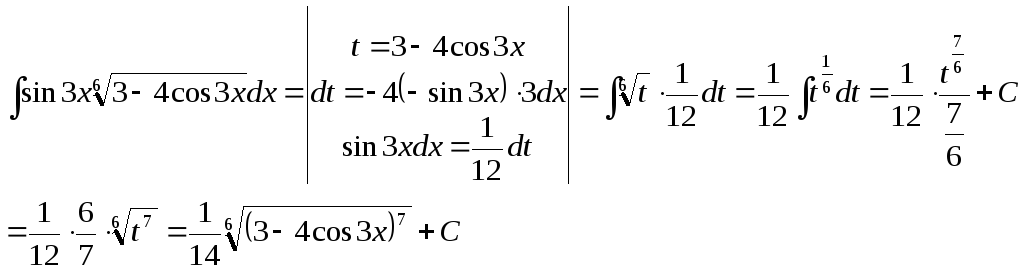
Задача 7. Найти
неопределенный интеграл
.
Решение.
За новую переменную берем функцию, стоящую в основании степени, так как подынтегральное выражение содержит производную этой функции (с точностью до постоянного множителя).
Задача 8. Найти
неопределенный интеграл
.
Решение.
Здесь под интегралом содержится логарифмическая функция,удобно принять ее за новую переменную, учитывая, что под знаком интеграла присутствует производная этой функции (с точностью до постоянного множителя).
Задача 9. Найти
неопределенный интеграл
.
Решение.
Примем за новую переменную знаменатель дроби подынтегральной функции.
Интегрирование по частям.
Интегрирование по частям производится по формуле:
Этим методом интегрируются некоторые произведения, например, произведения степенной функции на логарифмическую, или на показательную, или на тригонометрическую, или на обратные тригонометрические функции.
Чтобы воспользоваться формулой, следует один множитель в подынтегральном выражении обозначить u, а другой множитель вместе сdxпринять заdv. Для того, чтобы интеграл в правой части был проще данного интеграла, надо правильно выбрать множителиuиdv. В интегралах, берущихся по частям, обычнологарифмическую и обратные тригонометрическиефункции принимают заu, апоказательнуюилитригонометрическиефункции относят кdv.
Задача 10. Найти
неопределенный интеграл
.
Решение.
Задача 11. Найти
неопределенный интеграл
.
Решение.
Задача 12. Найти
неопределенный интеграл
.
Решение.
