
- •Курсовой проект на тему:
- •3.2. 2. Расчет гнутоклееной трехшарнирной рамы
- •Сбор нагрузок на раму
- •Значения погонных нагрузок, действующих на раму (при шаге 4,5 м)
- •Статический расчет рамы
- •Подбор сечений и проверка напряжений
- •Проверка напряжения при сжатии с изгибом
- •Проверка устойчивости плоской формы деформирования рамы
- •1. Опорный узел
- •2. Коньковый узел
- •Используемая литература
Проверка напряжения при сжатии с изгибом
Изгибающий момент, действующий в биссектрисном сечении находится на расстоянии от расчётной оси , равном :
![]() .
.
Расчетные сопротивления древесины сосны II сорта:
сжатию и изгибу:
![]()
растяжению:
![]() .
.
Здесь 15 МПа и 9 МПа – значения соответствующих расчетных сопротивлений, принимаемые по СП 64.13330.2011.
Радиус инерции сечения:
![]() .
.
При расчетной длине
полурамы
![]() ,
гибкость равна:
,
гибкость равна:
![]() .
.
Для элементов
переменного по высоте сечения коэффициент
,
учитывающий продольный изгиб, дополнительно
умножаем на коэффициент
![]() :
:
![]() ,
,
где - отношение высоты сечения опоры к максимальной высоте сечения гнутой части:
![]() .
.
Коэффициент определяем по формуле:
![]()
где
![]() – коэффициент, принимаемый для деревянных
конструкций.
– коэффициент, принимаемый для деревянных
конструкций.
Произведение
![]()
Определяем коэффициент , учитывающий дополнительный момент от продольной силы вследствие прогиба элемента, по формуле:
![]() ,
,
где
![]() −
усилию в ключевом шарнире.
−
усилию в ключевом шарнире.
Изгибающий момент по деформированной схеме:
![]() .
.
Для криволинейного
участка при отношении![]() согласно СП 64.13330.2011 прочность проверяем
для наружной и внутренней кромок с
введением коэффициентов
согласно СП 64.13330.2011 прочность проверяем
для наружной и внутренней кромок с
введением коэффициентов![]() и
и![]() к
к![]() .
.
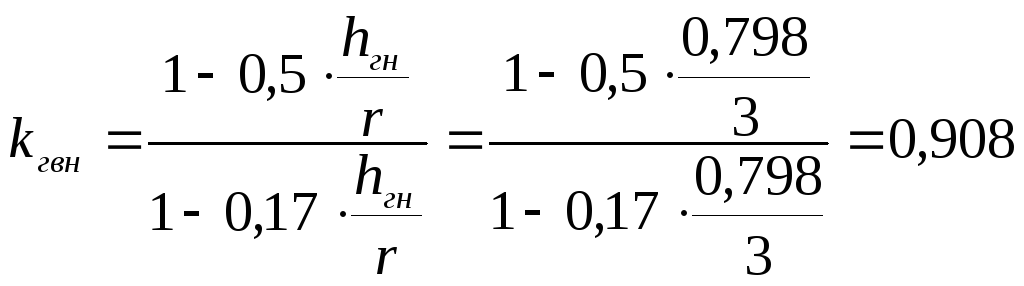 ;
;
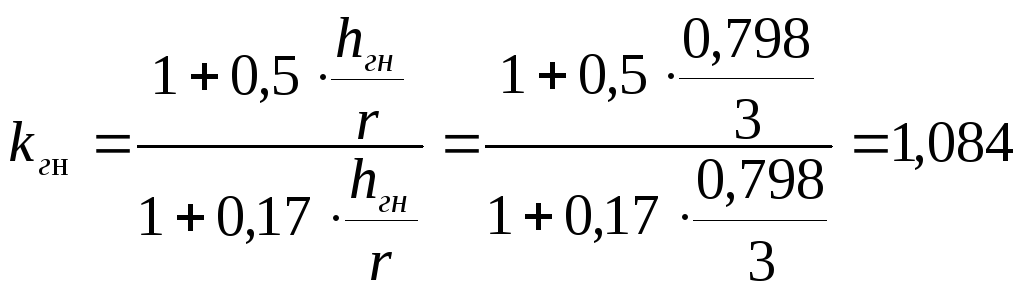 .
.
Расчётный момент сопротивления с учетом влияния кривизны:
для внутренней кромки:
![]() ;
;
для наружной кромки:
![]() ;
;
Напряжение по сжатой внутренней кромке определим по формуле:
![]() ;
;
Условие прочности по сжатию выполняется.
![]() ;
;
Недонапряжение составляет:
![]() ;
;
Условие прочности по растяжению выполняется.
![]() Принимаем:
Принимаем:
![]()
Проверка устойчивости плоской формы деформирования рамы
Рама закреплена из плоскости:
- в покрытии по наружной кромке прогонами по ригелю;
- по наружной кромке стойки стеновыми панелями. Внутренняя кромка рамы не закреплена.
Точку перегиба моментов, т.е. координаты точки с нулевым моментом находим из уравнения моментов, приравнивая его к нулю:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Расчетная длинна рамы имеет 2 участка
Первый участок:
 .
.
Второй участок:
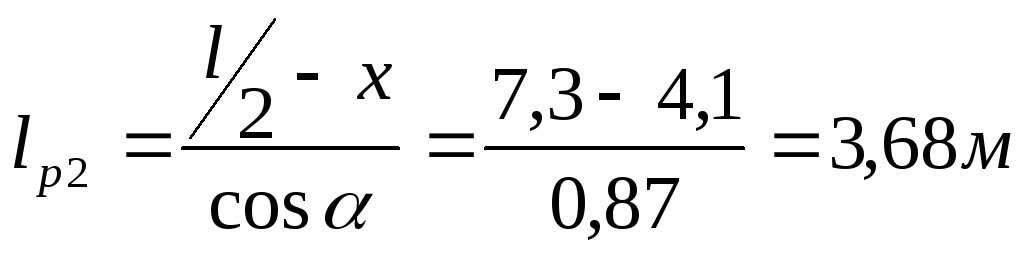 .
.
Таким образом, проверку устойчивости плоской фермы деформирования производим для 2-х участков.
Проверка устойчивости производится по формуле:
 ,
где:
,
где:
![]() –продольная сила на
криволинейном участке рамы;
–продольная сила на
криволинейном участке рамы;
![]() –изгибаемый момент,
определяемый из расчета по деформированной
схеме;
–изгибаемый момент,
определяемый из расчета по деформированной
схеме;
![]() –коэффициент
продольного изгиба, определяемый по СП
64.13330.2011;
–коэффициент
продольного изгиба, определяемый по СП
64.13330.2011;
![]() –коэффициент,
учитывающий наличие закреплений
растянутой зоны из плоскости
–коэффициент,
учитывающий наличие закреплений
растянутой зоны из плоскости
деформирования (в нашем случае n = 2, т.к. на данном участке нет закреплений растянутой зоны);
![]() –коэффициент,
определяемый по СП 64.13330.2011.
–коэффициент,
определяемый по СП 64.13330.2011.
1) Для сжатого участка
![]() находим
максимальную высоту сечения из
соотношения:
находим
максимальную высоту сечения из
соотношения:
![]() .
.
![]()
![]() .
.
Найдем значение
коэффициента
![]() по
формуле:
по
формуле:
![]()
![]()
![]() –коэффициент,
зависящий от формы эпюры изгибающих
моментов на участке
–коэффициент,
зависящий от формы эпюры изгибающих
моментов на участке
![]() определяемый по СП 64.13330.2011 (
определяемый по СП 64.13330.2011 (![]() в данном случае равен 1,13).
в данном случае равен 1,13).
![]()
Находим максимальный
момент и соответствующую продольную
силу на расчетной длине
![]() ,
при этом горизонтальная проекция этой
длины будет равна
,
при этом горизонтальная проекция этой
длины будет равна
![]()
Максимальный момент
будет в сечении с координатами:
![]() и
и![]() ;
;
![]()
![]()
![]()
![]()
Момент по деформируемой схеме:
![]() ,
,
![]() ,
,
тогда
![]() ,
,![]() .
.
Так как
![]() ,
принимаем
,
принимаем![]() ,
где
,
где![]() .
.
Коэффициент
![]() для
для![]() ,
,
тогда,
![]() ,
,
Подставим
![]() ,
,![]() .
.
При расчете элементов
переменного по высоте сечения, не имеющих
закреплений из плоскости по растянутой
кромке или при числе закреплений
![]() ,
коэффициенты
,
коэффициенты![]() и
и![]() –
следует дополнительно умножать,
соответственно, на коэффициенты
–
следует дополнительно умножать,
соответственно, на коэффициенты![]() и
и![]() в плоскости
в плоскости![]() :
:
![]()
![]() .
.
Тогда
![]()
![]()
Подставим значения в формулу:
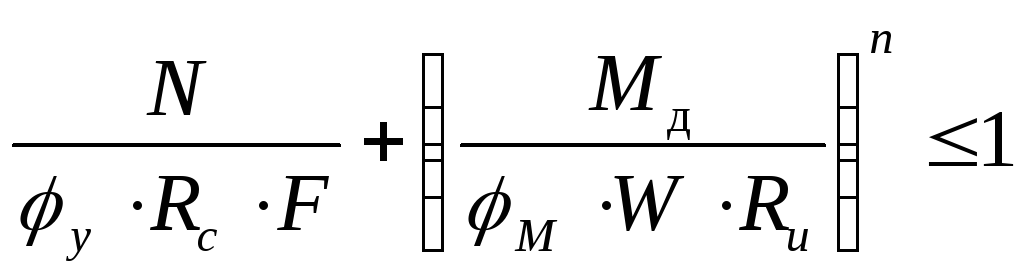
и получим:
![]()
2) Производим проверку
устойчивости плоскости формы деформирования
растянутой зоны на расчетной длине
![]() ,
где имеются закрепления растянутой
зоны.
,
где имеются закрепления растянутой
зоны.
Гибкость:
![]() ;
;
Коэффициент
![]() :
:
![]() ;
;
Коэффициент
![]() :
:
![]() .
.
При закреплении
растянутой кромки рамы из плоскости,
коэффициент
![]() необходимо умножать на коэффициент
необходимо умножать на коэффициент![]() ,
а
,
а![]() – на коэффициент
– на коэффициент![]() .
.
Поскольку верхняя
кромка рамы раскреплена прогонами и
число закреплений
![]() ,
,
величину
![]() следует принимать равной 1, тогда:
следует принимать равной 1, тогда:
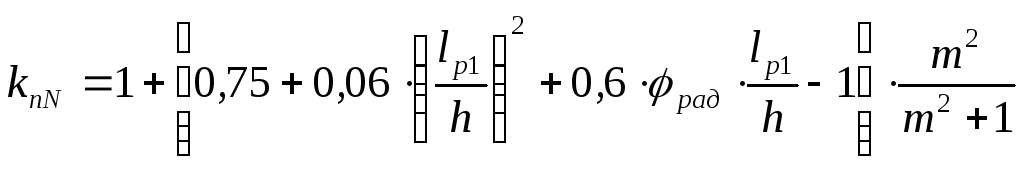 ;
;
![]() ,
где
,
где
![]() ,
– количество закрепленных точек
растянутой кромки.
,
– количество закрепленных точек
растянутой кромки.
![]() ;
;
![]() .
.
Тогда расчетные
значения коэффициентов
![]() и
и![]() примут
следующий вид:
примут
следующий вид:
![]()
![]()
Подставляя эти значения в исходную формулу проверки устойчивости плоской формы деформирования, получим:
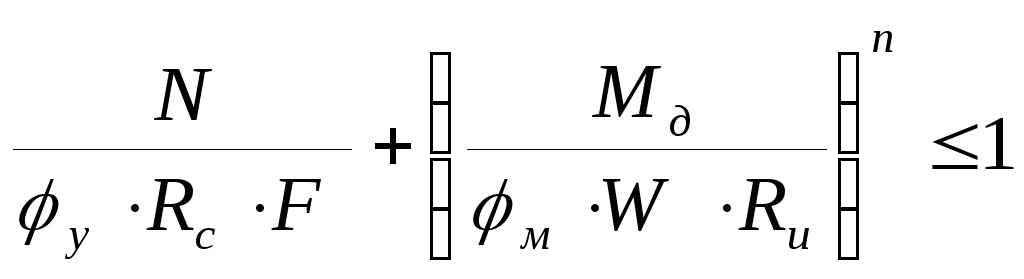
![]() ,
,
Конструкции и расчет узлов
