
- •1. Дидактическая единица № 1. Физические величины,
- •1.1. Виды и методы измерений
- •1.2. Общие сведения о средствах измерений
- •1.3. Физические величины и шкалы измерений
- •1.4. Международная система единиц си
- •2. Дидактическая единица № 2. Погрешности измерений,
- •2.1. Погрешности измерений, их классификация
- •2.2. Обработка результатов многократных измерений
- •2.3. Обработка результатов однократных измерений
- •2.4. Выбор средств измерений по точности
2. Дидактическая единица № 2. Погрешности измерений,
ОБРАБОТКА РЕЗУЛЬТАТОВ, ВЫБОР СРЕДСТВ ИЗМЕРЕНИЙ
2.1. Погрешности измерений, их классификация
71. Какими нормативными документами обеспечивается соблюдение геометрических параметров сооружения?
б) государственными стандартами Российской федерации в области строительства
72. Точность геометрического параметра – это
б) степень приближения действительного значения геометрического параметра к его номинальному значению.
73. Расчет точности обеспечивает
в) собираемость конструкций с заданными эксплуатационными свойствами при наименьших затратах
74. Цена деления шкалы измерительного прибора – это
г) разность значений измеряемой величины, соответствующая двум соседним отметкам
75. При определении ... погрешность измерительного средства является незначительной по сравнению с другими погрешностями
г) геометрических параметров теодолитом
76. При измерении усилия динамометр показывает 2000 Н, погрешность градуировки равна 10 Н. Среднее квадратическое отклонение показаний F = 2 Н. Укажите доверительные границы для истинного значения измеряемого усилия с вероятностью P = 0,98 (tP = 3,143).
в) F = 2010 ± 6 Н, Р = 0,98
77. В основе определения предела допускаемой погрешности измерения лежит принцип
а) пренебрежимо малого влияния погрешности измерения на результат измерения
78. Совокупность действий, производимых с целью оценки погрешности средств измерений и установления их пригодности называется
б) проверкой
79. При числе наблюдений более 20 для оценки грубых промахов приме-
няют критерий
б) трех сигм
2.2. Обработка результатов многократных измерений
80. При числе наблюдений менее 20 для оценки грубых промахов приме-
няют критерий
а) Романовского
81. Среднее квадратическое отклонение определяется по формуле

82. Границы доверительного интервала, в котором с заданной вероятностью находится случайная погрешность среднего арифметического, определяются по формуле

83. По какой формуле определяют критерий Романовского:

84. При определении критерия трех сигм решают неравенство

85. При измерении расстояний между осями болтовых отверстий L получены значения в миллиметрах: 5003; 5001; 5000; 5001; 4999; 5002; 4998. Укажите доверительные границы условноистинного значения длины с вероятностью Р = 0,95 (tp = 2,77)
а)
L = 5001 мм, Р = 0,95
мм, Р = 0,95
Решение.
За результат многократного измерения
принимают среднее арифметическое
результатов наблюдений х. Доверительные
границы случайной погрешности результата
измерения

Среднее квадратическое отклонение погрешности измерения определяется по формуле

При многократном измерении сначала определяется среднее значение
 =
(5003 + 5001+ 5000 + 5001+ 4999 + 5002+ 4998) / 7 = 5001.
=
(5003 + 5001+ 5000 + 5001+ 4999 + 5002+ 4998) / 7 = 5001.
Среднее квадратическое отклонение погрешности измерения определяется по формуле [2]

86. Среднее арифметическое 54,3. Среднее квадратическое отклонение среднего арифметического 0,30. Границы доверительного интервала при производстве 6 измерений с обеспеченностью 0,95 см. таблицу.
а)
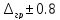
Решение. Доверительные границы случайной погрешности результата измерения определяются по формуле

где
 –значение
функции Стьюдента;
–значение
функции Стьюдента;
 –среднее
квадратическое отклонение среднего
арифметического.
–среднее
квадратическое отклонение среднего
арифметического.
В
соответствии с таблицей коэффициент
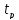 при вероятности 0,95 и 6 измерениях равен
2,57
при вероятности 0,95 и 6 измерениях равен
2,57
 =
±2,57 · 0,30 = ±0,8
=
±2,57 · 0,30 = ±0,8
87. Среднее квадратическое отклонение среднего арифметического определяется по формуле …, где
х – среднее арифметическое измеряемой величины;
х – значение физической величины; n – количество наблюдений;
m – количество пар наблюдений.

88. Определите условно-истинное значение расстояния между осями L колонн и доверительный интервал, в котором находится это значение с вероятностью Р = 0,99 (tp = 4,6). Измеренное расстояние в метрах: 17,153; 17,154; 17,150; 17,149; 17,152. Среднее квадратическое отклонение среднего арифметического 0,89
а) L = 17151 4 мм, Р = 0,99
Решение. Условно-истинное значение расстояния между осями с определенной степенью вероятности можно записать как
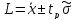

В условиях задачи оно определено и равно 0,89. Доверительный интервал:
4,6 · 0,98 = 4,09 = 4 мм. Условно-истинное значение L = 17151 4 мм.
