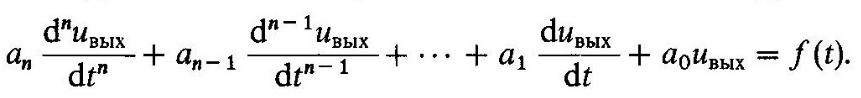
Системы, описываемые дифференциальными уравнениями
Предположим, что входной сигнал uBX(t) задан. Тогда правая часть уравнения, которую можно условно обозначить 
, является известной функцией. Анализ поведения системы сводится при этом к хорошо изученной в математике проблеме решения линейного дифференциального уравнения n-го порядка с постоянными коэффициентами:
Порядок n этого уравнения принято называть порядком динамической системы.
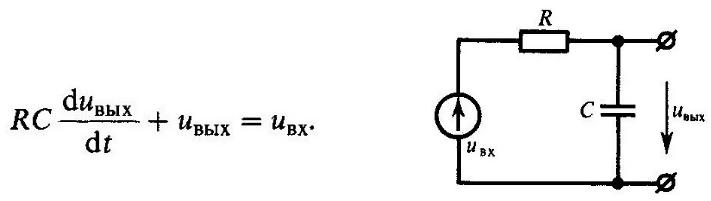
Пример 3
Дана RC-цепь вида Г-образного четырехполюсника, возбуждаемая со стороны входа источником ЭДС um(t). Выходным сигналом служит напряжение на конденсаторе.
Поскольку ток в цепи 
то используя второй закон Кирхгофа, получаем дифференциальное уравнение
RC-цепь служит примером динамической системы 1-го порядка. Важнейший параметр этой цепи — постоянная времени 
= RC, определяющая характерный временной масштаб протекания процессов в системе.
Пример 4
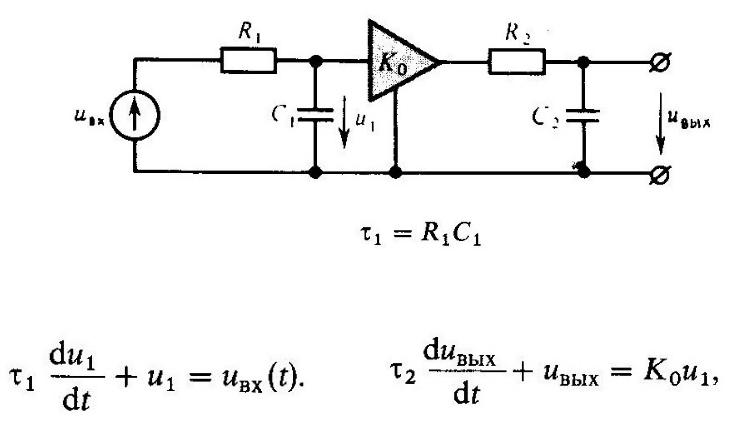
Дана более сложная система, образованная двумя RC-цепями, которые разделены идеальным усилителем с коэффициентом усиления Ко.
Входное сопротивление усилителя неограниченно велико, а выходное сопротивление бесконечно мало, поэтому усилитель является идеальным элементом развязки между цепями.
Вводя две постоянные времени и 
по аналогии с предыдущим примером имеем следующие дифференциальные уравнения 1-го порядка:
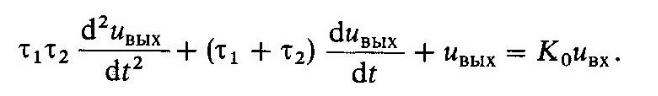
Пример 4. Продолжение
Исключив отсюда вспомогательную величину и1, получаем дифференциальное уравнение цепи:
Рассмотренная здесь более сложная RC-цепь оказывается уже системой 2-го порядка.
Пример 5
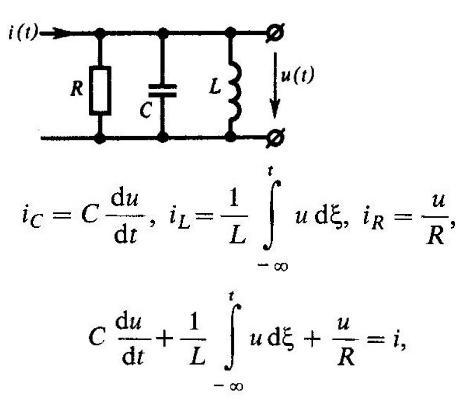
Найти дифференциальное уравнение параллельного колебательного контура с потерями, считая, что входным сигналом служит ток i(t), а выходным сигналом является напряжение u(t) на контуре.
Суммируя токи
получаем уравнение
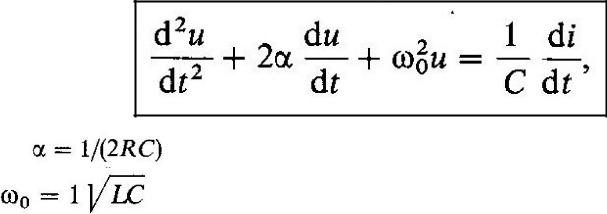
Пример 5. Продолжение
которое путем однократного дифференцирования по времени приводится к виду
где |
— коэффициент затухания контура, |
|
— частота собственных колебаний в контуре без потерь. |
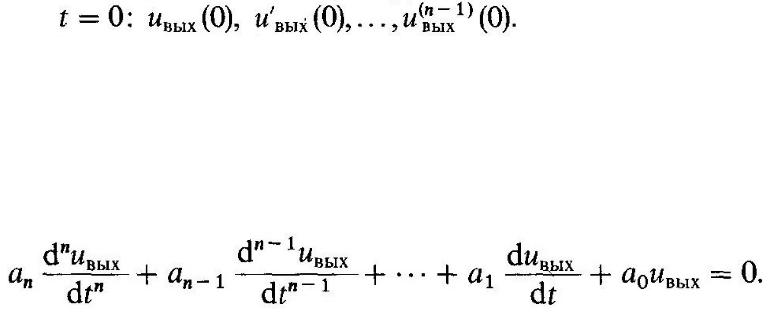
Собственные колебания динамических систем
Чтобы полностью определить поведение динамической системы, описываемой дифференциальным уравнением, требуется учесть начальные условия, которые характеризуют внутреннее состояние системы в некоторый фиксированный момент времени.
Обычно принято задавать искомую функцию и ее n - 1 производную при
Из теории дифференциальных уравнений известно, что решением дифференциального уравнения, удовлетворяющим любым начальным условиям, является сумма некоторого частного решения неоднородного уравнения, у которого правая часть f(t) отлична от нуля, и общего решения однородного уравнения
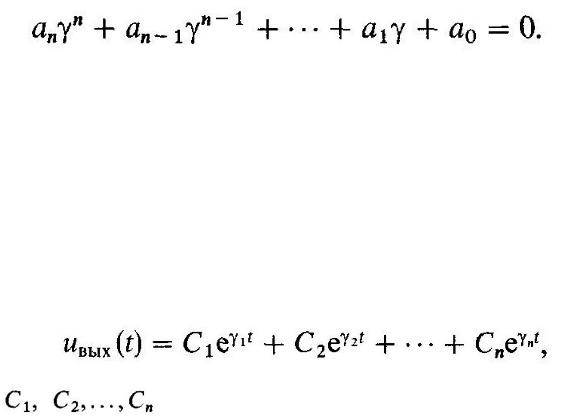
Собственные колебания динамических систем
Проблема решения однородного дифференциального уравнения связана с нахождением корней характеристического уравнения системы
Данное уравнение имеет ровно n корней. Поскольку коэффициенты уравнения вещественны, корни 
могут быть либо вещественными, либо комплексно-сопряженными. Если все корни различны, то общее решение однородного уравнения, которое описывает
собственные колебания системы, имеет вид
где |
— постоянные числа, определяемые из начальных |
условий. |
|
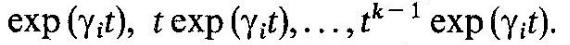
Собственные колебания динамических систем
Если же некоторые из корней оказываются кратными, то составляющие общего решения однородного уравнения несколько усложняются за счет появления секулярных (вековых) множителей. Так, если 
представляет собой k-кратный корень, то ему отвечает совокупность собственных колебаний вида
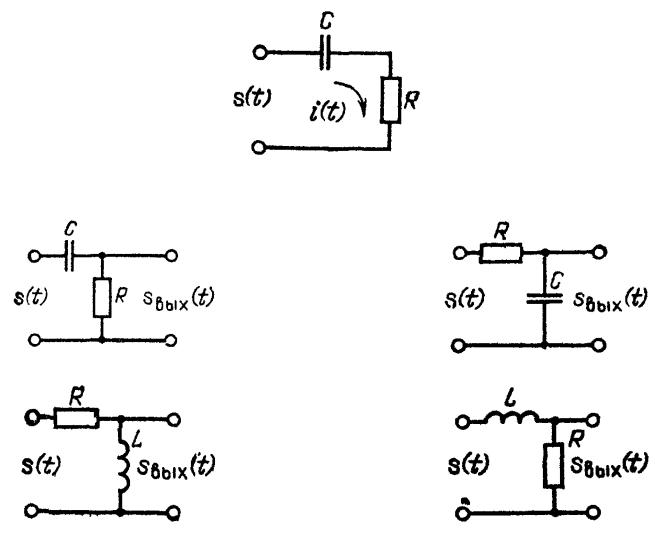
Дифференцирование и интегрирование сигналов
Простейшая цепь, используемая для дифференцирования или интегрирования
Дифференцирующие цепи |
Интегрирующие цепи |