РАДИОТЕХНИЧЕСКИЕ
ЦЕПИ И СИГНАЛЫ
Лекционный курс Лекция 9
Доцент Трухин М.П.
Угловые колебания при сверхбольших индексах модуляции
Принцип линейной частотной модуляции (ЛЧМ)
Рассмотрим радиоимпульс с огибающей прямоугольной формы. Будем полагать, что частота заполнения линейно нарастает от начала импульса к его концу. Конкретизируя математическую модель сигнала, предположим, что его длительность равна 
причем точка t = 0 соответствует середине импульса, а мгновенная частота изменяется во времени по закону
Здесь — несущая частота; — параметр с размерностью с-2, равный скорости изменения частоты во времени.
За время, равное длительности импульса, девиация частоты
Полная фаза сигнала
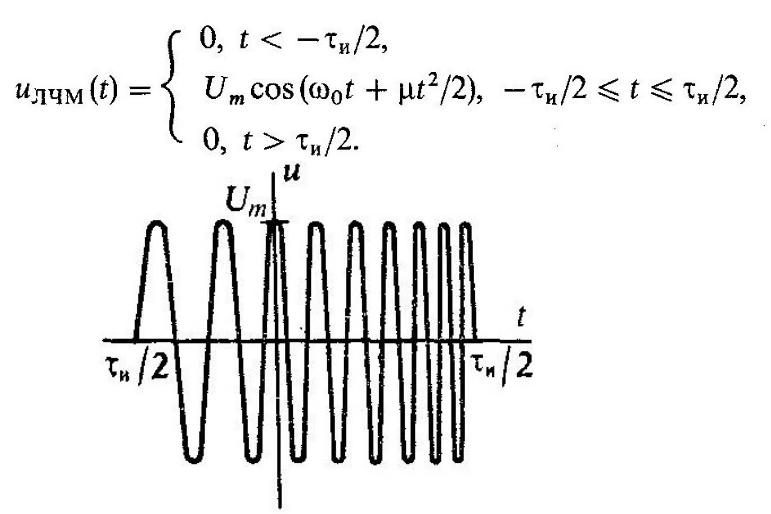
ЛЧМ-сигнал
Радиоимпульсом с линейной частотной модуляцией, или ЛЧМ-импульсом, называется сигнал, представляемый следующей математической моделью:
Свойства ЛЧМ-сигнала
Замечательное свойство ЛЧМ-сигналов, определяющее их практическую значимость, состоит в следующем.
Предположим, что имеется некоторое физическое устройство, осуществляющее задержку сигналов, подаваемых на его вход. Если время задержки зависит от частоты сигнала, причем с ростом частоты это время уменьшается, то при определенных условиях, подавая на вход такого устройства ЛЧМ-импульс большой длительности, можно добиться существенного «сжатия» его во времени.
Этот эффект обусловлен тем, что на выходе устройства задержки одновременно будут появляться составляющие как более низкочастотные, относящиеся к началу импульса, так и более высокочастотные, наблюдаемые в его конце.
Спектр прямоугольного ЛЧМ-импульса
Спектр такого сигнала имеет сложную структуру из-за перекрестного влияния отдельных спектральных составляющих.
На основании математической модели запишем выражение спектральной плотности одиночного ЛЧМ-импульса:
Спектр прямоугольного ЛЧМ-импульса
Первый интеграл описывает часть спектральной плотности с резко выраженным максимумом в области положительных частот, близких к Второй интеграл соответствует части спектральной плотности, сосредоточенной в основном при 
На практике интересуются исключительно случаем, когда эффект перекрытия спектров, концентрирующихся при положительных и отрицательных частотах, пренебрежимо мал. Это связано с тем, что полная девиация частоты за время длительности импульса очень мала по сравнению с несущей частотой:
Поэтому в формуле следует вычислять только первый интеграл, дающий спектральную плотность при 
Спектр в области отрицательных частот может быть получен на основании свойств преобразования Фурье для вещественных сигналов
Спектр прямоугольного ЛЧМ-импульса
Дополнив аргумент экспоненциальной функции в формуле до полного квадрата, получим
Удобно перейти от переменной t к новому аргументу х, выполнив замену переменной:
Спектр прямоугольного ЛЧМ-импульса
Проводя вычисления, находим
где пределы интегрирования определяются следующим образом:
Интеграл в выражении сводится к комбинации хорошо изученных специальных функций — интегралов Френеля:
Спектр прямоугольного ЛЧМ-импульса
В результате получаем окончательную формулу для спектральной плотности ЛЧМ-сигнала:
Представив эту спектральную плотность в показательной форме:
можно заметить, что модуль (амплитудный спектр)
в то время как фазовый спектр состоит из квадратичного слагаемого 
и остаточного члена