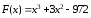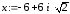6.4.3 Изменение формата графиков

Для изменения размеров рисунка нужно подвести указатель линии к маркерам изменения размера.

Эти маркеры имеют вид маленьких черных прямоугольников.

Указатель при этом приобретает форму двухсторонней стрелки, указывающей, в каких направлениях можно изменить размер рисунка.

Нажав левую кнопку мыши и захватив соответствующую сторону или угол шаблона рисунка, можно не отпуская кнопки, растягивать или сжимать шаблон.

После того как кнопка будет отпущена, размер рисунка изменится.

Сжимать и растягивать графики можно в вертикальном, горизонтальном и диагональном направлениях.

Если при выделенном рисунке нажать клавишу F3, Рис. будет перенесен в буфер обмена. Переместив курсор в новое место и нажав клавишуF4, можно вставить Рис. в новое место.

Обширные возможности форматирования графиков дает окно форматирования, которое появляется, если дважды щелкнуть мышью на графике.

6.4.4 Правила трассировки графиков

Если щелкнуть в области графика правой кнопкой мыши, появляется меню. В нем есть команда Tracy(трассировка). Эта команда выводит окно трассировки двумерных графиков, представленное на рис. 4.4.

Рис.6.29 Трассировка двумерных графиков

Трассировка начинает работать после выделения графика и позволяет определить значение функции в любой точке графика. В окне графика появляется большое перекрестие из двух черных пунктирных линий. С помощью указателя мыши его можно перемещать по графику, устанавливая любое значение аргумента. При этом координаты точки графика, на которую установлено перекрестие, отображаются в окне трассировки.

6.4.5 Правила просмотра участков двумерных графиков

Некоторые графики представляют собой довольно сложные кривые. Для детального просмотра любого участка графика следует выделить график, поместить в него указатель мыши и щелкнуть правой клавишей. В появившемся контекстном меню следует выбрать команду Zoom(масштаб). Это ведет к открытию диалогового окнаX-YZoom, с помощью которого можно увеличить любой участок графика. Для того, чтобы воспользоваться этим окном, необходимо предварительно выделить фрагмент графика функции (рис. 6.30).

Рис.6.30 Просмотр участков

При этом в окне просмотра отображаются минимальные и максимальные значения XиY, определяющие область просмотра.

Кнопки Zoom,Unzoom,FullViewпозволяют увеличить выделенную часть графика, снять выделение и вернуться к просмотру всего графика.

5.

Определение корней алгеброических уравнений

Пусть требуется решить уравнение с одним неизвестным x:

F(x) = 0 (6.1)

Это означает найти значения x_i, называемые корнями или решениями, удовлетворяющие уравнению (6.1).

Правильность полученного решения можно проверить подстановкой.

Уравнение (6.1) называется алгебраическим уравнением n-ой степени если оно представляет собой многочлен степени n относительно x:

, (6.2)

где коэффициент a_i – действительные или комплексные числа.

Алгебраической уравнение n-ой степени имеет n корней.

Алгебраическое уравнение называется действительным, если все его коэффициенты a_i – действительные числа.

Комплексные корни алгебраического уравнения могут быть только парными, комплексно сопряженными числами.

Уравнение нечетной степени всегда имеет хотя бы один действительный корень.

Аналитические методы решения уравнения (6.2) при n ≥ 3 весьма трудоемки. Компьютерные методы предельно упрощают эту задачу.

Методы решения алгебраических уравнений в среде MathCAD

Возможны 2 способа нахождения корней уравнения (6.2) в среде MathCAD:

• с помощью методов символьной математики согласно правилу 6;

• путем обращения к встроенной функции согласно правилу 2.

Рассмотрим применение обоих методов на конкретных примерах.

Пример

Найти корни кубического уравнения:

(6.3)

Решение по правилу 6:

Открываем рабочий лист и записываем многочлен из уравнения (6.3):

Выделяем (затемняем ■) в этом многочлене в любом члене один символ – переменную x – путем протаскивания курсора.

Открываем меню «Символ», подменю «Переменные» (Variable), щелчок по опции «Вычислить» (Solve).

На рабочем листе появляется результат, записанный в форме вектора:

Решение по правилу 2:

Вновь записываем многочлен из уравнения (6.3):

Выделяем (затемняем ■) в этом многочлене в любом члене один символ переменной х – путем протаскивания курсора.

Записываем вектор коэффициентов многочлена, для чего открываем меню «Символ», щелчок по опции «Коэффициенты» (Polynomial Coefficients).

Перед вектором вставляем его имя V:= . Получаем результат:

Следует отметить, что при отсутствии какого-либо члена, соответствующий ему коэффициент принимается равным 0.

Обращаемся к пиктограмме «Встроенная функция» f(x) на второй строке текстового окна – стандартной линейке.

На появившемся после щелчка диалоговом окне в разделе «Категория функций» выбираем строку с надписью «Решение» (All), а в разделе «Название функции» – polyroots (корни полинома).

После нажатия на кнопку «ок» или «Вставить» на рабочем листе появляется название данной функции.

В скобки вписываем имя вектора коэффициентов V и вводим знак =.

После ввода знака равенства получаем результат в виде вектора:

,

Точность полученного результат устанавливаем путем открытия меню «Формат», подменю «Результат» и выбора требуемого числа десятичных знаков в открывшемся окне.

Проводим проверку полученных результатов.

Для этого последовательно при каждом из полученных значений корня x_i (переносим их методом копирования) вычисляем значение многочлена F(x).

Близость к нулю действительной и мнимой частей F(x) указывает на правильность полученных результатов:

check-up