
- •6.2.5 Управление элементами интерфейса
- •6.2.6 Выделение областей
- •6.2.7 Изменение масштаба документа
- •6.2.8 Обновление экрана
- •6.2.9 Содержание инструментальных панелей подменю «математика»
- •6.3 Основные правила работы в среде «MathCad»
- •6.3.1 Удаление математических выражений
- •6.3.2 Копирование математических выражений
- •6.3.3 Перенос математических выражений
- •6.3.4 Вписывание в программу текстовых комментариев
- •6.5 Правила вычислений в среде «MathCad»
- •6.4.1 Построение графиков в декартовой системе координат
- •6.4.2 Построение графиков в полярной системе координат
- •6.4.3 Изменение формата графиков
- •6.4.4 Правила трассировки графиков
- •6.4.5 Правила просмотра участков двумерных графиков
- •Определение корней алгеброических уравнений
- •6.7.2 Определение корней трансцендентных уравнений
- •Вычисления по циклу
- •Обработка данных
- •6.8.1 Кусочно-линейная интерполяция
- •6.8.2 Сплайн-интерполяция
- •6.8.3 Экстраполяция
- •Символьные вычисления
- •6.10.1 Стратегии одномерной оптимизации
- •6.10.2 Локальные и глобальные экстремумы
- •6.10.3 Методы включения интервалов неопределенности
- •6.10.4 Критерии оптимизации
- •5 Методы поиска экстремума функции цели
- •6.10.6 Пример записи целевой функции при синтезе фильтров
- •Программирование в среде «mathcad»
- •7.1 Обзор инструкций
- •7.1.1 Инструкция Add line
- •7.1.2 Оператор внутреннего присваивания
- •7.1.3 Условная инструкция «if»
- •7.2.1 Особенность присвоения значения функции
- •7.2.2 Общие принципы задания операторов
7.2.1 Особенность присвоения значения функции
1) Если значение присваивается функции, то в отличии от стандартного синтаксиса MathCAD, определять переменные, от которых она зависит, в скобках ее имени не нужно.
Пример:

2) присвоение значений используемым функциям и переменным может быть произведено как в самой программе, так и выше нее.
При этом если в программе произвести определение уже заданных выше величин, то они переопределяться.
В свою очередь определения, сделанные в самой программе, никак не влияют на остальной документ.
Пример:


Вводим «Add Line» требуемое количество раз:

В конце программы (блока) вводится имя той величины, которая должна быть выдана в качестве ответа (здесь Т).
Присваивать программное имя необязательно ─ можно просто поставить после нее знак « = », при этом результат будет выведен непосредственно справа от алгоритма.
После нажатия на кнопку « = » справа от алгоритма будет получено:

7.2.2 Общие принципы задания операторов
1) Что бы задать нужный оператор, необходимо использовать соответствующие команды панели «программирование».
Просто набрать оператор с клавиатуры нельзя ─ он будет воспринят системой как неизвестная функция.
Кроме того, каждый оператор программирования имеет свое сочетание «горячих клавиш», узнать которое можно, подведя курсор к соответствующей ему кнопке рабочей панели.
2) Задание комплекса условий в программных операторах можно делать по разному:
─ Можно поставить курсор в соответствующий маркер оператора, задействовать команду «Add Line» (добавить линию). В появившемся программном блоке определить условия. При таком задании условий оператор будет выполнен, если будет выполнено хотя бы одно условие из множества условий (что соответствует использованию логического оператора «или»).
─ В том случае, если оператор должен быть задействован при условии выполнения всего комплекса условий, следует использовать логическое умножение «И» панели «булевы».
18.
Чтобы создать трехмерный график, требуется нажать кнопку с изображением любого из типов трехмерных графиков на панели инструментов Graph (График) (если возникнут сложности, обратитесь к. разд. 16.2). В результате появится пустая область графика с тремя осями (рис. 16.30) и единственным местозаполнителем в нижнем левом углу. В этот местозаполнитель следует ввести либо имя z функции z(x,y) двух переменных для быстрого построения трехмерного графика, либо имя матричной переменной z, которая задаст распределение данных zx,y на плоскости XY.
Рис. 16.30. Создание трехмерного графика
Рассмотрим на простом примере функции z(x,y) и матрицы z (они заданы в листингах 16.3 и 16.4, соответственно) примеры построения трехмерных графиков различных типов, создаваемых нажатием той или иной кнопки на панели Graph (График). Еще раз отметим, что для получения графиков не требуется никакого текста, кроме введения имени соответствующей функции или матрицы в местозаполнитель.
Для графиков, задаваемых матрицами, шкалу плоскости XY приходится задавать вручную. Mathcad просто рисует поверхность, точки в пространстве или линии уровня, основываясь на двумерной структуре этой матрицы. При быстром же построении графиков имеется возможность строить их в различном диапазоне аргументов, подобно двумерным графикам.
Листинг 16.3.Функция для быстрого построения трехмерных графиков
![]()
Листинг 16.4. Матрица для отображения на трехмерных графиках

Surface Plot - график поверхности (рис. 16.31 и 16.32)
Для построения графика поверхности необходимо воспользоваться клавишей Surface Plot панели инструментов Graph и следовать указаниям, описанным выше.

Рис. 16.31. Быстрое построение графика поверхности функции (листинг 16.3)

Рис. 16.32. График поверхности, заданный матрицей (листинг 16.4)
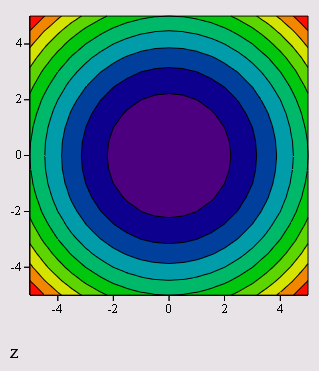
Рис. 16.33. Быстрое построение графика линий уровня функции (листинг 16.3)

Рис. 16.34. График линий уровня, заданный матрицей (листинг 16.4)
Contour Plot - график линий уровня (рис. 16.33 и 16.34)
Для построения графика поверхности необходимо воспользоваться клавишей Contour Plot панели инструментов Graph и следовать указаниям, описанным выше.
3D Bar Plot - график трехмерной гистограммы (рис. 16.35 и 16.36)
Для построения графика поверхности необходимо воспользоваться клавишей 3D Bar Plot панели инструментов Graph и следовать указаниям, описанным выше.
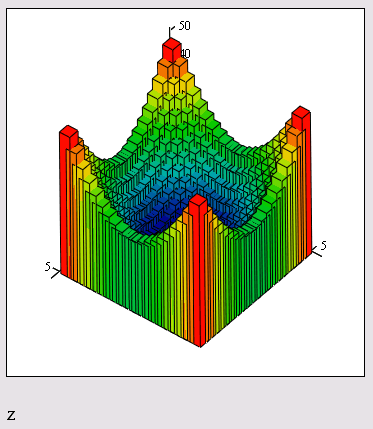
Рис. 16.35. Быстрое построение графика трехмерной гистограммы функции (листинг 16.3)

Рис. 16.36. График трехмерной гистограммы, заданный матрицей (листинг 16.4)
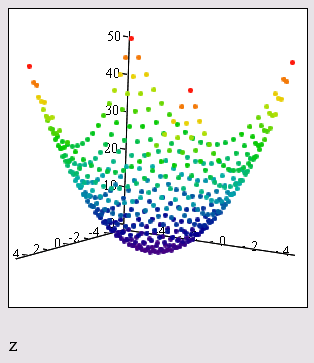
Рис. 16.37. Быстрое построение графика множества точек функции (листинг 16.3)

Рис. 16.38. График множества точек, заданный матрицей (листинг 16.4)
3D Scatter Plot - график множества точек (рис. 16.37 и 16.38)
Для построения графика поверхности необходимо воспользоваться клавишей 3D Scatter Plot панели инструментов Graph и следовать указаниям, описанным выше.
Vector Field Plot - график векторного поля (рис. 16.39)
График векторного поля несколько отличается от остальных типов двумерных графиков. Его смысл заключается в построении некоторого вектора в каждой точке плоскости XY. Чтобы задать вектор на плоскости, требуются два скалярных числа. Поэтому в Mathcad принято, что векторное поле задает комплексная матрица. Действительные части каждого ее элемента задают проекцию вектора на ось х, а мнимые — на ось у.
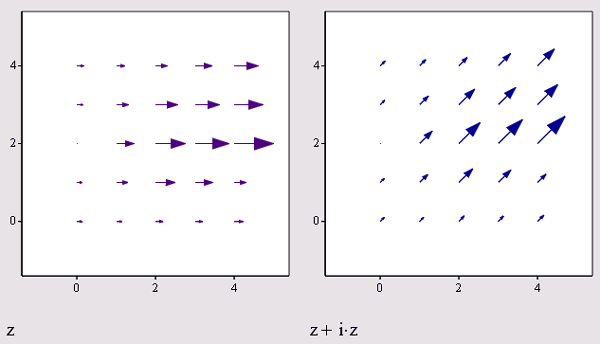
Рис. 16.39. Графики векторного поля, заданные матрицами (листинг 16.4)
Приведенные рисунки являются лишь первым шагом в создании красочных графиков. О том, как правильно отформатировать вновь созданные графики, чтобы они приобрели оптимальный с математической точки зрения и эффектный вид, рассказано в следующих разделах.
Улучшить трехмерное представление графика часто позволяет применение к исходным данным интерполяции (см. разд. "Многомерная интерполяция" гл. 15).
