Дискретная математика / 067

067

1.Какое из приведённых ниже значений является наибольшим?

1) 308 2) 110012 3) 1816 4) 1204 5) 2203

2. Определить сумму трёх чисел СА16 + 10010112 + 112

1) 11716 2) 1000110002 3) 1000110112 4) 1000110012 5) 4318

3. Ниже приведена запись процедуры вычисления разности двоичных чисел:

10011110 – 10011011

Заменить буквы А, В, С, D на цифры.

10011110 1) A=1 B=1 C=1 D=1;

+ 2) A=0 B=0 C=0 D=0;

0110010А 3) A=1 B=0 C=0 D=0;

+ 4) A=0 B=0 C=1 D=1;

0000001В 5) A=0 B=1 C=0 D=1.

+

1

------------

0CD00011

4. В записи процедуры умножения двух двоичных чисел заменить буквы A, B, C, D, E цифрами:

1111

x 1110 1) A=1 B=1 C=1 D=1 E=0;

----- 2) A=1 B=1 C=1 D=1 E=1;

0000 3) A=1 B=0 C=0 D=0 E=1;

+ A111 4) A=0 B=0 C=1 D=1 E=1;

1B22 5) A=0 B=1 C=0 D=1 E=0.

11C1

-------------

DE010010

5. Собирая грибы, три приятеля: Лёнчик, Пончик и Батончик нашли клад и, чтобы не перессориться, разделили его на 3 части. Каждый спрятал свою часть под своим деревом. Но, встретив лесника, они сбивчиво начали рассказывать о случившемся,

Лёнчик: Я спрятал клад под ёлкой, Пончик – под дубом.

Пончик: Лёнчик спрятал клад под сосной, Я – под ёлкой.

Батончик: Я спрятал клад под ёлкой, а Лёнчик – под дубом.

Наблюдательный лесник понял, что каждый из них один раз соврал и один раз сказал правду. Где каждый грибник спрятал свой клад?

Ответы:

1. Пончик – под дубом, Лёнчик – под сосной, Батончик – под ёлкой.

2. Пончик – под ёлкой, Лёнчик – под сосной, Батончик – под дубом.

3. Пончик – под сосной, Лёнчик – под дубом, Батончик – под ёлкой.

4. Поник – под сосной, Лёнчик – под ёлкой, Батончик – под дубом.

5. Пончик – под дубом, Лёнчик – под ёлкой, Батончик – под сосной.

6. Пусть А=2, В=4, С =4(целые). Вычислить значение выражения B v C A

Ответы: 1) -2; 2) 6; 3) 1; 5) 11.

7. Привести формулу к минимальной ДНФ: [(A B -> C)] -> (C <-> A v B)

8. Определить, является ли натуральное число N палиндромом, т.е. числом, которое одинаково читается справа налево и слева направо, например 121, 123474321.

9. Вычислить

S =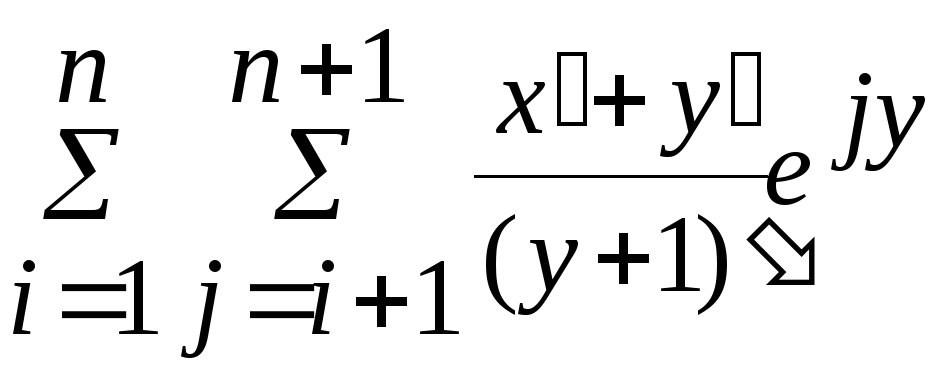

10. Какие условия из перечисленных ниже нужно использовать для попадания точки с координатами (xt, yt) внутрь заштрихованной области, показанной на рисунке? Область образована пересечением прямой, пересекающейся с осями x и y в точках (xl, 0) и (0, yl), квадратом с центром в точке (xc, yc) и диагональю 2r, и осью x.

1.abs(xt - xc)+abs(yt - yc)<r

2.abs(xt - xc)+abs(yt-yc)<2r

3.(xc*xc+yc*yc)<r*r

4.(xc*xc+yc*yc)>r*r

5.yt>-xt*yl/xl+yl

6.yt<-xt*yl/xl+yl

7.yt<-xt*yl/xk+yl

8.yt<0

9.xt<0

Ответы 1) 1 и 7 и 8 2) 2 и 6 и 8 3) 3 и 6 и 8 4) 1 и 6 и 8 5) 1 или 6 или 8

11. Опишите функцию y(x), заданную графиком.