Спец.главы математики

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

Государственное образовательное учреждение высшего и профессионального образования

«ЧИТИНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»

(ЧитГУ)

Институт переподготовки и повышения квалификации

Кафедра математики

Специальные главы математики

IV семестр

(экзамен, контрольная работа)

Тема 1 Случайные события.

Тема 2 Случайные величины.

Тема 3 Математическая статистика.

m=4

n=2

1.Случайные события.

1.1. В ящике находятся (m+3) одинаковых пар перчаток черного цвета и (n+2) одинаковых пар перчаток бежевого цвета. Найти вероятность того, что две наудачу извлеченные перчатки образуют пару.

1.2. В урне находятся 3 шара белого цвета и (n+1) шаров черного цвета. Шар наудачу извлекается и возвращается в урну три раза. Найти вероятность того, что среди извлеченных шаров окажется: а)ровно два белых шара; б) не менее двух белых шаров.

1.3. В урне находится (m+2) белых и (n+2) черных шара. Три шара последовательно извлекаются без возвращения в урну. Найти вероятность того, что третий по счету шар окажется белым.

2. Случайные величины.

2.1. Закон распределения дискретной случайной величины ξ имеет вид:

xi	-2	-1	0	m	m=n
pi	0.2	0.1	0.2	p4	p5

Найти вероятность p_4, p₅ и дисперсию Dξ, если математическое ожидание Мξ =-0,5+0,5m+0,1n..

2.2. Плотность распределения непрерывной случайной величины ξ имеет вид:

f(x)=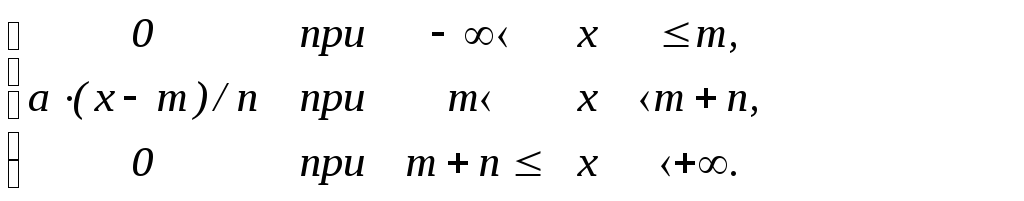

Найти:

а) параметр а; b) функцию распределения F(x);

в) вероятность попадания случайной величины ξ в интервал (m+, m+n+1);

г) математическое ожидание Мξ и дисперсию Dξ.

Построить графики функций f(x) b F(x).

3. Математическая статистика.

3.1. Численная обработка данных одномерной выборки.

Выборка X объемом N=100 измерений задана таблицей:

xi	x1	x2	x3	x4	x5	x6	x7
m	5	13	20+(m+n)	30-(m+n)	19	10	3

где x_i – результаты измерений, m - частоты, с которыми встречаются значения x_i , (), x_i=0,2ּm + (i – 1)ּ0,3ּn.

3.1.1. Построить полигон относительных частот W_i = m/N.

3.1.2. Вычислить среднее выборочное , выборочную дисперсию D_x и среднее квадратическое отклонение δ_x .