
- •Электротехника Лабораторный практикум
- •А.П. Попов, а.С. Татевосян, е.М. Завьялов, а.И. Батрак, р.Н. Хамитов
- • В.И. Степанов, а.С. Татевосян, е.М. Завьялов, р.Н. Хамитов
- •Электротехника
- •Введение
- •Лабораторная работа № 1 изучение лабораторного стенда по электротехнике
- •Краткие теоретические сведения
- •Лабораторная работа № 2 линейные электрические цепи синусоидального тока
- •Краткие теоретические сведения
- •Лабораторная работа № 3 резонанс напряжений
- •Краткие теоретические сведения
- •Лабораторная работа № 4 резонанс токов
- •Краткие теоретические сведения
- •Лабораторная работа № 5 исследование трехфазной цепи при соединении приемников электрической энергии звездой и треугольником
- •Краткие теоретические сведения
- •Лабораторная работа № 6 исследование тягового усилия электромагнита
- •Краткие теоретические сведения
- •Лабораторная работа № 7 однофазный трансформатор
- •Краткие теоретические сведения
- •Лабораторная работа № 8 трансформатор тока
- •Краткие теоретические сведения
- •Список литературы
Лабораторная работа № 2 линейные электрические цепи синусоидального тока
Цель работы. Экспериментальное исследование соотношений для токов и напряжений простейших электрических цепей синусоидального тока с катушкой индуктивностью и конденсатором.
Домашнее задание
Каковы основные характеристики синусоидального тока, напряжения и ЭДС?
Укажите угол сдвига фаз между мгновенными значениями напряжения и тока на участках цепи, содержащих резистор, катушку индуктивности и конденсатор. Какие соотношения связывают между собой мгновенные значения напряжения и тока на резистивном, индуктивном и емкостном элементах?
Как записывается комплексное сопротивление катушки индуктивности и конденсатора в алгебраической и показательной форме?
Что такое активное, реактивное и полное сопротивления электрической цепи переменного тока? Почему при прохождении тока идеальная катушка индуктивности и конденсатор не нагреваются?
Поясните понятие треугольников сопротивлений, напряжений и мощностей. Укажите коэффициенты подобия этих треугольников.
Краткие теоретические сведения
В цепи переменного
тока при подаче напряжения
![]() возникает ток
возникает ток![]() .
В неразветвленной электрической цепи
переменного тока, содержащей элементы
с параметрами: активное сопротив-лениеR,
индуктивность L
и емкость C
(рис. 1), напряжение питающей сети равно
векторной сумме напряжений, действующих
на участках цепи.
.
В неразветвленной электрической цепи
переменного тока, содержащей элементы
с параметрами: активное сопротив-лениеR,
индуктивность L
и емкость C
(рис. 1), напряжение питающей сети равно
векторной сумме напряжений, действующих
на участках цепи.
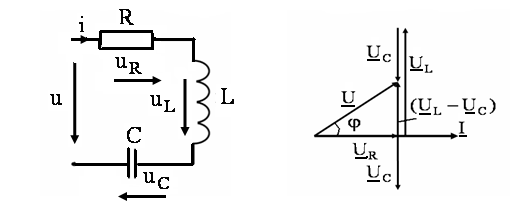
Рис. 1. Рис. 2.
В соответствии с этим выражение для напряжения, подводимого к такой электрической цепи, может быть записано по второму закону Кирхгофа в комплексной форме
![]() ,
,
где
![]() ,
,![]() ,
,![]() - комплексные напряжения на участках
цепи, определяемые как произведения
комплексного тока на соответствующие
сопротивления;R,
- комплексные напряжения на участках
цепи, определяемые как произведения
комплексного тока на соответствующие
сопротивления;R,
![]() - активное и реактивные индуктивное и
емкостное сопротивления;
- активное и реактивные индуктивное и
емкостное сопротивления;![]() - угловая частота;f
– частота напряжения.
- угловая частота;f
– частота напряжения.
По уравнению для
комплексного напряжения на входе цепи
можно построить векторную диаграмму
тока и напряжений электрической цепи.
Для этого следует помнить, что умножение
вектора напряжения на множитель (+ j)
соответствует повороту его относительно
вектора тока на угол
![]() в направлении отсчета положительных
углов (против часовой стрелки), а умножение
на множитель (-j)
– соответственно повороту вектора
напряжения на угол
в направлении отсчета положительных
углов (против часовой стрелки), а умножение
на множитель (-j)
– соответственно повороту вектора
напряжения на угол
![]() по
часовой стрелке. Вектор напряжения
по
часовой стрелке. Вектор напряжения![]() на активном сопротивлении при этом
совпадает с вектором тока
на активном сопротивлении при этом
совпадает с вектором тока![]() .
Угол
.
Угол![]() - угол между векторами тока и напряжения,
подводимого к цепи (откладывается от
вектора тока к вектору напряжения).
Векторная диаграмма для электрической
цепи (рис. 1) представлена на рис. 2.
- угол между векторами тока и напряжения,
подводимого к цепи (откладывается от
вектора тока к вектору напряжения).
Векторная диаграмма для электрической
цепи (рис. 1) представлена на рис. 2.
Уравнение для подводимого к электрической цепи комплексного напряжения с учетом его составляющих преобразуется к виду
![]()
или к виду уравнения, записанного в комплексной форме по закону Ома для всей цепи:
![]()
где
![]() -
комплексное сопротивление электрической
цепи переменного тока.
-
комплексное сопротивление электрической
цепи переменного тока.
Модуль комплексного сопротивления (полное сопротивление) цепи переменного тока
![]()
Из этого выражения следует, что полное сопротивление электрической цепи переменного тока зависит не только от параметров цепи, но и от частоты питающего напряжения, причем для линейной электрической цепи значение как полного сопротивления, так и его составляющих не зависят от подводимого напряжения.
Взаимосвязь между
действующими значениями напряжения и
полным сопротивлением цепи определяется
соотношениями
![]() или
или![]() .
.
Из треугольника
напряжений (рис. 2) можно получить
треугольник сопротивлений, разделив
стороны этого треугольника на комплексный
ток
![]() .
Из треугольника сопротивлений следует,
что
.
Из треугольника сопротивлений следует,
что
![]() .
.
Полученные выражения
показывают, что угол сдвига фаз
![]() между током
между током![]() и напряжением
и напряжением![]() питающей цепи зависит от характера
сопротивлений, включенных в цепь
переменного тока.
питающей цепи зависит от характера
сопротивлений, включенных в цепь
переменного тока.
Умножив стороны
треугольника сопротивлений на квадрат
тока в цепи
![]() ,
получим треугольник мощностей. Из
треугольника мощностей можно установить
взаимосвязь между активной
,
получим треугольник мощностей. Из
треугольника мощностей можно установить
взаимосвязь между активной![]() ,
полной
,
полной![]() и реактивной
и реактивной![]() мощностями электрической цепи. Активная
мощность цепи переменного тока
мощностями электрической цепи. Активная
мощность цепи переменного тока![]() ,
отсюда
,
отсюда![]() .
Реактивная составляющая полной мощности
цепи находится как разность реактивной
индуктивной
.
Реактивная составляющая полной мощности
цепи находится как разность реактивной
индуктивной![]() и
реактивной емкостной
и
реактивной емкостной![]() ее составляющих
ее составляющих![]() .
.
Выражение для полной мощности цепи переменного тока в комплексной форме записывают в следующем виде:
![]() или
или
![]() ,
,
где
![]() - модуль полной мощности цепи переменного
тока.
- модуль полной мощности цепи переменного
тока.
В электрических цепях переменного тока имеются также цепи с параллельным соединением потребителей электроэнергии, при котором все потребители находятся под одним и тем же напряжением. При этом на ток в цепи каждого из потребителей не влияет их количество. Значение тока в каждом из них определяется только значениями соответствующих сопротивлений и значением подводимого напряжения. Сопротивления в цепях переменного тока обычно носят комплексный характер. Пример электрической цепи переменного тока с параллельным соединением сопротивлений приведен на рис. 3.
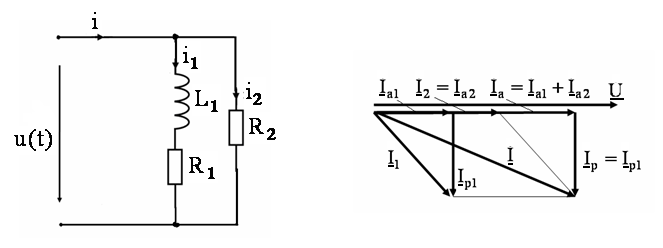
Р
Рис. 3.
Рис.
4.![]() отстает по фазе от вектора напряжения
отстает по фазе от вектора напряжения![]() на угол
на угол![]() (активно – индуктивный характер
сопротивления ветви), а вектор тока
(активно – индуктивный характер
сопротивления ветви), а вектор тока![]() совпадает по фазе вектором напряжения
совпадает по фазе вектором напряжения![]() (активный характер сопротивления ветви).
Ток
(активный характер сопротивления ветви).
Ток![]() можно
разложить на активную
можно
разложить на активную![]() и реактивную
и реактивную![]() составляющие.
составляющие.
Учитывая, что
![]() ,
,![]() и
и![]() ,
из векторной диаграммы находим:
,
из векторной диаграммы находим:
![]() ,
,
где
![]() -
активная проводимость первой ветви
электрической цепи.
-
активная проводимость первой ветви
электрической цепи.
Реактивная
составляющая тока
![]() определяется из соотношения
определяется из соотношения
![]() ,
,
где
![]() -
реактивная проводимость;
-
реактивная проводимость;![]() - реактивное сопротивление первой ветви.
- реактивное сопротивление первой ветви.
По аналогичным
соотношениям определяются активная и
реактивная составляющие тока
![]() ветви, а именно:
ветви, а именно:
![]() ,
,
![]() ,
,
где
![]() и
и![]() - соответственно активная и реактивная
проводимость второй ветви (так как
реактивное сопротивление второй ветви
- соответственно активная и реактивная
проводимость второй ветви (так как
реактивное сопротивление второй ветви![]() ,
то реактивная проводимость
,
то реактивная проводимость![]() ).
).
При этом токи в
параллельных ветвях
![]() и
и![]() будут:
будут:
![]() ;
;
![]() ,
,
где
![]() ,
,![]() - модули полных проводимостей
соответствующих параллельных ветвей.
- модули полных проводимостей
соответствующих параллельных ветвей.
Для электрической цепи с параллельным соединением сопротивлений согласно первому закону Кирхгофа для точки разветвления (узла) общий ток может быть представлен в виде векторной суммы:
![]() ,
,
где
![]() и
и![]() - комплексные токи в соответствующих
параллельных ветвях электрической
цепи.
- комплексные токи в соответствующих
параллельных ветвях электрической
цепи.
Для рассматриваемой
электрической цепи (рис. 3) можно получить
выражение для общего тока
![]() .
Определяя комплексные проводимости
.
Определяя комплексные проводимости![]() и
и![]() параллельных ветвей через комплексные
сопротивления
параллельных ветвей через комплексные
сопротивления![]() и
и![]() ,
получим
,
получим
![]() .
.
Для произвольного
числа параллельных ветвей активная
проводимость электрической цепи
![]() оказывается равной сумме активных
проводимостей всех параллельных ветвей
оказывается равной сумме активных
проводимостей всех параллельных ветвей![]() ,
а реактивная проводимость цепи равна
алгебраической сумме реактивных
проводимостей всех параллельных ветвей
,
а реактивная проводимость цепи равна
алгебраической сумме реактивных
проводимостей всех параллельных ветвей![]() .
Модуль полной проводимости цепи
определяется из выражения
.
Модуль полной проводимости цепи
определяется из выражения
![]() .
.
При этом полная
проводимость цепи также является и
величиной обратной ее полному сопротивлению
![]() .
Разделив каждый вектор
.
Разделив каждый вектор![]() тока
на векторной диаграмме (рис. 4) на вектор
напряжения
тока
на векторной диаграмме (рис. 4) на вектор
напряжения![]() ,
можно получить треугольник проводимостей
для данной цепи. В качестве примера на
рис. 5 представлен треугольник проводимостей
для первой ветви схемы (рис. 3). Из
треугольника проводимостей следует,
что
,
можно получить треугольник проводимостей
для данной цепи. В качестве примера на
рис. 5 представлен треугольник проводимостей
для первой ветви схемы (рис. 3). Из
треугольника проводимостей следует,
что![]() ,
а
,
а![]() .
С учетом этого полная
.
С учетом этого полная![]() ,
активная
,
активная![]() и
реактивная
и
реактивная![]() мощности первой ветви электрической
цепи могут быть определены через
соответствующие проводимости
мощности первой ветви электрической
цепи могут быть определены через
соответствующие проводимости
![]() ,
,
![]() ,
,![]() .
.
Полная
![]() ,
активная
,
активная![]() и реактивная
и реактивная![]() мощности второй ветви электрической
цепи определяются выражениями
мощности второй ветви электрической
цепи определяются выражениями
![]() ,
,
![]() .
.
Модуль полной мощности всей цепи при этом будет
![]() .
.
Рабочее задание
Собрать схему, приведенную на рис. 5.
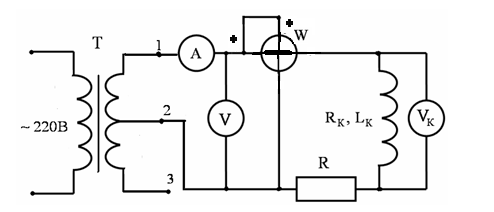
Рис. 5.
При сборке схемы использовать обмотку с индуктивностью Lк = 1,1 Гн сопротивлением обмоточного провода Rк = 160 Ом, резистор с сопротивлением R = 430 Ом. С зажимов вторичной обмотки однофазного трансформатора подать на схему переменное синусоидальное напряжение промышленной частоты f = 50 Гц.
В электрической цепи (рис. 5) произвести измерения электрических величин:
действующие значения тока
 ,
входного напряжения
,
входного напряжения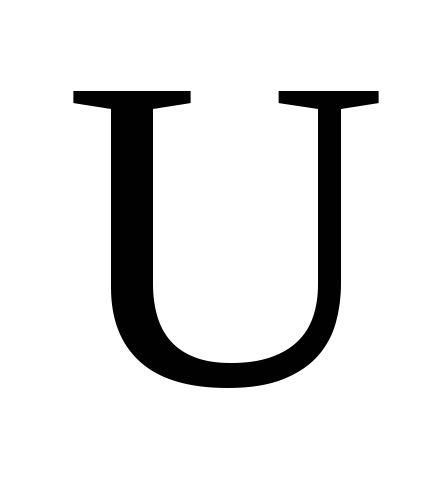 и напряжения на катушке индуктивности
и напряжения на катушке индуктивности .
Для
измерения силы тока воспользоваться
цифровым амперметром, а напряжения -
цифровым вольтметром;
.
Для
измерения силы тока воспользоваться
цифровым амперметром, а напряжения -
цифровым вольтметром; активную мощность
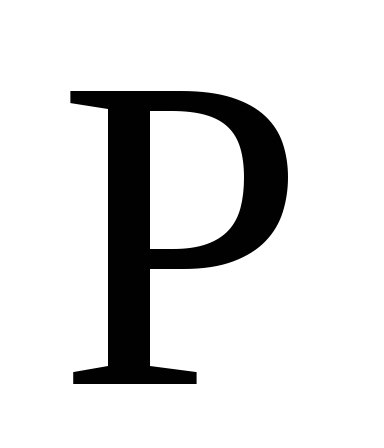 ,
потребляемую цепью, то есть среднее
значение мгновенной мощности за период
входного напряжения с помощью цифрового
ваттметра;
,
потребляемую цепью, то есть среднее
значение мгновенной мощности за период
входного напряжения с помощью цифрового
ваттметра;угол сдвига фаз
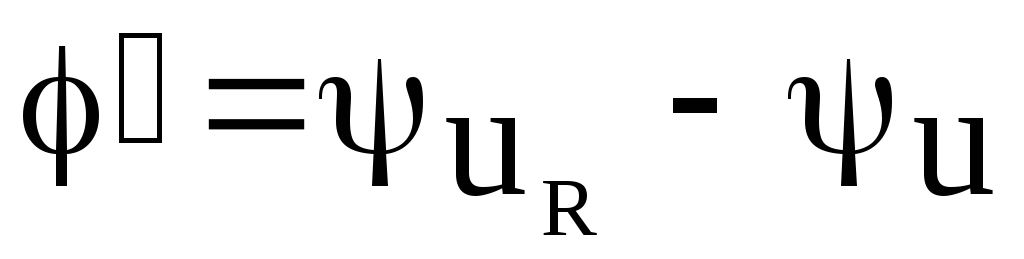 между напряжением на резисторе и входным
напряжением, переключив ваттметр на
фазометр. Угол
между напряжением на резисторе и входным
напряжением, переключив ваттметр на
фазометр. Угол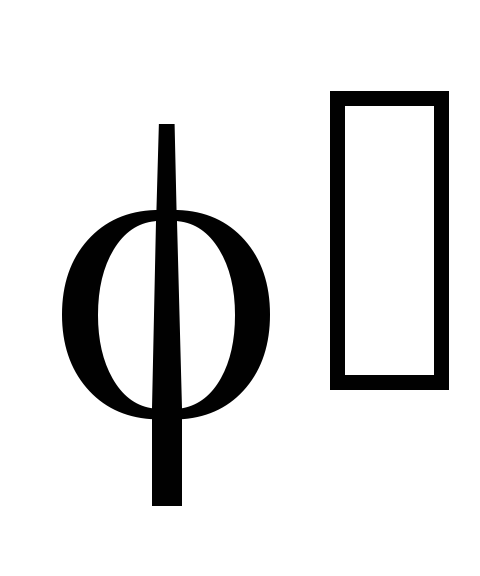 совпадает с углом сдвига фаз между
током и напряжением источника питания
совпадает с углом сдвига фаз между
током и напряжением источника питания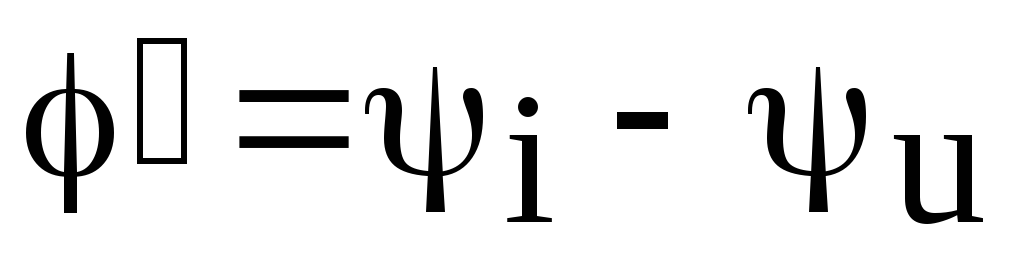 .
Поскольку аргумент
.
Поскольку аргумент комплексного сопротивления
комплексного сопротивления собранной на стенде цепи определяется
как сдвиг фаз между входным напряжением
и током
собранной на стенде цепи определяется
как сдвиг фаз между входным напряжением
и током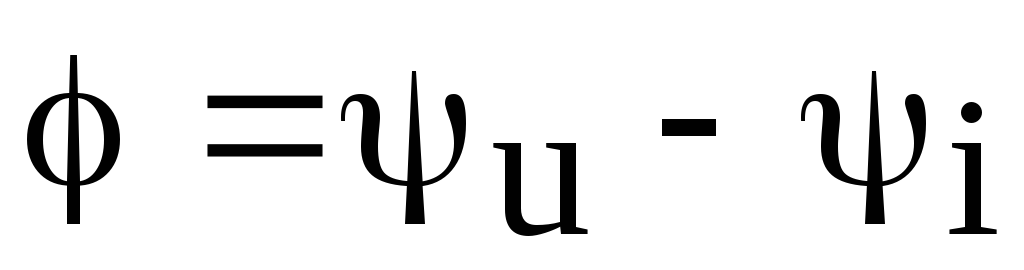 ,
то угол сдвига фаз
,
то угол сдвига фаз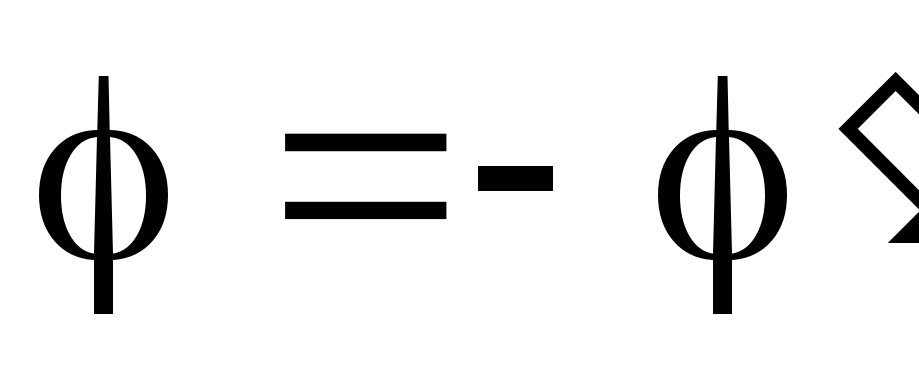 .
.
Результаты измерений занести в графу «Опыт» таблицы 1.
Таблица
1.
Опыт Расчет
U,
В
I,
мА
P,
Вт
Uк,
В
град.
URК,
В
ULК,
В
ZК,
Ом
RК,
Ом
Продолжение
таблицы 1 Расчет
XК,
Ом
RЭ, Ом
XЭ,
Ом
ZЭ,
Ом
град.
S,
ВА
Q,
вар
L,
Гн
![]() ,
,
![]() ,
,
![]()
Заполнить таблицу 1 пункта 2 рабочего задания, используя расчетные соотношения
![]()
![]()
![]()
![]()
По данным таблицы 1 пункта 3 рабочего задания построить в масштабе векторную диаграмму для электрической цепи (рис. 5).
Собрать схему, приведенную на рис.6. При сборке схемы использовать конденсатор емкостью 4 мкФ и резистор с сопротивлением R = 430 Ом.
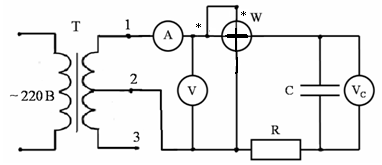
Рис. 6.
В
Таблица 2.
-
Опыт
Расчет
U,
В
I,
мА
P,
Вт
Uк,
В
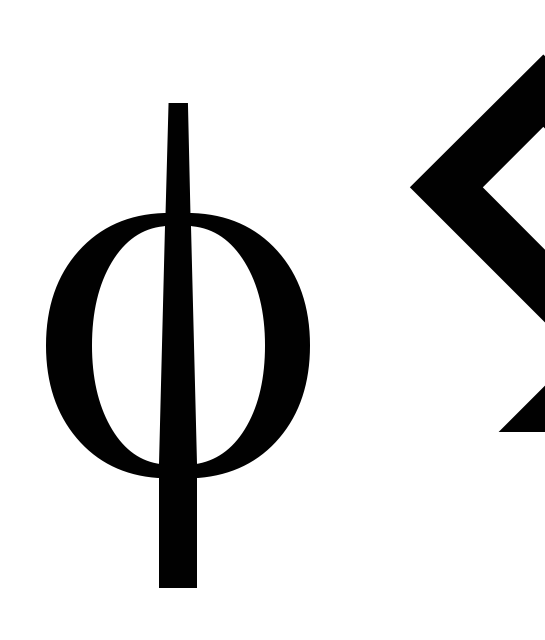 ,
,град.
Z,
Ом
R,
Ом
 ,
,град.

Продолжение таблицы 2
-
Расчет
I а ,
мА
I р ,
мА
U а ,
В
U р ,
В
G ,
Сим
B ,
Сим
S,
ВА
Q,
вар
С,
мкФ
цепи, находящейся под напряжением, произвести измерения электрических величин, аналогично пункту 2 рабочего задания. Результаты эксперимента занести в таблицу 2.-
Дополнить таблицу 2 расчетными данными, используя для определения активных и реактивных составляющих напряжений и токов соответственно в последовательной (рис. 7) и параллельной (рис. 8) эквивалентных схемах замещения цепи (рис. 6) следующие соотношения:
![]()
![]()
По данным таблицы 2 пункта 7 рабочего задания построить в масштабе векторную диаграмму для электрической цепи (рис. 6).
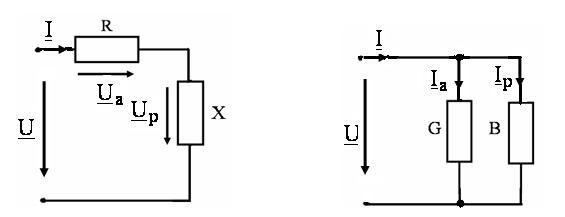
Рис. 7 Рис. 8.
Вопросы к защите
Что такое емкостное, индуктивное и комплексное сопротивления?
Как зависят реактивные сопротивления конденсатора и катушки индуктивности от частоты? Нарисуйте графики этих зависимостей.
Нарисуйте треугольники сопротивлений последовательной
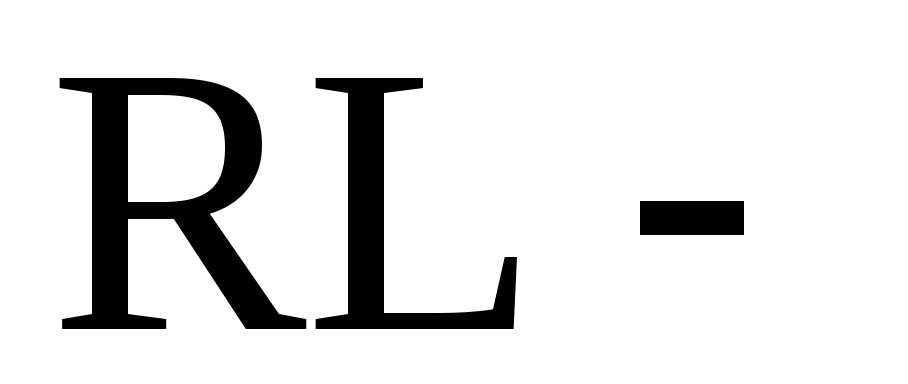 и
и
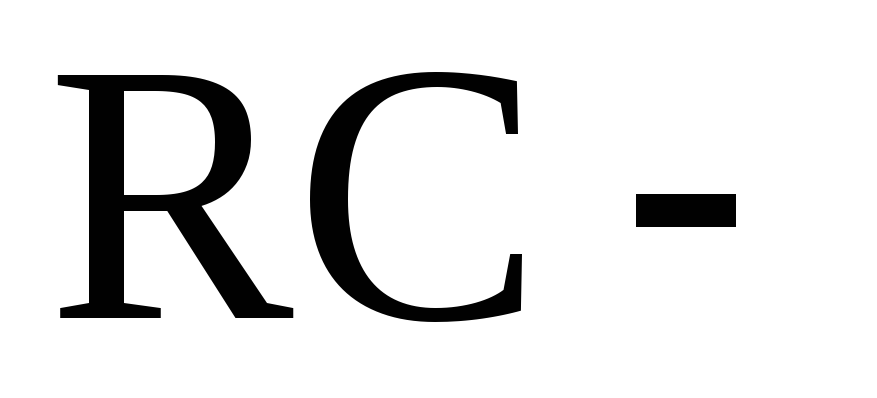 электрических цепей.
электрических цепей.
Чему равны активная, реактивная, полная и комплексная мощности в идеальных индуктивных и емкостных элементах?
Для электрической цепи (рис. 9) записать комплексы тока
 ,
напряжений
,
напряжений  и
и 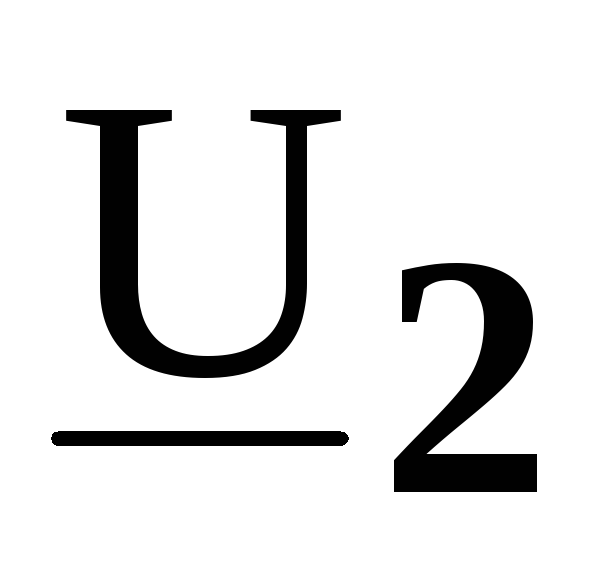 ,
если
,
если
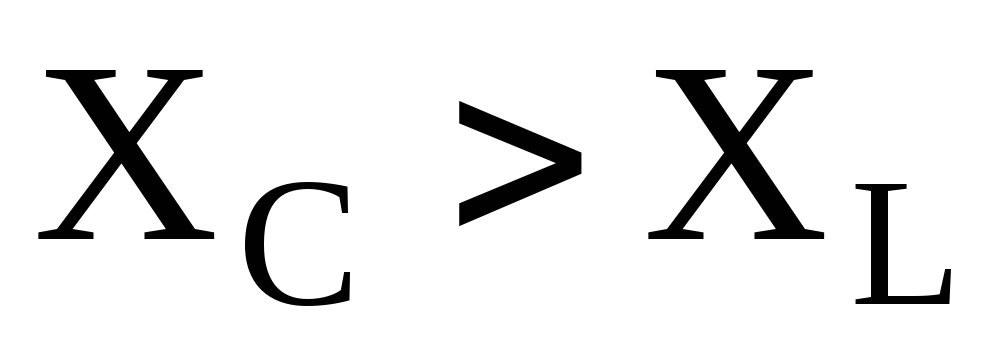 и
и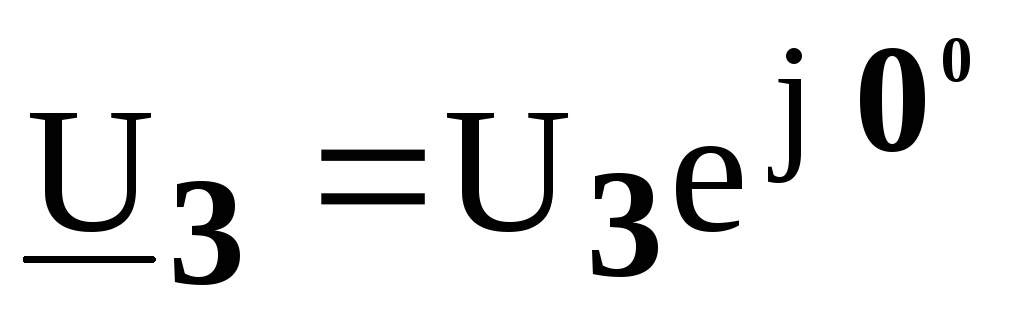 .
.
Определить по заданному входному напряжению U напряжение
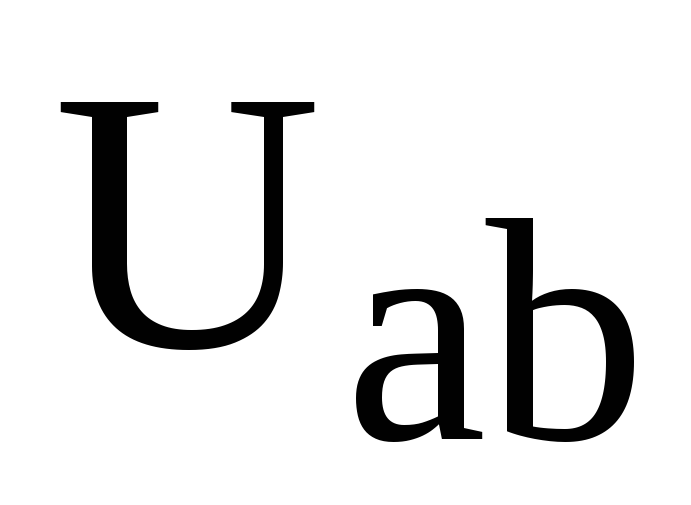 в электрической цепи (рис. 10), если
сопротивления участков
в электрической цепи (рис. 10), если
сопротивления участков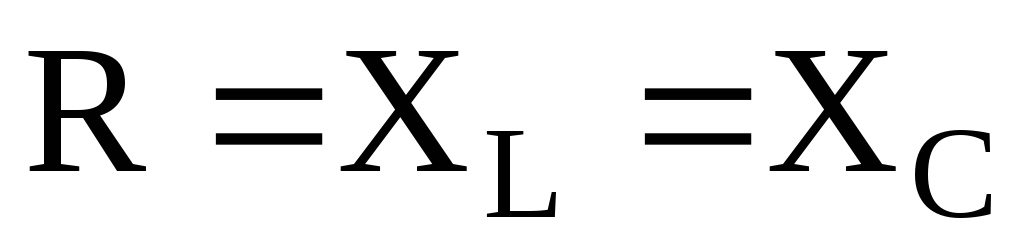 .
.
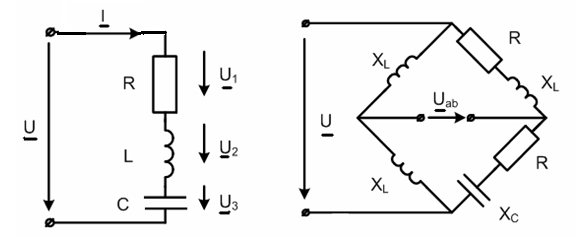
Рис. 9. Рис. 10.
По качественной временной диаграмме тока (рис. 11), проходящего через конденсатор, постройте качественные временные зависимости напряжения, мощности и энергии, запасенной в конденсаторе.
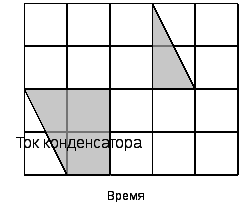
Рис. 11.
