01_Вероятность и статистика

Генеральная средняя

Пусть изучается дискретная генеральная совокупность относительно количественного признака X.

Генеральной средней называют среднее арифметическое значений признака генеральной совокупности.

Если все значения x₁, х₂, ..., х_n признака генеральной совокупности объема N различны, то

= (x₁ + х₂+ ... + x_N)/N.

Если же значения признака х₁, х₂, ..., x_k имеют соответственно частоты N₁, N₂, ..., N_k причем N₁+N₂+...+N_k=N, то

= (x₁N₁ + х₂N₂+ ... + x_kN_k)/N.

т.е. генеральная средняя есть средняя взвешенная значений признака с весами, равными соответствующим частотам.

Замечание. Если рассматривать обследуемый признак X генеральной совокупности как случайную величину, то математическое ожидание признака равно генеральной средней этого признака и наоборот:

Выборочная средняя

Пусть для изучения генеральной совокупности относительно количественного признака X извлечена выборка объема п.

Выборочной средней называют среднее арифметическое значение признака выборочной совокупности.

Если все значения x₁, х₂, ..., х_n признака выборки объема n различны, то

= (x₁ + х₂+ ... + x_n)/n.

Если же значения признака х₁, х₂, ..., x_k имеют соответственно частоты n₁, n₂, ..., n_k причем n₁+n₂+...+n_k=n, то

= (x₁n₁ + х₂n₂+ ... + x_kn_k)/n

или

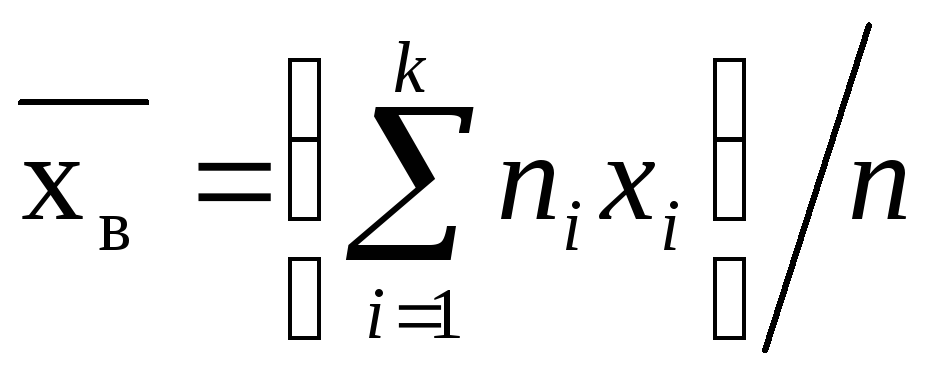
т. е. выборочная средняя есть средняя взвешенная значений признака с весами, равными соответствующим частотам.

Замечание. Выборочная средняя, найденная по данным одной выборки, есть, очевидно, определенное число. Если же извлекать другие выборки того же объема из той же генеральной совокупности, то выборочная средняя будет изменяться от выборки к выборке. Таким образом, выборочную среднюю можно рассматривать как случайную величину и говорить о числовых характеристиках ее распределения (его называют выборочным), в частности о математическом ожидании и дисперсии выборочного распределения.

Групповая и общая средние

Допустим, что все значения количественного признака X совокупности, безразлично-генеральной или выборочной, разбиты на несколько групп. Рассматривая каждую группу как самостоятельную совокупность, можно найти ее среднюю арифметическую.

Групповой средней называют среднее арифметическое значений признака, принадлежащих группе.

Общей средней называют среднее арифметическое значений признака, принадлежащих всей совокупности. Зная групповые средние и объемы групп, можно найти общую среднюю: общая средняя равна средней арифметической групповых средних, взвешенной по объемам групп.

Пример. Найти общую среднюю совокупности, состоящей из следующих двух групп:

Группа первая вторая

Значение признака ... 1 6 1 5

Частота 10 15 20 30

Объем 10+15 = 25 20+30=50

Решение. Найдем групповые средние:

;

Найдем общую среднюю по групповым средним:

Замечание. Для упрощения расчета общей средней совокупности большого объема целесообразно разбить ее на несколько групп, найти групповые средние и по ним общую среднюю.

Генеральная дисперсия

Для того чтобы охарактеризовать рассеяние значений количественного признака X генеральной совокупности вокруг своего среднего значения, вводят сводную характеристику — генеральную дисперсию.

Генеральной дисперсией D_г называют среднее арифметическое квадратов отклонений значений признака генеральной совокупности от их среднего значения .

Если все значения x₁, х₂, ..., x_N признака генеральной совокупности объема N различны, то

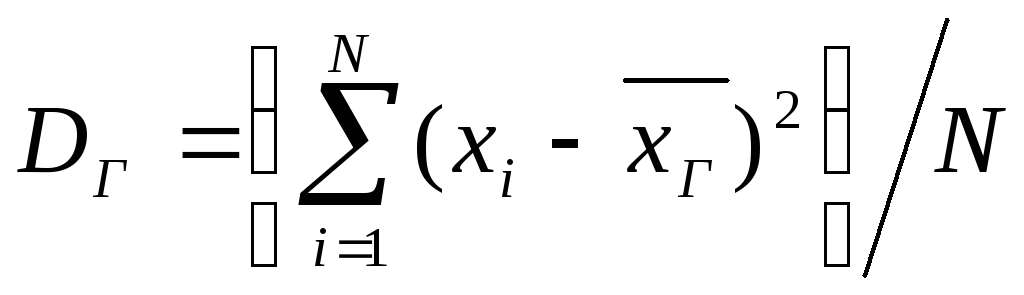
Если же значения признака х₁, х₂, ..., x_k имеют соответственно частоты N₁, N₂, ..., N_k причем N₁+N₂+...+N_k=N, то

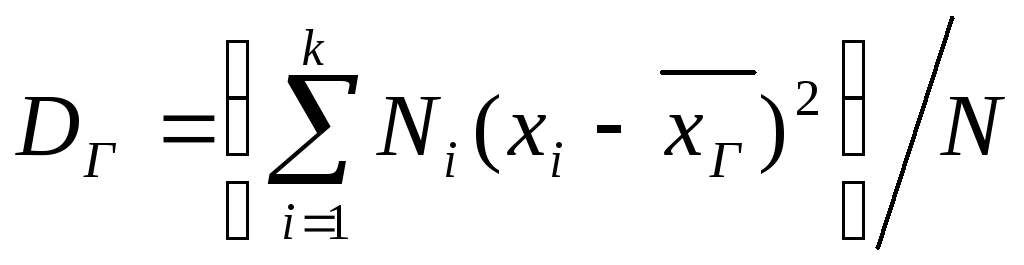
т.е. генеральная дисперсия есть средняя взвешенная квадратов отклонений с весами, равными соответствующим частотам.

Кроме дисперсии для характеристики рассеяния значений признака генеральной совокупности вокруг своего среднего значения пользуются сводной характеристикой — средним квадратическим отклонением.

Генеральным средним квадратическим отклонением (стандартом) называют квадратный корень из генеральной дисперсии:

Выборочная дисперсия

Для того чтобы охарактеризовать рассеяние: наблюдаемых значений количественного признака выборки вокруг своего среднего значения , вводят сводную характеристику — выборочную дисперсию.

Выборочной дисперсией D_B называют среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения .

Если все значения x₁, х₂, ..., x_n признака выборки объема n различны, то

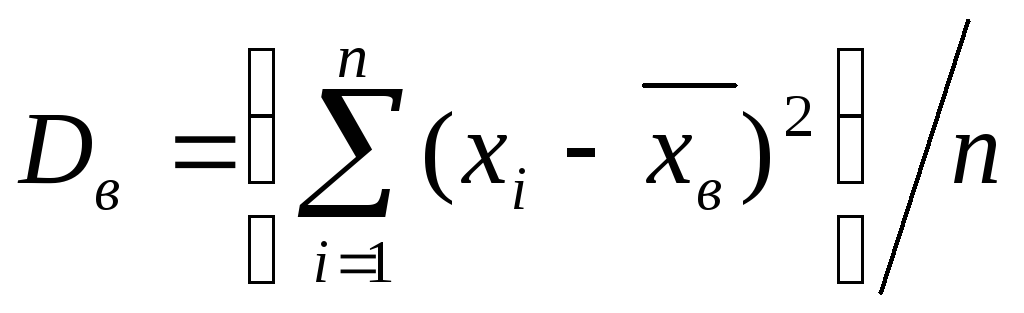
Если же значения признака х₁, х₂, ..., x_k имеют соответственно частоты n₁, n₂, ..., n_k причем n₁+n₂+...+n_k=n, то

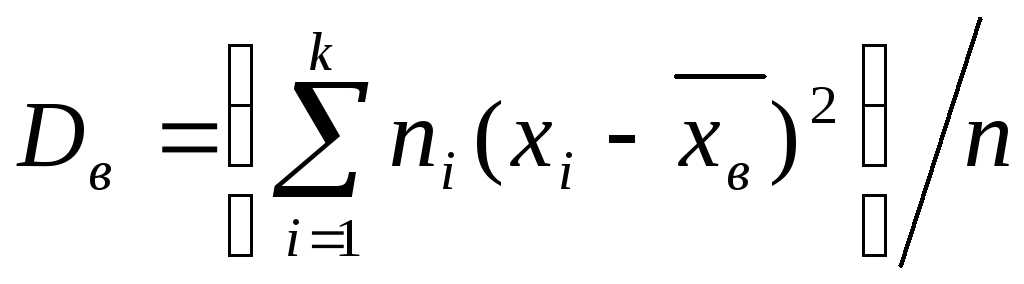
т.е. выборочная дисперсия есть средняя взвешенная квадратов отклонений с весами, равными соответствующим частотам.

По аналогии с генеральной дисперсией. Выборочным средним квадратическим отклонением (стандартом) называют квадратный корень из выборочной дисперсии:

Средняя ошибка повторной выборки – величина, выражающая среднее квадратическое отклонение выборочной средней от генеральной средней, зависит от колебемости признака в генеральной совокупности и числа отобранных единиц.

n – число отобранных единиц.

Построение нормальной кривой по опытным данным

Один из способов построения нормальной кривой по данным наблюдений состоит в следующем:

1) находят и , например, по методу произведений;

2) находят ординаты y_i (выравнивающие частоты) теоретической кривой по формуле , где п — сумма наблюдаемых частот, h — разность между двумя соседними вариантами: u_i = (x_i-)/ и

3) строят точки (x_i, y_i) в прямоугольной системе координат и соединяют их плавной кривой.

Близость выравнивающих частот к наблюдаемым подтверждает правильность допущения о том, что обследуемый признак распределен нормально.

Пример. Построить нормальную кривую по данному распределению:

варианты х_i 15 20 25 30 35 40 45 50 55

частоты n_i 6 13 38 74 106 85 30 10 4

Решение. Найдем = 34,7, = 7,38.

Вычислим выравнивающие частоты (табл. 1). Таблица 1

xi	ni	xi-	ui = (xi-)/		=248
15	6	-19,7	-2,67	0,0113	3
20	13	-14,7	-1,99	0,0551	14
25	38	-9,7	-1,31	0,1691	42
30	74	-4,7	-0,63	0,3271	82
35	106	0,3	0,05	0,3984	99
40	85	5,3	0,73	0,3056	76
45	30	10,3	1,41	0,1476	37
50	10	15,3	2,09	0,0449	11
55	4	20,3	2,77	0,0086	2
	n=366				∑yi = 366

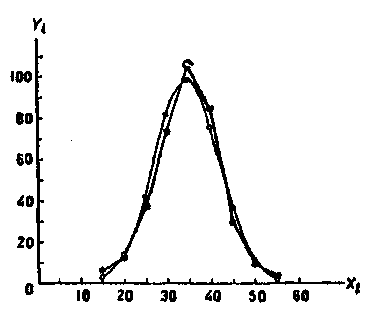
На рис. построены нормальная (теоретическая) кривая по выравнивающим частотам (они отмечены кружками) и полигон наблюдаемых частот (они отмечены крестиками). Сравнение графиков наглядно показывает, что построенная теоретическая кривая удовлетворительно отражает данные наблюдений.

Для того чтобы более уверенно считать, что данные наблюдений свидетельствуют о нормальном распределении признака, пользуются специальными правилами (критериями согласия)¹².

П Р А К Т И К А № 4

Математическая статистика.

Шифр: 123456 Исходные данные:

№	Протяженность участка, км	Коэффициент сцепления	№	Протяженность участка, км	Коэффициент сцепления
1	16872	0,4	12	3804	0,28
2	1958	0,39	13	4115	0,27
3	1771	0,38	14	13316	0,26
4	1758	0,37	15	15336	0,25
5	272	0,35	16	17255	0,24
6	1444	0,34	17	5608	0,23
7	2807	0,33	18	1441	0,22
8	11751	0,32	19	276	0,21
9	14074	0,31	20	311	0,2
10	29136	0,3	21	331	0,18
11	10021	0,29	22	298	0,17

ремонт производился на участках № 4, 7, 11, 18 и 22.

Решение:

1. Объем выборки определяется суммой частот (для каждого метра): 137630 м

2. Определяем выборочную среднюю. Т.к. варианты повторяются на определенном протяжении дороги то:

= (₁l₁ + ₂ l ₂+ ... + _k l _k)/L=

=(0,4*16872+0,39*1958+…+0,18*331)/137630=0,2958

3. Определяем величину выборочной дисперсии:

=

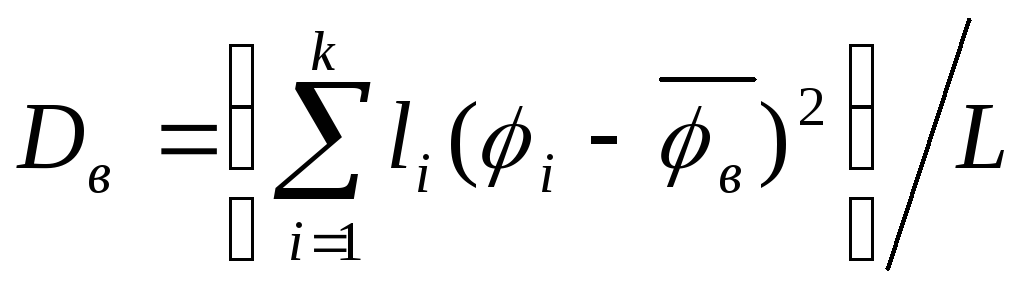=(16872*(0,4-0,2958)²+1958*(0,39-0,2958)²+…)/137630=0,0026

и стандарта (среднего квадратического отклонения):

.

4. Определяем границы коридора варьирования коэффициента сцепления:

_max=_в+t*_в=0,2958+0,0517=0,3475

_min=_в-t*_в=0,2958-0,0517=0,2441

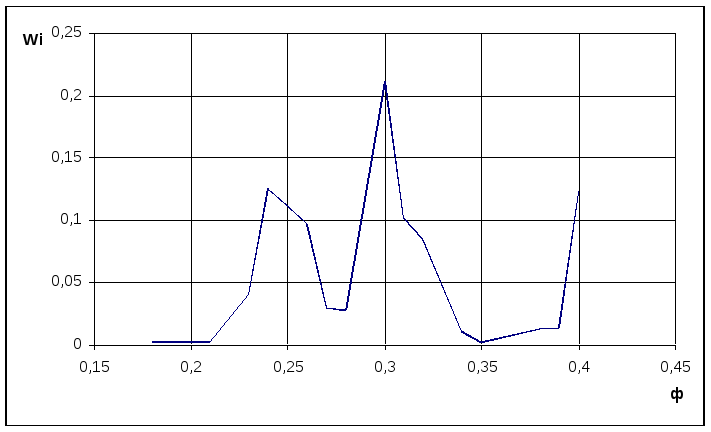
5. Определяем относительные частоты статистического распределения.

W_i =n_i/n

1	16872	0,4	0,12259	0,18	0,002405
2	1958	0,39	0,014227	0,2	0,00226
3	1771	0,38	0,012868	0,21	0,002005
				0,23	0,040747
5	272	0,35	0,001976	0,24	0,125372
6	1444	0,34	0,010492	0,25	0,111429
				0,26	0,096752
8	11751	0,32	0,085381	0,27	0,029899
9	14074	0,31	0,10226	0,28	0,027639
10	29136	0,3	0,211698	0,3	0,211698
				0,31	0,10226
12	3804	0,28	0,027639	0,32	0,085381
13	4115	0,27	0,029899	0,34	0,010492
14	13316	0,26	0,096752	0,35	0,001976
15	15336	0,25	0,111429	0,38	0,012868
16	17255	0,24	0,125372	0,39	0,014227
17	5608	0,23	0,040747	0,4	0,12259

и строим полигон частот

Лекция № 5. Прикладные вопросы статистической обработки результатов эксперимента.

Определение необходимого объема выборки¹³

При проектировании выборочного наблюдения возникает вопрос о необходимой численности выборки для получения достоверных данных. Эта численность может быть определена на базе допустимой ошибки при выборочном наблюдении исходя из вероятности, на основе которой можно гарантировать величину устанавливаемой ошибки, и наконец, на базе способа отбора.

Для определения необходимой численности выборки исследователь должен задать уровень точности выборочной совокупности с определенной вероятностью. В частности, необходимая численность случайной повторной выборки определяется по формуле

,

Эта формула показывает, что с увеличением предполагаемой ошибки выборки значительно уменьшается необходимый объем выборки. Так, увеличение допустимой ошибки выборки в 2 раза уменьшает необходимый ее объем в 4 раза. Необходимая численность выборки прямо пропорциональна дисперсии признака и величине t².

Одним из наиболее важных и в то же время сложных вопросов определения необходимого объема выборки в исследованиях является расчет показателя вариации изучаемого признака (σ). Во многих случаях точное представление об изучаемой совокупности в том числе о вариации интересующих исследователя признаков, может дать пробное обследование по его данным возможно рассчитать среднее квадратическое отклонение и дисперсию для последующего обоснования необходимого объема выборки. Если же мера колеблемости признака неизвестна, то ее можно найти приближенно по величине предполагаемого размаха или среднего линейного отклонения по следующим формулам:

или

где σ - среднее квадратическое отклонение;

R - размах вариации – разность между наибольшим и наименьшим значениями варьирующего признака;

- среднее линейное отклонение.

Важным условием практического использования этих формул является близость фактического распределения к нормальному. Исчисление среднего квадратического отклонения для явно не симметричных распределений не имеет смысла.

При статистическом исследовании СОциальноэкономич ЯВЛе очень часто Приходится сталкиваться с качественными ПризНаками, Причем именно по Ним нередко Проводится расчет необходимого Объема ВЫбОРОЧНой СОВОКУПНОСТИ Способ Выра-. жения качественных признаКов не Позволяет рассчитать по ним средние значения, поэтому оценка колеблемости ПроизвОдится, как правило, исходя из долей единиц, обладающих значениями этих Признаков, т. е. выборочных долей. Выборочная доля так же называется частостью.

Если расчет проводится по качественному альтернативному признаку и неизвестна его доля в генеральной совокупности (хотя бы приблизительно), рекомендуется принять ее равной 0,5, так как дисперсия доли достигает максимума: о 0,25 при ‚ч = 0,5.

Преимущество такого приема заключается в том, что он по зволяет определить численность выборочной совокупности, не располагая данными предыдущих обследований, и не проводить пробных обследований. Возможность экономии времени и ре сурсов часто оказывается решающим фактором при обращении к данному методу.

Если же качественный Признак, по которому определяется необходимая численность выборочной Совокупности, не являет ся альтернативным, то использовать формулу о = (1

нельзя.

В ряде случаев приближенная оценка колеблемости может быть осуществлена с помощью превращения изучаемого при знака в альтернативный. Например, все категории работников предприятия можно условно разделить в зависимости от При надлежности работающих к рабочим и служащим. Однако при этом следует учитывать, что такое деление неизбежно приведет к потере некоторой части информации. Ведь существуют от дельные категории работников (МОП, охрана и др.), которые выде.iiяются в самостоятельные группы. Поэтому применять описанный выше прием можно лишь при условии, что суще ствует уверенность в незначительной доле неучтенных единиц во всей совокупности.

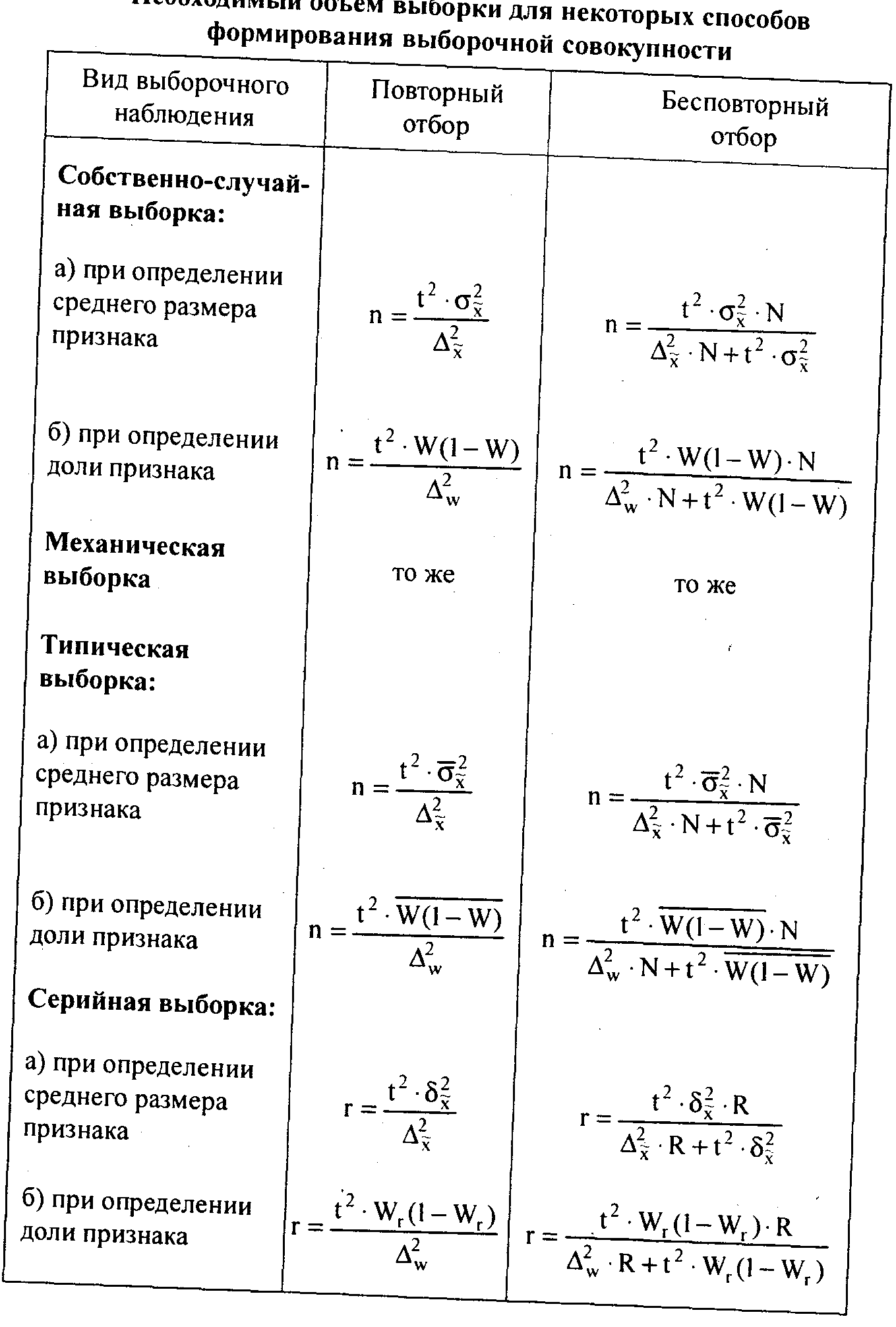
Приведем формулы необходимого объема выборки для наибо лее часто используемых -на практике способов формирования выборочной совокупности (табл. 8.6).

Рассмотрим несколько примеров расчета объема выборки при различных способах отбора.

Пример 1. В микрорайоне проживает 5000 семей. В порядке случайной бесповторной выборки предполагается определить средний размер семьи при условии, что ошибка выборочной средней не должна превышать 0,8 человека с вероятностью Р = 0,954 и при среднем квадратическом отклонении 3,0 челове ка (ошибка и среднее квадратическое отклонение определены на основе пробного обследования).