Дельта – образные последовательности
Обобщённую сингулярную функцию можно представить как предел последовательности регулярных функций.
Можно многими способами строить последовательности регулярных функционалов, сходящихся к - функции.
Для того, чтобы
соответствующие функции
имели
- образный
вид, нужно, чтобы выполнялись следующие
условия:
1) Каково бы ни было
M
> 0, при
,
величины
ограничены постоянной, не зависящей
от a,
b,
(зависят только от M).
2) при любых фиксированных a и b, отличных от нуля
Итак, другими словами, чтобы последовательности регулярных функционалов имели - образный вид, нужно, чтобы регулярные функции удовлетворяли условиям
(10)
(11)
Рассмотрим следующие примеры:
1
.
Ступенька
f(x,a)
1/2a
– из нормировки
х
1) -a a
Тогда:
проверяем:
(12)
2) Проверим главное свойство:
При
Пояснение:
(13)
Тогда,
В силу непрерывности последовательность регулярных функционалов f(x,a) сходится к дельта функции
2. Лоренцев импульс
(14)
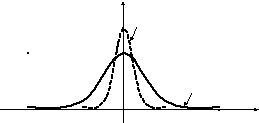y
x
Проверим свойства:
1)
(15)
2)
(16)
В силу непрерывности функционала
,
т.е.
3. Гауссов импульс
(17)
Центрированные нормальные кривые распределения
Покажем, что при
эта функция стремится к
- функции.
Заметим, что
,
поэтому, при любых a
и b
1
)
(18)
(Известно из нормального распределения)
Сделав замену
(эта замена переменных, чтобы отнормировать
кривую), мы видим, что
(19)
Далее, для гауссова
импульса для любого
(20)
(Пояснение:
безразмерная величина
,
интегрирование от b до , x – переменная интегрирования, поэтому правый интеграл больше левого).
Таким образом,
интегралы (20) по любому промежутку из
,
стремятся к нулю.
Аналогично, при
(-,
a),
a
< 0. Таким образом
есть дельтаобразная последовательность
и значит, что
(21)
4. Рассмотрим функцию
(22)
Покажем, что при
эта функция стремится к
- функции.
Известно, что по теореме Лобачевского:
Тогда, имеем для первого свойства
1)
(23)
Второе свойство:
2)
(24)
Отсюда следует,
что для всех
функции
образуют -образную
последовательность, т.е.,
что
;
(25)
1 В.С.Владимиров «Уравнения математической физики». - М.: Наука, 1971 г.
** И.М.Гельфанд, Г.Е.Шилов «Обобщенные функции». – М.: Физматлит, 1959 г.