Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский технический университет связи и информатики

Предмет:

Общая теория связи

Файл:

ТЭС

.pdf

Скачиваний:

Добавлен:

03.05.2015

Размер:

1.25 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 75 6 7 > Следующая >>>

- 42 -

r =	n k	= 1	k			(84)
	n		n

) k n					. Yn (		-
k ), (		, ' (
! .
6 k = 2						– r	= 1,
n = k + r = 3 #						N0 = 23 = 8 : 000;
001; 010; 011; 100; 101; 110; 111.
" (" #) # -
# , #					( ), -
( # )				"		. *

! ' # ! # ( ( . U-

, ! ! #

' – ! ( . % ( !

# ,			dmin	= 2 . 2
( ( ! . $				, (
!	t
dmin : t + 1					(85)
"[ "				-
", R		,			"
	R ,		, . .		,
! ! . 6 ! t					, -
(		'
dmin : 2t + 1					(86)

r ) -

d min ! ; ! , d min = 3			r : log(n + 1) ,
dmin = 4	r : log 2n .
5.5. L ' ' :			.
(
#(		); ( # -
. M ' ,
)	" # ( ). *-

-43 -

' (n, k) – , ) n – , k – " #-

. 1 ,

" # . % ' -

. 1 " , mod 2 '

# ( #. % -

, k ai # ' - " #, r = n – k Cj – , . . ' -

# ' ( x = (a1 ,a2 ,Kak ;c1 ,c2 Kcr ) .

5.6. % -

( ' #. ', R 0

G(n, k) ) (n, k) ' #,

# :

&1 0 0	K	0	C	C	K	C )


(			11	12		1r +
(			11	12		1r +
(0 1 0 K		0	C21	C22	K C2r +



G(n, k) = ( M		M	M			M +	,	(87)




(						+


'0 0 0 K		1	Ck1	Ck 2	K Ckr *

) – # k. 6 4j

' # " #

k		Aij =	0	i = j	(88)
Cj = 3aiAij ,		Aij =		i @ j	(88)
i=1			1	i @ j
, , (7,4) ( ' #
&	1000	011)



(		+


(	0100	101+
(	0100	101+
G(7,4) = (		+			(89)


	0010	110


(		+


' 0001		111*

1 ( # (89) k -

#. U (7,4) Nn = 2k = 16 #, $

12 # ( mod 2 ( '

5.7. !

# ! ) -

. , , , ! ) h ' ) -

. C ( ( '-

-44 -

#. 6 ( ' ' # (87)

G(n, k) = (1k Gr )

H ; = Gr; – ' # Gr ,) -

# H ! :

H(n,n k) = (H ; 1r )

*, , (7,4) # * (7,3)

&	0111	100)


H(7,3) = ((	1011	010++	(90)




(		+


'1101		001*

6 (a1, 2,… 7), ( (90) -

a2 ? a3 ? a4 ? a5 = 0 a1 ? a3 ? a4 ? a6 = 0 a! ? a2 ? a4 ? a7 = 0

& ( ( !

L . % –

mod 2 # -

, " " # (88). U ' ) )

! i i # #. 5.8. b ' , #-

$ # !

#. ' # '

v (x) =		x0 +	x1 +	x2 +K+	n 1	xn 1	; = 0; 1.	(91)
1	0	1	2		n 1

b ( (91) :

xv1 (x) = n 1 + 0 x + 1 x2 +K+ n 1 xn 2 = v2 .

a (n, k) " R g(x). & ) -

( ', ) xn ?1. 2 ( !

' # ( ' )

g(x): – ! ; ! " -

, ' ! . # )-

# .

-45 -

) ' " ". J

, - $ ' #. 2 '

, " '

( ' " # -

, ( ! '. &

" # , ' " ( ) ) -

) , ) ), -

). , "- # .

' ( " ", -

: , ,

!; , – . ,"" -

, ! , – .

6.! ' (

6.1. #

, ) '

( , - ,

. $ # ) ' '

" # , -

" , ' ! )

" # .

& ) (, ) )

# ". ) ) ' -

( *V), ' -

300…3400 Z#, ' " ) . # "-

' ' 64 / . C -

" " " " ' h *V )-, 12 . a " " (a4+) ( "- ' . 6

b% 51&–30 ' ) ) 2048

/ ; ( 51&–24 ' )-

- 46 -

) ) 1544 / . b%, ! , ' -

6.2. # ) '

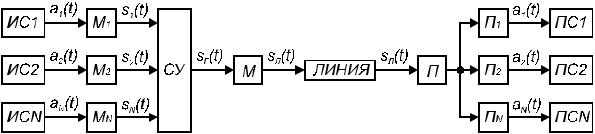
. 25. ) ' -

' N ) . %,

) ( ) ' ) i-) Si(t). - (, ) i-)

Si (t) = Ci4i (t) ,

(92)

) 4i (t) – " # ;

Ci – $"" #, ( ' . % ) ) )

N	N
S) (t) = 3Si (t) = 3Ci Bi (t) .		(93)
i =1	i=1

) ) ) ,

(' ). 9 S (t) ) ), . . , # ).

U N ) -

' N ' , ( )

k. k- ' (

) (“ ”) ) k-) Sk(t) -

) ) :

N	C			i = k	(94)
k = {Sr (t)} = k 3Ci Bi (t)	=		k	i @ k
i=1		0

9 ) (93)

" . 2 ' , (

L. 25

- 47 -

C1B1 (t) + C2 B2 (t)+K+Ci Bi (t)+KCN BN (t) C 0

(95)

( , ) $"" # C1, C2,… CN

' . J $ ,

) ( ) ). / -

		(B1B1 )	(B1B2 )	K (B1BN )

s(B1 , B2	,KBN ) =	(B2 B1 )	(B2 B2 )	K (B2 BN )	(96)
		M		M

		(BN B1 ) (BN B2 ) K (BN BN )

) (Bi Bk ) – . 2 (96) ', " #

B1, B2,…BN ( " #;

' " #, Bi Bk – ) . -

, ) ) -

( ' ) ) ) ) ' " # ' Bk(t)

N	T	N	T	(97)
k 3Ck Bk (t)	= Bk (t)3Ci Bt (t)dt = Ck Bk (t)Bk (t)dt = Ck			(97)
i=1	0	i=1	0

% # (97) ( ) )

# ) 1 . 5 ) (,

(97) ) " # Bi(t) Bk(t):
T	1	i = k	(98)
Bi (t)Bk (t)dt =		i @ k
0	0

% # ) (98) , Bi(t)

Bk(t), , " Si(t) Sk(t) R " "

6.3. $ " ) ) )

(VL1). M , ( ( -

ai(t) ) *V- ! . #

" ) ) ) ( ) Si(t) -

' ) ) ! i. * )

N- ) ! ) = 3! i . %, -

i=1

#, ( ) ! i =

-48 -

=! a = 6m , ) ) )

! ) = N! a = N6m .

Z ) S)(t) ) S (t), -

( ). 9 )

) ), ' " 5k -

! k ak(t), -

' '. / , " `=/ R " -

. 9 ) i-) ' ) Si

N . % ' " 5i ' !

D! i , ( i- . B -

" ' (

. U ( $ -

( ! z. , , VL1 $""

! 80% . 1 ), -

' ) ) ) .

6.4.(L1) ) -' (/ ) (/ ) -

) ( ) ) . %

) 1-) , ' ) . . ) -

N, ) ' 1- , # -

# f . W " W=/ - " " Si(t); -

– ) ) S)(t) . U / ( ( ', - ' ' i-) ( i-)

(“ " ” 5i). # ai(t) ' i-

( ( ( -. 7VW JVW , –

# ' .

L1 ( .

-49 -

L1 ) ( ) ' )

! ). 6 # T = 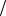6m , -

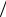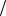!tk = T J = J6m = 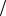! ) , . . ! ) = N6m . W -

L1 VL1 $ $"" ) -

, L1 ' VL1 $ -

' - ( ).

, L1 ( -

) (

, L1 ( -". % (, L1

VL1. 9 ! L1

# " 51&.

V )

(JL1). $ ) ' ) :

S1 (t) = a sin t , S2 (t) = a sin( t + !/) . !/ = 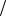2 ) S1(t) S2(t) ' - ) ) ' ' # -

. N > 2 Z ), ' ", -

. , , " ( ! -

' .

6.5.U ) ) ) -

' (VL1) ) ' -

(L1). ),

" , " ", -

. l ", -

(=/5). ! ) (

" , ( ' 1, t, t2,… ( 0 t T ). 9 - ) # " # ) ) T ), ,, V !, ) ) -

# " ) " ' - ) " # Y ! () “) ”

). 1 ( “ ” " -

. 2 # ) ) )

- 50 -

' # ,

2 ", ' -" " -(BB44). 77%% ( ) ) -

“ ) ” ). 1 ( ) !-

), " # # " # # )

! ) . 8 ) " '

. J -

“ ” . ( 77%% , -

# # #: “ ” -

) , . . “"” . U ) , )

) ' N ) N -

, N >> N . ) ' -

, ' “ ” , , , ( - ) 1000- ' , '-

50–100 .

6.6.# ) )

( # -

, ' #. *, ,

m = 2 ( 0 1) N = 2 ( #: 00, 01, 10, 11,

: 0, 1, 2, 3. 1 ( -

), , V& – f0, f1, f2, f3. 9

' ! " ( ' -

#, , , . * UV* ( ) "). 7- ) ( UJ* ( " ) "), $ )-

# ' ": /0, /1, /2, /3 ( . 26). U N-

M = 2N )

( , "). ( -

, , ", " . .

! ) - 0

(B5C), ) ' # ' " -

	- 51 -
L. 26	L. 27
'. 6 # ( '		-
) C(t) = ±1, ±3, $ 16-# 17J& ( .27). 9-

' ' )

) , ) ( ) .

6.7.' # " #. % # ' ) # " # ( )

" # ( ) h ' . +-

0 " -

" 0.

! " # (% L5) -

( . 28), ) (2) ) )

# “R " R "”. * ,

( N ( )

. ( 2 ) ! '

(N – 1) (, ' '-

2 ( ,

; (

'. , ) -

. 28 2 -

, , 2 N, -

N ( N 1)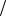2 .

L. 28

<<< < Предыдущая 1 2 3 45 / 75 6 7 > Следующая >>>

Соседние файлы в предмете Общая теория связи

#
03.05.20152.01 Mб49Теория цифровой связи. Ч.1.pdf
#
03.05.20152.25 Mб53Теория цифровой связи. Ч.2.pdf
#
10.07.2019969.22 Кб33тэс курс.doc
#
26.11.2019568.34 Кб17ТЭС на !.docx
#
19.07.2019524.24 Кб106тэс тестовые.docx
#
03.05.20151.25 Mб37ТЭС.pdf