
ТЭС
.pdf
- 32 -
) h12 , #. ' # -
h12 , ), . . h12 p , ! !-
) = !. ( ( ,
! ) T25 = 0 . 5 ), h12 > h12 p -
" " b/C .
, ( #.
% ! ( , ' ) -
, ( " )
. 6 ) ( ( ), $
' ! ! ". # -
U51& U& $"", “ ” !, ' " ) .
4.!
4.1.% '
'. *, , )
. & ) ( . ,
) " . 9 , ( ',
. 2 ". B
: ( #
( . * ( ": , , (- ' . 9, , -
, , , ( (, (
- -). 7 ( )
" ( – $ , -
" " #, (
. 2 h, $ -
. V ( ,
" #, ( .
( ) $"" -
. I R R -
0, " " 0 . I

-33 -
R 0, -
R R
" .
4.2.L " # -
.
$ {ai}, ( -
( . % $ -
A = {a1 ,a2 ,Kam } , ' ( ,
", $ m –
". – $ " ) ;
# " – ,
– ( ( . , ai !
" .
b 0, R ai , R
P(ai).
6 ' , ) -
ai, . . $) - #, ' " #. 6 $ -
#, , ai -
! -
(" #). V ! ai,
! ' " # ' ai. i R -
0, R ai,
Ii; = log |
1 |
= log P(ai ) |
(65) |
|
P(ai ) |
||||
|
|
|
) P(ai) – ai " # "-
A = {a1 ,a2 ,Kam } . 2 ) " # "-
#. , $ '
(m = 2) “0” “1”, P(ai ) = P(1) = P(0) = 21 ,
) ", 2,

- 34 -
1 |
|
|
|
Ii; = log2 P(ai ) |
= log2 2 = 1 |
# ( ) |
(66) |
0 0 ( Binary Digit – bit).
4.3. 4 0, R ( , 0) " R-
" I1; :
m |
|
|
||
H( A) = M[I1;] = 3 P(ai ) log2 P(ai ) |
|
(67) |
||
|
||||
i =1 |
|
|
||
6 P(ai ) = |
1 |
, |
|
|
m |
|
|
||
H( A) = log2 m |
|
(68) |
||
B ! " $ , '
P(ai), ) ), , ,
) . 2 P(a j 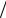 ai ) '
ai ) '
aj, ! ' ai. * ) " #,
ai $
m
Ii; = 3 P(a j ai ) log P(a j ai ) . (69)
j=1
% " # $ -
m |
m |
m |
|
H( A) = M[Ii;] = 3 P(ai )Ii; = 3 P(ai )3 P(a j ai ) log P(a j ai ) . |
(70) |
||
i=1 |
i=1 |
j=1 |
|
V (70) ' (67)
(68) . 9 #, ,
(70)
|
1 |
m |
m |
|
|
H( A) = |
33 P(a j ai ) log P(a j ai ) |
(71) |
|||
|
|||||
|
m i=1 |
j=1 |
|
||
l , " " "
H( A) = Hmax = log2 m |
|
|
W *(B) " 0 .
4.4. 6 ' ' <K . . ,
( ( " # *(B) / ., ) -
( )

- 35 -
RK = <K H( A) |
(72) |
% (68) 0
RK = <K
4.5. !, -
P(1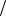 0) P(0
0) P(0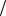 1) ( ) = = 0,5 , -
1) ( ) = = 0,5 , -
, . . R = 0.
9 . 9
bi ( [ log2 P(bj )] . ., $ 9( ).
, ai (
bi ' P(bj 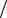 ai ) , $ $ (
ai ) , $ $ (
9( /7) ) (70). / 0
R *(W) *(W/B), . .
|
I (B, A) = H(B) H(B A) , |
|
|
I ( A, B) = H( A) H( A B) , |
|
0 |
|
|
|
RK = <K I (B, A) = <K [H(B) H(B A)] = <K [H( A) H( A B)] |
(73) |
4.6. C "
CA/4 = max RK ,
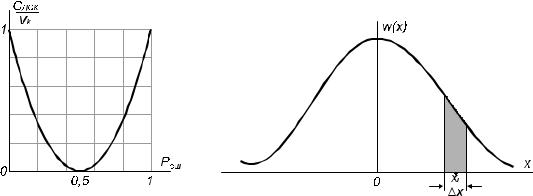
) ) ( P(0) = P(1) = 12 ; P(10) = P(01 ) = P )
(
CA4/ = <K [1 + P log2 P + (1 P ) log2 (1 P )] |
(74) |
Z " U%1 = . 21; -
“ ” –
(.
- 36 -
L. 21 |
L. 22 |
4.7. + (67) i " " -
x(t). , , x(t) ( c ( -
# !t) ' ! ) -
!x. * ) ) ± xmax
m = (2xmax 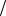 !x + 1) . 6, J " # x(t) ( .
!x + 1) . 6, J " # x(t) ( .
22), ( i-) ) |
|||||
|
|
, . . P( |
|
) 8 w(xi )!x . * ) (67) |
$ ) ) |
|
xi |
xi |
|||
: |
|
||||
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
||||
H(x) = 3 P(xi ) log P(xi ) = 3w(xi )!x log w(xi ) + 3w(xi )!x log !x |
||||||||||
|
|
i |
|
|
|
|
i |
i |
|
|
= 3w(xi ) log w(xi )!x log !x ,
i
3w(xi )!x = 1.
i
!x 0 , , $ )
|
|
|
|
|
|
|
H(x) = lim[H( |
|
)] = w(x) log w(x)dx + lim log |
1 |
(75) |
||
x |
||||||
!x |
||||||
!x 0 |
|
|
!x 0 |
|
||
) (75) 0 -
"
|
|
h(x) = w(x) log w(x)dx |
(76) |
(76) , ! ) ,

-37 -
J w(x). $ h(x) ( -
( , # . 76
! x(t). V ( ) ) ),
!x 0 . 2 ( ' -
, , ' -
' $ . $ ( (75) '
.
4.8.+ "
R 0 -
: FK, ! )–!
h12 = Pc 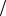 P . * (, , -
P . * (, , -
). & -
" #
, ) -
$ . U x(t) ' Pc
x2 w(x)dx = x2 = PC = const
max h(x) )
w(x) = |
|
1 |
|
e |
x2 |
|
|
|
2 2 |
||||
|
|
|
||||
2 |
||||||
|
|
|
|
|||
h(x) = log2 
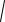 2 e x2 .
2 e x2 .
8 (t) # ) !,
) "" # $
h( ) = log2 
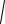 2 e 2
2 e 2
)
y(t) = x(t) + (t) ,
) "" # $
h( y) = log2 
 2 e y2 = log2
2 e y2 = log2 
 2 e( x2 + 2 .
2 e( x2 + 2 .
B $ ' ' "" # $ -
) (73),

- 38 -
I ( y, x) = h( y) h( y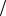 x)
x)
, , h( y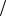 x) = h( ) ,
x) = h( ) ,
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
& |
PC |
) 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
I ( y, x) = log |
|
|
|
|
log |
|
|
|
|
|
= log |
|
1 + x |
= log |
|
(1 + |
|
|
|
||||||||||||
|
|
2 e( 2 |
+ 2 ) |
|
|
|
2 e 2 |
|
|
+ |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
P |
||||||||||||||||||||||||
|
2 |
|
|
x |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
2 |
' |
* |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
U ) |
( |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
& |
|
|
) |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
C*/4 = <K I ( y, x) = |
<K log(1 + |
|
PC |
+ |
|
|
; |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
' |
|
Pi * |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1 <K |
= 2FK , $ |
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
& |
|
|
|
PC |
) |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
C |
|
|
= 2F log(1 |
+ |
|
+ |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
*/4 |
K |
' |
|
|
|
Pi * |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
, i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
& |
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
C |
|
|
= F log(1 + |
|
PC |
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(77) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
*/4 |
K |
' |
|
Pi * |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Z " (77) ! h2 = P |
P |
|
|
. 23 |
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
C |
|
i |
|
|
|
|
|
|
|
|
|
|
|
||||
4.9.2 ( ' 4*/4
. 6 ( (77) Pi = G0 FK , PC = G0 F0 (G0 –
!; F0 – $ ),
|
C |
|
= |
F |
& |
+ |
|
G0 F0 |
) |
|||||
|
|
log(1 |
|
+ |
||||||||||
|
|
|
|
|
|
|||||||||
|
|
*/4 |
|
|
K |
' |
|
|
G0 FK * |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
C*/4 |
|
|
|
& |
|
|
|
) |
|
||||
|
= |
|
FK |
log(1 |
+ |
|
F0 |
+ |
(78) |
|||||
FK |
|
|
||||||||||||
|
|
|
F0 |
' |
|
|
|
|
FK * |
|
||||
Z " (78) . 24. p C*/4 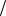 FK
FK
L. 23 |
L. 24 |
- 39 -
FK 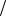 F0 F/, -
F0 F/, -
) ! # ( . 2.10.).
5.! "#
5.1.', " m- "-
r = |
Hmax ( A) H( A) |
= 1 |
H( A) |
(79) |
Hmax ( A) |
log m |
2 " # " -
: r = 0, " ', r > 0, , #
, ( . 9 -
) , ( r ' ' , -
.
5 ' . L # " # '
.
%, ! " #-
, ! $) .
%) , , ' " # -
', ' ' , $ , ' ,
-
# .
5 $ " # )
' : ' # ' ! ' ( -
') , $"" , - ) , ' (')
! ( ) .
q " –
" " ( – ),
" , " " ( – -
). q " -
, " ".
-40 -
5.2.( $ ( -
) ) # . ai " B ' A = {a1 ,a2 ,Kai ,Kam } ,
" m ' " . *, , ) " m = 32, . . (
0, 1, … 31. B ( -
# . 6 ) m -
( ), ' N ( n
#, )
n 1 |
|
N = 3= i mki |
(80) |
i=0 |
|
) =i – # , ' ' 0 < = i |
< mK 1 , - |
(m = 2) $"" # =i ) |
0 1. A - |
m n = log2 ma |
0. Y- |
# # , . . |
|
(= n 1 ,K= 0 ) > = n 1 2n 1 +K+= 0 20 , |
(81) |
) ' # ' ' ) ( -
' n = log2 32 = 5 . 9, v = 13 :
v= 13 > (01101) > 0 2 24 + 12 23 + 12 22 + 0 2 21 + 12 20 .
-
# ( " . 6
# ' ( n, ' , n – .
5.3.W R -
, . . R ,
- . 5 ( ( ! ( . . -
# " #) . 2 ,
( ) ' N0 = mkn -
( #, ! N < N0 . 5
N # ' ! (" #-
), ( N0 N ) # – . q
- 41 -
( 0) -
", " R .
, , N = 4 (
( A, B, C, D). m = 2 n = 2 ( " # #: 00, 01, 10, 11. $ N0 '
" #, . . N0 = N .
2! ei ! ) ( ,
" # # (0 – ! , 1 – ! !). -
# ( ' 2 (mod 2) #
! ( mod 2 : 0 ? 0 = 0 , 0 ? 1 , 0 ? 1 = 1 , 1? 1 = 0 ). 1-
# .
( !.
%# ' # ' -
“ “ ( # (“ ”) W-
)
r r |
n |
|
||
|
xi yi |
|
(82) |
|
d(x, y) = 3 |
|
|||
|
i=1 |
|
|
|
1 ' min d(x, y) = dmin . U A , |
B , C D |
|||
dmin = 1, ,
' . B # N0 ' -
! " # # N0 = N .
5.4.L , ) N0 > N . N = 4, -
. n #
|
|
n = k + r |
(83) |
) k – " # , |
|
||
r – (') . |
|
||
* ) N0 |
= 2n |
– #, |
|
N |
= 2k |
– " # #, |
|
N p = 2n 2k – #.
5 ), r " $
'
