ТЭС
.pdf
- 22 -
" |
|
x(t) = S(t,a(t)) + (t) = a(t) f (t) + (t) |
(46) |
a(t) – (45). B S(t,a(t)) – ), f(t) – , (t) –
) !.
" #,
|
|
|
|
|
|
|
|
|
$ |
|
|
||
, ! (t) = S(t) S(t) |
|||||||||||||
) x(t), ( |
!, - |
||||||||||||
' : |
|
|
|
|
|
|
|
|
|
|
|
||
|
da |
|
= |
$ |
2k |
|
$ |
(t) f (t)], |
(47) |
||||
|
dt |
G0 |
|
||||||||||
|
a(t) + |
|
f (t)[x(t) a |
||||||||||
|
dk |
|
= |
|
N1 |
2 k |
|
|
2 |
f 2 k 2 |
|
(48) |
|
|
dt |
2 |
|
|
|
|
|||||||
|
|
|
|
|
N0 |
|
|
||||||
[ (47) (48) " /. Y-
(47) ) " #, , '
" , (48) – ! " # 
. % , -
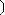' (47) . 14. , " -
' $"" # , )
# ( ) ! " # ) ! - '. 5 ), " 1 ( ' - ' , $"" , # -.
2.7. L 0
" " . |
a(t), |
||||||||
|
|
a(t) |
|
1, ) |
|
; a(t) ( - |
|||
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L. 14
- 23 -
n
( a(t) = 31i4i (t) ) '
$"" # 1i. * ) ) S(t;a) = S(t;11 ,12 ,K1n ) #
dS(t)
# # Di = d1i , -
' .
% ) , ) S (t) '
(t) ) S(t). 1 $), $"" #
1i = 1i + !1i ( 1i.
a (t) = 31i 4i (t) = 3(1i + !1i )4i (t) = (49) = a(t) + 3!1i 4i (t)
) !
(t) = a (t) a(t) = 3!1i 4i (t)
2.8. 2 1
R = [S (t) S(t)]2 .
& ' R ' !1 , |
||||
|
|
|
|
i |
|
dR |
|
dS |
|
|
d1i |
= 2[S |
(t) S(t)] d1i |
= 0 , |
. . |
!1i = (t)Di (t) . |
(50) |
||
|
|
D2 |
(t) |
|
|
|
i |
|
|
9 (50) ( !
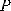
. 1 ), (t) ( ,
' ! (
G |
( ) = |
G ( ) |
, |
(51) |
||
D2 |
(t) |
|||||
|
|
|||||
|
|
i |
|
|
|
|
P |
|
|
|
|
|
|
|
b |
|
|
|
|
|
P |
= G ( )d . |
(52) |
||||
|
0 |
|
|
|
|
|
|
|
|
|
- 24 - |
% - |
|
|||
" - |
|
|||
|
|
|
|
|
h2 |
= Pa = |
1 |
. |
(53) |
2 |
P |
|
|
|
|
b G( )d |
|
|
|
|
|
0 |
|
|
2.9. ( (52) (53) - |
|
|||
' 0 - |
|
|||
0 - |
|
|||
" 0. - |
L. 15 |
|||
|
|
|
|
|
' ( |
|
|||
G ( ) h22 :
7& |
S(t) = A[1 + ma(t)]cos 0t |
|
|
|
|
|
|
|
|
|
|
||||||||
|
G ( ) = |
2G |
0 |
|
, |
|
|
|
h2 |
= |
|
m2 A2 |
|
(54) |
|||||
|
m2 A2 |
|
|
|
|
2G0 b |
|||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
||||||||
J& |
|
[ |
|
0 |
t + !/ |
m |
a(t) |
] |
|
|
|
|
|
|
|
|
|
||
S(t) = Acos |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
G ( ) = |
2G |
0 |
|
|
|
|
|
|
= |
!/ 2 |
A2 |
|
|
|||||
|
|
|
|
, |
|
h2 |
|
|
m |
|
|
|
(55) |
||||||
|
!/m2 A2 |
|
|
2G0 b |
|||||||||||||||
|
|
|
|
|
|
2 |
|
|
! m |
||||||||||
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|||
V& |
S(t) = Acos 0t + ! m a(t)dt ; a(t) = cos6t ; 5 = |
|
|
||||||||||||||||
7 |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
G ( ) = |
2G |
0 |
|
|
|
|
|
|
= |
|
|
5 2 |
A2 |
|
|
|||
|
|
|
|
|
, |
|
h2 |
3 |
|
|
|
|
(56) |
||||||
|
! m2 A2 |
|
|
2G0 b |
|||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
||||||||
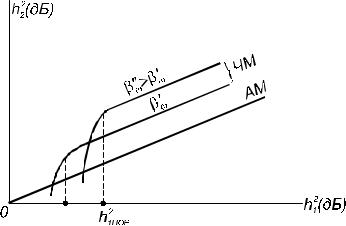
Z " G ( ) 7&, J& V& (54), (55) (56) -
. 15.
5 (54 – 56) , 7& (m = 1) R
; 5C `C R-
R 0 !/m 5 , -
.
-25 -
2.10.! # ' ' -
h22 , ! )– h12 ! -
) ) ) ( . 16). h12 < h12 p ! '
( ( ); ' $ -
' . & ( ) )
) ) # ( , V&) )
) -
, ) ) !
! = 2(5 + 1)6b . '
" Y V ! a 8 26b , ! a – ! )-
) , ( $) )
( . 10). $ ! ( 5 ,
( ( ' ) ) h12 p .
3.! ! ! "#
3.1.2 )-
' ()) ) -
. ,
" (#) ). *-
) – , - -
! (. ) ' # ,
L. 16 |
- 26 -
( ) ), ' ( '
. % # ' $"" #
# " ' ) # ' ) ' - # ' .
U # " -
# " ' ", . . ) ) #
#, . , # ' - 0 (Ba+) ' ; -
0 0- (aB+). 2 )-
7b ' #
– - 0 (b/C). b7
' , - # ' , ) ( ' " , -
' .
3.2.# " ' "
51& ( ) ) ai ( ! !-
ai . ' $ ) !
(t) = ai ai . Y ! ! ) !a (
) ) ! . 2 $ -m – ( ) , -
n = log2 ma ). ' ,
! ) 51&. 9,
N = a20 + b21 + c22 + d23 +K, )$"" # a, b, c, d,… ) 0 1. $ -
! 1, 3, 5, )
001, 011, 101 ( . 17).
- 27 -
L. 17
! ) ! -
! !a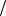
2 . 6 ) -
a(t) 2amax , ma = (2amax 
!a) + 1. m >>1
( , ! ' |
- |
||||||||
± !a 2 . * ) ! |
|
||||||||
|
|
|
|
!a |
|
|
|
|
|
|
|
= |
1 |
|
2 |
2d = |
!a2 . |
|
|
2 |
|
(57) |
|||||||
|
!a |
|
|||||||
|
|
|
|
!a |
12 |
|
|||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 a(t) ( ' J ± amax,
)
|
|
1 |
amax |
a2 |
|
!a2 (m |
1) |
|
|
a2 = |
a2 da = |
= |
|
|
|||||
|
max |
a |
|
. |
(58) |
||||
|
|
|
|||||||
|
|
2amax amax |
12 |
|
12 |
|
|
|
|
* , ! !
|
|
|
|
|
|
|
h2 |
= a2 |
|
= (m 1)2 |
(59) |
||
|
||||||
|
|
|
2 |
a |
|
|
|
|
|
|
|
|
|
W" ma , R
".
! (
! , , ! -
-28 -
' ! ! ), – ! ! ). -
$ , '
- -
: ( “(” ) ), '
$ ( ) ).
3.3.51&- ) !
51&-) ' ) . 9 -
' ! 51&-) mk = 2 . 6 !-
) F , #
1 2F . 1 (
( ma = (2amax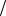 
!a) + 1 ( ai -
# n = log2 m . % ,
( ) ( !, 1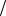
(2Fa log2 ma ) , -
F = 1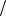
(2 ) = Fa log2 ma . , ,
" b/C R b/C ) " . U ) , 51&, -
) # “ ” )-
.
3.4.( , , , -
(, ( ' , -
, # . 9 $""-
" #.
L –
( . 18). ai )
) ' ) (Y), ) – -
a~i = f (ai 1 , ai 2 , ai 2 ,K) , " " -
(J) . L ) '.
L. 18
- 29 -
) i ( , -
' ( ,
. % ,
. 9 # ( , '. -
( ,
a~i (, . U -
) ) i , (
ai = a~i + i .
2, # , ( "-
) , , ! $) -
) ) ' ). - # a~i ( :
|
~ |
= f [ai 1 ]. |
|
ai |
|
2 ) ! ' ) ' |
||
|
~ |
= ai 1 , |
|
ai |
|
|
i |
= ai ai 1 . |
|
U , $) ) ) |
|
|
|
(60) |
) |
– $"" # # ( . |
|
5 (60) , b > 0,5 E -
E .
3.5.# " ) ) ) '
# . L )
' 51& – ) ), "-
Ab/C (0 " b/C). !
# . 2
' # " ) ):
) " ) ", ,
) – ) ), " -
). L ! # ! .
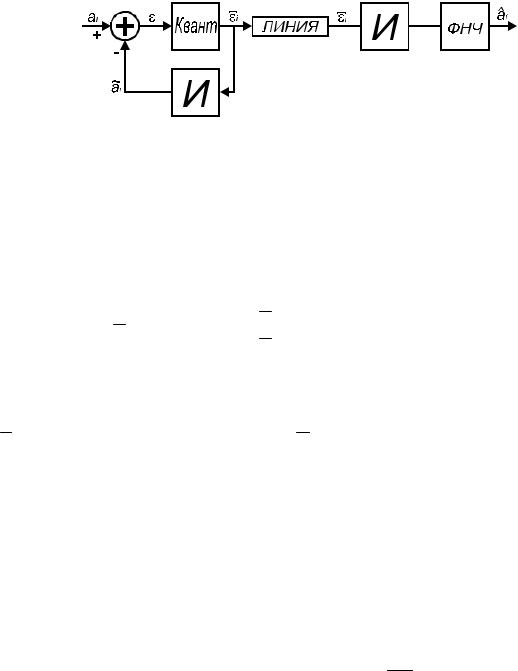
- 30 -
L. 19
3.6. 1 # ( - ( . $ ! #
) ) ( ' m = 2. * -
' -# (U&). 1 )
$
= + !a , ai : ai
i!a , ai < ai
+ " AC R . U
) )
i . " # ai ( ) ( ' J9V.
% U& . 19.
# U& 51& , AC -
( ),
$ # ( !
!t |
1 |
|
|
|
a(t) |
|
max |
. |
(61) |
|
|
|
|
|
|
||||
m |
|
a;(t) |
|
|
|||||
|
|
||||||||
|
|
|
max |
|
|||||
|
|
|
|
|
|
|
|
||
' (, “
”, , " # a(t)
a(t) ( . 20). ' 51& ) U&
' ' #. , -
, U& , 51& ( -
) ,
51& U& . $ ' -
' . % -
U& ' ' . 2, ) ! ' ) -
- 31 -
) ) |
) ) |
L. 20 |
|
U51& U&, , ! !-
' ! )
) .
3.7.' R " -
b/C. 2 ! ) ) -
# = . , #
" 2. ) ! , - ! ( P (q) – ), ! -
q:
P |
(q) = Cq Pq |
(1 P )n q . |
(62) |
|
n |
|
|
), # !
nP << 1,
[1 (1 P )n ] . nP . |
(63) |
( #, - ) , “ ” . 6
, ! ! # ) !-
, ' ! ) ! ; !
) ! 2! . . $ !, )
( ,
|
|
= [1 (1 P )n ] |
!a |
2 |
n |
n |
|
|
T52 |
|
322(i 1) |
8 322(i 1) |
(64) |
||
|
n |
|
|||||
|
|
|
|
i=1 |
i =1 |
|
" n = log m ! ( -
! = , , ' , !