
- •1 Вопрос Определители 2-го порядка
- •2 Вопрос Миноры и дополнения
- •3 Вопрос Определитель n-го порядка
- •3.1 Метод математической индукции
- •3.2 Вычисление определителя n-го порядка по минорам и ад
- •3.3 Верхне треугольный определитель
- •4 Вопрос
- •5. Вопрос
- •6 Вопрос. Системы линейных уравнений Определенность системы линейных уравнений. Совместность, несовместность (6.1)
- •Матричная форма записи m линейных уравнений с n неизвестными
- •9 Вопрос
- •Эквивалентные матрицы и системы
- •Ступенчатые матрицы; сведение матрицы к ступенчатой
- •10 Вопрос (Метод Гаусса) Решение произвольной системы линейных уравнений
- •11 Вопрос
- •12 Вопрос
- •14 Вопрос
- •Сложение векторов
- •Свойства линейного пространства
- •2) Ассоциативность
- •15 Вопрос а) Линейно – зависимые векторы и их свойства
- •Б) Формулировки теорем о линейной зависимости коллениарных и компланарных векторов
- •В) Формулировка теоремы о линейной зависимости четырех векторов.
- •16 Вопрос
- •19 Вопрос Исследование систем линейных уравнений Однородные системы
- •Решение неоднородных систем
- •Доказательство достаточности теоремы Кронеккер-Капелли
- •Доказательство критерия определённости системы
- •20 Вопрос
- •21 Вопрос
- •Свойства векторного произведения .(антикоммутативность, линейность и однородность)
- •Доказательство Леммы 25.1:
- •Векторное произведение базисных ортов
- •Свойства смешанного произведения
- •28 Вопрос Смешанное произведение векторов в координатной форме
- •36 Вопрос
- •Общее уравнение плоскости и его исследование
- •37 Вопрос Условия параллельности и перпендикулярности двух плоскостей, угол между ними Взаимное расположение двух плоскостей
- •Условие перпендикулярности
- •38 Вопрос
- •Уравнение плоскости, проходящей через три заданные точки
- •Уравнение плоскости в отрезках
- •39 Вопрос Расстояние от точки до плоскости
- •40 Вопрос Прямая как пересечение двух плоскостей. Общее уравнение прямой в пространстве
- •Каноническое уравнение прямой как уравнение прямой в пространстве проходящей через заданную точку и коллинеарной заданному вектору
- •Параметрическое уравнение прямой в пространстве
- •41 Вопрос Приведение общего уравнения прямой к каноническому виду
- •2) Найти направляющий вектор прямой .
- •Условие ортогональности и перпендикулярности прямых
- •44 Вопрос
- •Угол между прямой и плоскостью. Условие их перпендикулярности
- •Точка пересечения прямой и плоскости
- •45 Вопрос Расстояние от точки до прямой в пространстве
- •46 Вопрос Расстояние между скрещивающимися прямым
- •47 Вопрос
- •(47.17)
- •(47.31)
- •(47.18)
- •(47.20)
- •(47.24)
- •(47.25)
- •Эллиптический цилиндр
- •II. Гиперболический цилиндр
- •III. Параболический цилиндр
- •(47.32)
- •(35.21)
- •(47.36)
Б) Формулировки теорем о линейной зависимости коллениарных и компланарных векторов
Теорема 16.0:
 –
л.з.
–
л.з.
 (если
(если
 ,
, то
вектор
то
вектор ).
).
Теорема 16.1: 2 вектора линейно зависимы, тогда и только тогда, когда они коллинеарные.
Доказательство:
 (Смотри
п14.2(§14) правило 1) определение)
(Смотри
п14.2(§14) правило 1) определение)
Если
 ,
то
,
то
 ( “+”, если
сонаправленны; “–“, если противоположно
направлены).
( “+”, если
сонаправленны; “–“, если противоположно
направлены).
(читателю предлагаем
самостоятельно доказать, что если
 («+»,
если
(«+»,
если и
«-» то
и
«-» то ),
то
),
то и
и )
т.е
)
т.е )
)
Причём, если
 ,
то
,
то ,
и
,
и и, таким образом, свойство (5) суммы и
умножения векторов на число (см.31.4)
полностью доказано.
и, таким образом, свойство (5) суммы и
умножения векторов на число (см.31.4)
полностью доказано.
Теорема 16.2: 3 вектора линейно зависимы, тогда и только тогда, когда они компланарные.
Доказательство:
 –л.з.
–л.з.
 и они компланарны, ибо
и они компланарны, ибо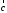 является диагональю параллелограмма,
на сторонах которого лежат векторы
является диагональю параллелограмма,
на сторонах которого лежат векторы и
и .(см.
рис 16.1)
.(см.
рис 16.1)


В

Пусть
 – компланарны;а
– компланарны;а (иначе
(иначе

содержит линейно
зависимую подсистему



 ;
;
 ,
, .
.
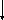

Тогда
 O
O

 A
A
Рис 16.1
Мы показали так же что справедлива
Лемма 16.1: если
 неколлинеарные,
неколлинеарные,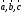 компланарные, то
компланарные, то ,
что
,
что .
.
В) Формулировка теоремы о линейной зависимости четырех векторов.
Теорема 16.3: 4 вектора всегда линейно зависимы.
Доказательство:
Пусть
 выходят из общего начала (точки О). Можно
считать, что среди векторов
выходят из общего начала (точки О). Можно
считать, что среди векторов нет компланарных троек (иначе существует
л.з. подсистема). Из конца вектора
нет компланарных троек (иначе существует
л.з. подсистема). Из конца вектора (т.D)
проводим прямую до её пересечения с
плоскостью, на которой расположены
векторы
(т.D)
проводим прямую до её пересечения с
плоскостью, на которой расположены
векторы
 и
и .
Пусть М – искомая точка пересечения.
(см. рис 16.2)
.
Пусть М – искомая точка пересечения.
(см. рис 16.2)
Тогда
 и, следовательно,
и, следовательно, (16.1)
(16.1)
По правилу
треугольника,
 (16.2)
(16.2)
Векторы
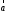 и
и не
коллинеарные, и тогда
не
коллинеарные, и тогда (16.3)
(16.3)
Подставляя вместо
 в
(16.2) его выражение по формуле (16.3), получаем
в
(16.2) его выражение по формуле (16.3), получаем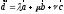 ,
т.е.
,
т.е. линейно
выражается через векторы
линейно
выражается через векторы ,
и система
,
и система – л.з.
– л.з.






D
C B M
O A
16 Вопрос
Линейная зависимость колениарных и компланарных векторов. Линейная зависимость четырех векторов.
Формулировки теорем о линейной зависимости коллениарных и компланарных векторов
Теорема 16.0:
 –
л.з.
–
л.з.
 (если
(если
 ,
, то
вектор
то
вектор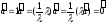 ).
).
Теорема 16.1: 2 вектора линейно зависимы, тогда и только тогда, когда они коллинеарные.
Теорема 16.2: 3 вектора линейно зависимы, тогда и только тогда, когда они компланарные.
Формулировка теоремы о линейной зависимости четырех векторов.
Теорема 16.3: 4 вектора всегда линейно зависимы.
Доказательство теорем
Доказательство теоремы 16.1:
 (Смотри
п14.2(§14) правило 1) определение)
(Смотри
п14.2(§14) правило 1) определение)
Если
 ,
то
,
то
 ( “+”, если
сонаправленны; “–“, если противоположно
направлены).
( “+”, если
сонаправленны; “–“, если противоположно
направлены).
(читателю предлагаем
самостоятельно доказать, что если
 («+»,
если
(«+»,
если и
«-» то
и
«-» то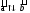 ),
то
),
то и
и )
т.е
)
т.е )
)
Причём, если
 ,
то
,
то ,
и
,
и и, таким образом, свойство (5) суммы и
умножения векторов на число (см.31.4)
полностью доказано.
и, таким образом, свойство (5) суммы и
умножения векторов на число (см.31.4)
полностью доказано.
Доказательство теоремы 16.2:
 –л.з.
–л.з.
 и они компланарны, ибо
и они компланарны, ибо является диагональю параллелограмма,
на сторонах которого лежат векторы
является диагональю параллелограмма,
на сторонах которого лежат векторы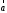 и
и .(см.
рис 16.1)
.(см.
рис 16.1)


В

Пусть
 – компланарны;а
– компланарны;а (иначе
(иначе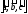

содержит линейно
зависимую подсистему
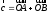


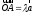 ;
;
 ,
, .
.


Тогда
 O
O

 A
A
Рис 16.1
Мы показали так же что справедлива
Лемма 16.1: если
 неколлинеарные,
неколлинеарные, компланарные, то
компланарные, то ,
что
,
что .
.
Доказательство теоремы 16.3:
Пусть
 выходят из общего начала (точки О). Можно
считать, что среди векторов
выходят из общего начала (точки О). Можно
считать, что среди векторов нет компланарных троек (иначе существует
л.з. подсистема). Из конца вектора
нет компланарных троек (иначе существует
л.з. подсистема). Из конца вектора (т.D)
проводим прямую до её пересечения с
плоскостью, на которой расположены
векторы
(т.D)
проводим прямую до её пересечения с
плоскостью, на которой расположены
векторы
 и
и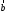 .
Пусть М – искомая точка пересечения.
(см. рис 16.2)
.
Пусть М – искомая точка пересечения.
(см. рис 16.2)
Тогда
 и, следовательно,
и, следовательно, (16.1)
(16.1)
По правилу
треугольника,
 (16.2)
(16.2)
Векторы
 и
и не
коллинеарные, и тогда
не
коллинеарные, и тогда (16.3)
(16.3)
Подставляя вместо
 в
(16.2) его выражение по формуле (16.3), получаем
в
(16.2) его выражение по формуле (16.3), получаем ,
т.е.
,
т.е. линейно
выражается через векторы
линейно
выражается через векторы ,
и система
,
и система – л.з.
– л.з.






D
C B M
O A
