
- •1 Вопрос Определители 2-го порядка
- •2 Вопрос Миноры и дополнения
- •3 Вопрос Определитель n-го порядка
- •3.1 Метод математической индукции
- •3.2 Вычисление определителя n-го порядка по минорам и ад
- •3.3 Верхне треугольный определитель
- •4 Вопрос
- •5. Вопрос
- •6 Вопрос. Системы линейных уравнений Определенность системы линейных уравнений. Совместность, несовместность (6.1)
- •Матричная форма записи m линейных уравнений с n неизвестными
- •9 Вопрос
- •Эквивалентные матрицы и системы
- •Ступенчатые матрицы; сведение матрицы к ступенчатой
- •10 Вопрос (Метод Гаусса) Решение произвольной системы линейных уравнений
- •11 Вопрос
- •12 Вопрос
- •14 Вопрос
- •Сложение векторов
- •Свойства линейного пространства
- •2) Ассоциативность
- •15 Вопрос а) Линейно – зависимые векторы и их свойства
- •Б) Формулировки теорем о линейной зависимости коллениарных и компланарных векторов
- •В) Формулировка теоремы о линейной зависимости четырех векторов.
- •16 Вопрос
- •19 Вопрос Исследование систем линейных уравнений Однородные системы
- •Решение неоднородных систем
- •Доказательство достаточности теоремы Кронеккер-Капелли
- •Доказательство критерия определённости системы
- •20 Вопрос
- •21 Вопрос
- •Свойства векторного произведения .(антикоммутативность, линейность и однородность)
- •Доказательство Леммы 25.1:
- •Векторное произведение базисных ортов
- •Свойства смешанного произведения
- •28 Вопрос Смешанное произведение векторов в координатной форме
- •36 Вопрос
- •Общее уравнение плоскости и его исследование
- •37 Вопрос Условия параллельности и перпендикулярности двух плоскостей, угол между ними Взаимное расположение двух плоскостей
- •Условие перпендикулярности
- •38 Вопрос
- •Уравнение плоскости, проходящей через три заданные точки
- •Уравнение плоскости в отрезках
- •39 Вопрос Расстояние от точки до плоскости
- •40 Вопрос Прямая как пересечение двух плоскостей. Общее уравнение прямой в пространстве
- •Каноническое уравнение прямой как уравнение прямой в пространстве проходящей через заданную точку и коллинеарной заданному вектору
- •Параметрическое уравнение прямой в пространстве
- •41 Вопрос Приведение общего уравнения прямой к каноническому виду
- •2) Найти направляющий вектор прямой .
- •Условие ортогональности и перпендикулярности прямых
- •44 Вопрос
- •Угол между прямой и плоскостью. Условие их перпендикулярности
- •Точка пересечения прямой и плоскости
- •45 Вопрос Расстояние от точки до прямой в пространстве
- •46 Вопрос Расстояние между скрещивающимися прямым
- •47 Вопрос
- •(47.17)
- •(47.31)
- •(47.18)
- •(47.20)
- •(47.24)
- •(47.25)
- •Эллиптический цилиндр
- •II. Гиперболический цилиндр
- •III. Параболический цилиндр
- •(47.32)
- •(35.21)
- •(47.36)
Сложение векторов
Правило параллелограмма.
A C
 =
= +
+



(Векторы
а и b
не коллинеарные.)



O
 B
B
2) Правило треугольника
С
 =
= +
+



(Векторы
а и b
могут быть коллинеарные.)


О
 В
В
Умножение вектора на число
Правила(Определения):
1)
 ;
;
2)
 =
|λ| |
=
|λ| |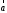 |;
|;
3)Эти векторы сонаправленны, если λ > 0, и противоположно направлены, если λ < 0.
Свойства:
0
 =
=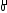 ;
;|
 +
+ |
≤ |
|
≤ | |
+ |
|
+ | |
и |
|
и | +
+ | = |
| = | |
+ |
|
+ | |
↔
|
↔ ↑↑
↑↑ –
–
 и
и параллельны и сонаправленны;
параллельны и сонаправленны;|
 -
- |
≥ ||
|
≥ || |
-|
|
-| ||
и |
||
и | +
+ | =| |
| =| | |
- |
|
- | ||
↔
||
↔ ↑↓
↑↓ –
– и
и параллельны и противоположно
направлены.При этом вектор
параллельны и противоположно
направлены.При этом вектор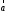 +
+ направлен
в сторону того из векторов
направлен
в сторону того из векторов
 или
или
 ,
который
имеет большую длину
,
который
имеет большую длину
Свойства линейного пространства
 +
+
 =
= +
+ (очевидно,
если сложить по правилу параллелограмма)
(очевидно,
если сложить по правилу параллелограмма)(
 +
+ )
+
)
+ =
= + (
+ ( +
+ )
) +
+ =
=
 + (-
+ (- )
=
)
=
λ(
 +
+ )
=λ
)
=λ + λ
+ λ
(λ + μ)
 = λ
= λ + μ
+ μ
(λμ)
 =
λ(μ
=
λ(μ )
)1×
 =
=
Докажем свойства 2) ÷ 8):
2) Ассоциативность
С
 +
+
 =
=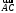


 +
+
 =
=


 + (
+ ( +
+ )
=
)
= +
+ =
= (14.1)
(14.1)
( +
+ )
+
)
+ =
= +
+ =
= (14.2)
В
(14.2)
В


(14.1) = (14.2)


О  А
А
Рис 14.3
3)
 +
+ =
=
По определению:
 –
–
 =
= + (-
+ (- ).
).
 =
=
 ,
тогда
-
,
тогда
- =
= :
:
 –
–
 =
= + (-
+ (- )
=
)
= +
+ =
= =
=
Пусть

 0 ,
0 ,
 0, λ
0, λ 0
(иначе 5-е свойство становится тривиальным:
0
(иначе 5-е свойство становится тривиальным: =
= ,
или ( при
,
или ( при = 0); λ
= 0); λ =
=
 λ), предположим:
λ), предположим:
 и
и неколлинеарные.(случай
неколлинеарные.(случай ||
||
 будет доказан
в §16 п.16.2)
будет доказан
в §16 п.16.2)
Пусть точка О –
начальная точка вектора .(см.
рисунок 14.4)
.(см.
рисунок 14.4)
В’


В
 =
=

 =
=
 λ
λ =
=
 λ
λ =
=


Также:
 ||
||
 (т.к. λ
(т.к. λ ||
||
 )
и
)
и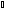 OAB
=
OAB
=
 OA`B`.
OA`B`.
Также:
 О
А А’
О
А А’
Рис 14.4
Поэтому ΔOA`B`
~ ΔOAB,
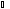 B`OA`
=
B`OA`
=
 BOA
, т.е точка B
лежит на прямой OB’.
BOA
, т.е точка B
лежит на прямой OB’.
Но
 `
=
`
=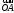 `
+
`
+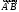 =λ
=λ
 +λ
+λ
 (14.3);
(14.3);
 =
=
 +
+ =
=
 +
+ (14.4)
(14.4)
 `||
`||
 ,
т.к. ∆OAB
~ ∆OA’B’
,
т.к. ∆OAB
~ ∆OA’B’
 ,
, т.е.
(14.5)
т.е.
(14.5)
Подставляем (14.3) и
(14.4) в (14.5) получаем λ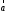 +
λ
+
λ = λ(
= λ( +
+ ).
).
Можно полагать, что λ
 0,
μ
0,
μ 0,
0,
 0,
иначе свойство (6) становится тривиальным:
0,
иначе свойство (6) становится тривиальным:
 =
=
 .
.
(или при μ = 0, λ = λ
= λ )по
определению (см.14.2 , правило 1)считаем,
что λ
)по
определению (см.14.2 , правило 1)считаем,
что λ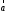 ║
║
 ,
μ
,
μ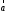 ║
║
 → (λa
+ μ
→ (λa
+ μ )
║
)
║
 (14.7)
(14.7)
и (λ + μ)
 ||
||
 (14.8).
(14.8).
Из (14.7) и (14.8) следует,
что (λ+ μ)
 || λ
|| λ + μ
+ μ .
.
Далее надо рассматривать следующие случаи:
а) λ > 0 , μ > 0
б) λ > 0 , μ < 0 , λ + μ > 0
в) λ > 0 , μ < 0 , λ + μ < 0
г) λ < 0 , μ < 0
Рассмотрим, например,
случай (б): т.к. λ
+ μ
> 0, то (λ
+ μ) ↑↑
↑↑ ,λ
,λ ↑↑
↑↑ ,μ
,μ ↑↓
↑↓
 ,
т.е. μ
,
т.е. μ ↑↓λ
↑↓λ .
.
Поэтому вектор
 коллинеарен как
коллинеарен как ,
так и
,
так и ,
и направлен в сторону более
,
и направлен в сторону более
длинного вектора,
т.е.
 .
.
 (14.10)
(14.10)
Из случая (б) имеем:
 ,
т.е.
,
т.е.
из (14.10) следует
 (14.11)
(14.11)
т.е. векторы
 и
и имеют одинаковую длину.
имеют одинаковую длину.
Заметим, что
 ,
ибо
,
ибо имеет большую длину, чем
имеет большую длину, чем
Поэтому

 и случай б) доказан
и случай б) доказан
(Остальные случаи читателю предоставим рассмотреть самостоятельно.)
Заметим, что
 (14.12)
(14.12)
 т.е.
(см 14.12));
т.е.
(см 14.12));
 (14.13)
(14.13)
Покажем, что (14.14)
(14.14)
Для чего рассмотрим следующие случаи:
а)
 б)
б) в)
в) г)
г)
Рассмотрим, например, случай (в) (остальные случаи просим читателя рассмотреть самостоятельно):
 и потому
и потому
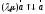 (14.15)
(14.15)
также
 ,
, ,
т.е.
,
т.е. (14.16)
(14.16)
сопоставляя (14.15) и (14.16), получим (14.14).
8)
 и
и ,
т.е.
,
т.е.
15 Вопрос а) Линейно – зависимые векторы и их свойства
Определение:
Система векторов
 называетсялинейно-зависимой
(л.з.),
если
называетсялинейно-зависимой
(л.з.),
если
 ,
не все из которых = 0 и
,
не все из которых = 0 и .
.
Определение:
 линейно выражается
через
линейно выражается
через
 ,
если
,
если ,
что
,
что
Свойства:
1) Если
система содержит нуль-вектор, то она
линейно зависима:
 =
=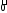 .
.
2) Если система имеет линейно зависимую подсистему, то она линейно зависима.

 ,
т.к.
,
т.к.

3) Система векторов линейно зависима, тогда и только тогда, когда хотя бы один вектор системы линейно выражается через остальные векторы.
 ,
если
,
если
 ,
то
,
то
Если же
 ,
то
,
то и система
и система линейно зависима.
линейно зависима.
