12 Вопрос

Ступенчатые матрицы и их ранг

12.1 Определение ступенчатой матрицы

Как было упомянуто раньше (см. п.9.3;определение 9.5), ступенчатой называется матрица такого вида:

.

Ранг ступенчатой матрицы

Имеет место теорема: ранг ступенчатой матрицы равен числу её ненулевых строк.

Теорема достаточно очевидна (в 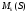надо удалить выделенные столбцы и строки)

13 вопрос

Теорема Кронеккер-Капелли

Формулировка теоремы Кронеккер-Капелли

Для того, чтобы система линейных уравнений была совместна, необходимо и достаточно, чтобы ранг её основной матрицы был равен рангу её расширенной матрицы.

(13.1)

;

Формулировка критерия определенности

Теорема (будет доказана в конце §19): Система линейных уравнений (13.1) определена (имеет единственное решение) тогда и только тогда, когда ранг её матрицы равен рангу её расширенной матрицы и равен числу неизвестных.

Доказательство необходимости теоремы Кронеккер-Капелли

(её достаточность будет доказана в конце §19)

Отметим, что r(B)≥r(A), ибо если r(B)=k, то всякий . Но всякийявляется минором матрицы В (ибо матрица А является частью матрицы В), и поэтому. Поэтому по лемме №2 из §11r(А)≤k=r(В).

Итак, пусть r(А)r(В)=k (тогда r(А)<r(B)). Приведя матрицу В к ступенчатому виду, получим: (подбудем обозначать преобразованные элементы матрицы А, а под– преобразованные элементы последнего столбца матрицы В).

При этом (k+1)-я строка матрицы В соответствует уравнению: 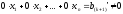, которое противоречиво, и, следовательно, система (13.1) несовместна.

Итак, если r(A)r(B), то, система (13.1) несовместна, и поэтому для совместности системы линейных уравнений (13.1) должно быть выполнено r(А)=r(В).

Необходимость теоремы Кронеккер-Капелли доказана.

14 Вопрос

А) вектор как направленный отрезок

Длина отрезка |АВ| - длина вектора

Под вектором обычно понимается величины , для задания которых необходимо знать не только их численное значение, но и направленное действие (Например, перемещение точки, скорость, ускорение, сила).

Величины для задания которых достаточно знать лишь их численное значение (например температура), называются скалярными величинами или скалярами. Обычно вектор обозначают как направленный отрезок.

А В

Определение: Система векторов называетсяколлинеарной, а эти векторы называются коллинеарными, если они лежат на одной прямой или на параллельных прямых.

1) 2)

В первом случае векторы коллинеарны, во втором – сонаправлены.

Определение: Система компланарная, а векторы – компланарные, если векторы находятся в одной плоскости или на параллельных плоскостях.

(Два вектора всегда компланарны.)

Определение: - нуль-вектор:

(Вектор, у которого конец и начало совпадают – нуль-вектор)

Этот вектор не имеет направления и коллинеарен любому вектору.

Свойства:

1.

2. Если , то

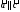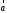3. , ,≠0 →

Определение: Векторы равные, если:

1. они коллинеарные

2. равны по длине

3. направлены в одну сторону

Определение: Если векторы коллинеарны, равны по длине, направлены в разные стороны, то они противоположные.

Определение: Множество всех векторов, равных заданному, называется свободным векторам.

Б)