9 Вопрос

Понятие элементарного преобразования

Элементарным преобразованием строк 1-го типа называется:

либо 1) замена строк местами;

либо 2) умножение строки на число ;

либо 3) сложение строк.

Элементарным преобразованием строк 2-го типа называется 1 из 2-х действий:

либо 1) замена строк местами;

либо 2) прибавление к одной строке другой, умноженной на некоторое число.

Аналогично определяются элементарные преобразования столбцов 1-го и 2-го типа.

Эквивалентные матрицы и системы

Матрицы А и В называются эквивалентными, если одну из них можно получить из другой с помощью конечного числа элементарных преобразований строк.

Соответственно различают эквивалентности первого и второго типа.

Системы линейных уравнений называются эквивалентными, если эквивалентны их расширенные матрицы.

Свойства:

1. А~А /рефлексивность/

2. А~ВВ~А /симметричность/

3. А~В, В~СА~С /транзитивность/

Ступенчатые матрицы; сведение матрицы к ступенчатой

Ступенчатой называется матрица такого вида:

/при переходе к следующей строке «вниз» идем не более, чем на один ненулевой элемент; слева направо последующая строка может увеличиться и на несколько нулевых элементов/

Нулевая матрица, по определению, также является ступенчатой.

Справедлива следующая теорема Гаусса:

Всякая матрица эквивалентна некоторой ступенчатой матрице.

Эту теорему доказываем методом математической индукции по числу строк матрицы А:

1. n=2, т.е. ;

Не ограничивая общности, можно считать, что , ибо если, а, то меняем местами первую и вторую строки.

Из второй строки матрицы А вычтем первую, умноженную на . Получим:

—ступенчатая матрица.

2. Шаг индукции. Пусть .

Можно считать, что первый столбец матрицы А ненулевой, т.е. при некоторомj. Тогда, меняя, в случае необходимости первую и j-ую строки местами, получим, что (для новой матрицы). Вычитая изj-й строки (j=2,3,...,k,k+1) первую, умноженную на , получим:

––ступенчатая матрица.

Матрица, получившаяся в правом нижнем углу матрицы А, состоит из k строк, и поэтому она сводится к ступенчатой по индуктивному предположению.

Теорема Гаусса доказана.

Диагональные матрицы

Матрица называется диагональной, если все её элементы, стоящие вне главной диагонали, равны нулю.

Имеет место следующая теорема:

Всякая невырожденная матрица эквивалентна некоторой диагональной и единичной.

Теорему доказываем методом математической индукции по порядку матрицы.

1. База индукции: пусть n=2.

, т.е.

Из 1-ой строки вычитаем 2-ую, умноженную на – диагональная матрица.

2. Шаг индукции:

Заметим, что 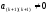(более того,для любогоj=1,2,…,k,k+1), ибо (см параграф 3 , п.3.3) . Тогда, вычитая изj-ой строки (k+1)-ю (j=1,2,…,k), умноженную на , получим, что:

(9.1)

.

матрица k-го порядка, которая, по индуктивному предположению, сводится к диагональной.

А поделив j-ю строку (j=1,2,…,k,k+1) на (как уже отмечалось ранее,для любогоj), получим единичную матрицу.

Теорема доказана.

10 Вопрос (Метод Гаусса) Решение произвольной системы линейных уравнений

Системы линейных уравнений называются эквивалентными, если эквивалентны их расширенные матрицы.

Метод Гаусса заключен к сведению расширенной матрицы к ступенчатой.

Рассмотрим его на примере, решая следующую систему:

1) Из второй строки вычтем утроенную первую, а из третьей – удвоенную первую;

2) вторую строку поделим на «-11», а третью – на «-3»;

3) к третьей строке прибавим вторую.

Обратный ход:

Матрица задает следующую систему уравнений

Тогда: ;и.