4 Вопрос

А)

Матрицей размера mn называется прямоугольная таблица чисел, состоящих из m строк и n столбцов.

Общий вид записи: А==

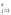
Матрицы называются равными, если они одного порядка и все элементы, стоящие на одних местах, совпадают.

А=; В=; А=В.

Замена строк столбцами, а столбцов – строками называется транспонированием матрицы.

Запись: А— матрица, транспонированная к матрице А, если А=, то А=.

Сложение матриц

Сложение матриц производится с матрицами одного порядка.

Определение: Если А= , В=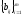,то матрицей А+В будет матрица , а матрицей –матрица .

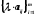
Свойства сложения матриц и умножения матрицы на число:

1. А+В=В+А;

2.(А+В)+С=А+(В+С);

3.Матрица, состоящая из одних нулей, называется нулевой матрицей,

тогда А+0=А ;

4.А (–А) | А+(–А)=0;

Матрица «–А» называется матрицей, противоположной матрице А. Она получается из матрицы А заменой знаков во всех её элементах на противоположные.

По определению, разностью матриц А и В является матрица А–В=А+(–В).

5.(А+В)=А+В;

6.;

7.;

8.;

9.Транспонирование суммы равно сумме транспонирований: (А+В) =А+В;

10.;

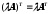Транспонированная матрица - матрица A^T, полученная из исходной матрицы A заменой строк на столбцы.

Формально, транспонированная матрица для матрицы A размеров — матрицаA^T размеров , определённая какA^T[i, j] = A[j, i].

Например,

и     

Б) Умножение матриц

Отметим, что число столбцов первого множителя А должно совпадать с числом строк второго множителя В (иначе произведение АВ не определено).

Тогда произведением матриц А и В является матрица С, число строк которой совпадает с числом строк первого множителя (матрицы А), а число столбцов ­– с числом столбцов второго множителя (матрицы В)

С=АВ; С:mn; ,и элементы которой определяются по формуле:

Свойства умн. Матриц

1., т.е. произведение матриц не коммутативно.

2.Произведение матриц ассоциативно: .

3. (правая дистрибутивность)

4. определитель произведения матриц равен произведению определителей: det(AB)=detAdetB.

5. транспонирование произведения матриц равно произведению транспонированных матриц, взятых в обратном порядке, т.е.

6.(левая дистрибутивность)

7. ; (Е - единичная матрица)

8.

5. Вопрос

Пусть А=­– квадратная матрица.

Определение: матрица называетсяобратной к матрице А, если выполнено равенство . Отметим, что вырожденная матрица обратной иметь не может, ибо если detA=0 , (противоречие).

Всякая невырожденная матрица А=имеет обратную матрицу= =, элементы которой находят по формуле: (5.20)

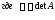, а – её алгебраические дополнения.

Свойства обратной матрицы:

для любых двух обратимых матриц A и B.

где * ^T обозначает транспонированную матрицу. для любого коэффициента.

Алгоритм нахождения обратной матрицы

чтобы найти обратную матрицу , нужно:

1. найти детерминант матрицы А; если он равен нулю, то обратной нет. Если detA0, то находим

2. матрицу из алгебраических дополнений;

3. транспонируем эту матрицу ;

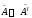4. всякий элемент матрицы делим наdetA, получим матрицу .