(47.20)

Общий вид двуполостного гиперболоида изображён на рис.47.7

Рис.47.8 Рис.47.9

При вращении гиперболы вокруг пересекающей её оси симметрии получится двуполостной гиперболоид вращения. (см. рис. 47.8)

В сечении двуполостного гиперболоида плоскостями могут получаться (см.рис 47.9, на котором гиперболоид и все секущие его плоскости изображены «сбоку»);

-эллипс(из рис.47.9 видно, что в сечении двуполостного гиперболоида плоскостью эллипс должна получиться некоторая ограниченная кривая второго порядка, т.е. эллипс);

-гипербола (согласно рис. 47.9, в сечении двуполостного гиперболоида плоскостью гипербола получается разрывная кривая второго порядка, т.е гипербола);

-парабола (получается в сечении двуполостного гиперболоида плоскостью, параллельной образующей его асимптотического конуса; читателю предлагаем самостоятельно из рис. 47.9 установить, что тогда в сечении возникает некоторая неограниченная непрерывная кривая второго порядка, т.е. парабола)

-одна точка (если секущая плоскость касается двуполостного гиперболоида);

-пустое множество (когда плоскость двуполостный гиперболоид не пересекает).

Остальные линии второго порядка в сечении двуполостного гиперболоида плоскостью получить нельзя.

В отличие от эллипсоидов, все виды которого можно перевести друг в друга (и, в том числе, и в сферу) с помощью некоторого линейного преобразования (например, непропорциального сжатия осей), однополостный и двуполостный гиперболоиды – совсем разные поверхности, которые нельзя перевести друг в друга никаким линейным преобразованием координат. Это , например, следует из того, что в сечении однополостного гиперболоида некоторой плоскостью можно получить две пересекающихся прямых линии, что нельзя сделать для двуполостного гиперболоида.

Более того, однополостный гиперболоид – связная (точнее, даже линейно связная) поверхность (т.е всякие две его точки можно соединить непрерывной линией, целиком лежащей на данной поверхности), а двуполостный гиперболоид связной поверхностью не являются.

Г) Эллиптический параболоид

Эллиптическим параболоидом называется поверхность, координаты всех точек которой в некоторой системе координат удовлетворяют уравнению:

(47.24)

Рис 47.10 Рис.47.11 Рис.47.12

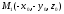Общий вид эллиптического параболоида изображён на рис.47.10, при этом начало координат (для уравнения (47.24)) будет вершиной параболоида, а ось аппликат OZ (являющаяся его осью симметрии, что легко проверить, ибо если точка лежит на эллиптическом параболоиде, т.е. её координатыудовлетворяют уравнению (47.24), то и координаты симметричной ей относительно оси аппликат точкитакже удовлетворяют уравнению (47.24), т.е. эта симметричная точка также находится на эллиптическом параболоиде)является осью эллиптического параболоида.

Эллиптический (точнее - круговой) параболоид вращения получится, если мы параболу будем вращать вокруг её оси симметрии (см.рис. 47.11)

В сечении эллиптического параболоида плоскостями могут получиться:

-парабола (если секущая плоскость параллельна оси параболоида или проходит через неё; исходя из рис.47.12 читателю предлагаем самостоятельно доказать, что в сечении эллиптического параболоида такой плоскостью будет некоторая неограниченная непрерывная кривая второго порядка, т.е. парабола);

-эллипс (когда секущая плоскость не параллельна его оси, пересекает, но не касается эллиптического параболоида; читателю предлагает показать самостоятельно, исходя из рис. 47.12, что в этом случае в сечении возникает некоторая ограниченная кривая второго порядка, т.е. эллипс);

- одна точка (если плоскость касается эллиптического параболоида);

-пустое множество (когда плоскость не пересекает эллиптический параболоид).

Остальные линии в сечении эллиптического параболоида плоскостями получить нельзя.

Д) Гиперболический параболоид

Гиперболический параболоидом называется поверхность, координаты всех точек которой в некоторой системе координат удовлетворяют уравнению.