Условие ортогональности и перпендикулярности прямых

. Для перпендикулярности прямых и(и)к последнему условию надо добавить также равенство (43.3).

44 Вопрос

А)

Взаимное расположение прямой и плоскости

Дано:

прямая

, ,(-направляющий вектор прямой, а- одна из её точек)

: ,(- нормаль к плоскости )

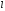
рис 44.1

Возможные случаи взаимного расположения прямой и плоскости

(т.е.,или;)(44.1)

; (44.2)

(есть одна точка) (44.3)

Б)

Угол между прямой и плоскостью. Условие их перпендикулярности

Заметим, что (см. рис. 44.2) Поэтому (см. формулу (24.11))

=

Мы показали

(44.4)

В частности .

П

рис 44.2

Точка пересечения прямой и плоскости

Если задано общее уравнение прямой

(37.3)

то для того, чтобы найти точку пересечения прямой с плоскостью

: Ax+By+Cz+D=0 (36.4)

надо уравнение плоскости приписать к системе уравнений (37.3) задающих прямую линию, и решить полученную систему из трёх линейных уравнений с тремя неизвестными. Решение этой системы и будет координатами точки пересечения прямойи плоскости.

Если прямая задана каноническим уравнением(40.2),

то для нахождения точки пересечения этой прямой с плоскостью , заданной уравнением (36.4), уравнение (40.2) целесообразно перевести в параметрическое уравнение той же прямой (см. §40).

(40.4)

Далее в линейное уравнение (36.4) вместо x, y ,z подставляем их выражения через параметр t по формуле (40.4). Получим некоторое линейное уравнение относительно t. Решим данное уравнение (относительно t), и найденное t подставим в формулу (40.4)Полученные после подстановки в (40.4) величины x, y, z и будут координатами точки пересечения прямой , заданной уравнением (40.2) или (40.4) и плоскостью(36.4)

В качестве примера рассмотрим задачу о том, как из точек на плоскость, заданную уравнением 36.4, опустить перпендикуляр (т.е. как найти проекцию точкина плоскость), а также докажем формулу (39.1) расстояния от точки до плоскости.

45 Вопрос Расстояние от точки до прямой в пространстве

Дано: точка M₁(x₁; y₁; z₁) и прямая (-одна из точек на прямойL). (-направляющий вектор прямойL)

Расстояние от точки M₁ до прямой L() совпадает с высотой () параллелограмма(см. рис 45.1), которая равна отношению площади () этого параллелограмма и длины основания. Далее у параграфов 25,26 и 24 (формула (24.10) имеем (см. также условие 2) векторное произведение.

|a|

(45.1)

46 Вопрос Расстояние между скрещивающимися прямым

и - направляющие векторы прямыхи, аи- некоторые из их точек.

Рассмотрим параллелепипед (см. рис. 46.1). Параллельные основания которогоипроходят через прямыеи. Тогда расстояние междуи() - это расстояние между вышеуказанными параллельными основаниями данного параллелепипеда, т.е. его высота (), опущенная на основание, равна отношению объёма данного параллелепипеда () к площади основания(), т.е. далее из §25(свойство 2) при определении векторного произведения, 26, 27 (см. чему равно абсолютная величина смешанного произведения), 28, 24(или формулы 21.2)) имеем:

(46.1)