
- •1 Вопрос Определители 2-го порядка
- •2 Вопрос Миноры и дополнения
- •3 Вопрос Определитель n-го порядка
- •3.1 Метод математической индукции
- •3.2 Вычисление определителя n-го порядка по минорам и ад
- •3.3 Верхне треугольный определитель
- •4 Вопрос
- •5. Вопрос
- •6 Вопрос. Системы линейных уравнений Определенность системы линейных уравнений. Совместность, несовместность (6.1)
- •Матричная форма записи m линейных уравнений с n неизвестными
- •9 Вопрос
- •Эквивалентные матрицы и системы
- •Ступенчатые матрицы; сведение матрицы к ступенчатой
- •10 Вопрос (Метод Гаусса) Решение произвольной системы линейных уравнений
- •11 Вопрос
- •12 Вопрос
- •14 Вопрос
- •Сложение векторов
- •Свойства линейного пространства
- •2) Ассоциативность
- •15 Вопрос а) Линейно – зависимые векторы и их свойства
- •Б) Формулировки теорем о линейной зависимости коллениарных и компланарных векторов
- •В) Формулировка теоремы о линейной зависимости четырех векторов.
- •16 Вопрос
- •19 Вопрос Исследование систем линейных уравнений Однородные системы
- •Решение неоднородных систем
- •Доказательство достаточности теоремы Кронеккер-Капелли
- •Доказательство критерия определённости системы
- •20 Вопрос
- •21 Вопрос
- •Свойства векторного произведения .(антикоммутативность, линейность и однородность)
- •Доказательство Леммы 25.1:
- •Векторное произведение базисных ортов
- •Свойства смешанного произведения
- •28 Вопрос Смешанное произведение векторов в координатной форме
- •36 Вопрос
- •Общее уравнение плоскости и его исследование
- •37 Вопрос Условия параллельности и перпендикулярности двух плоскостей, угол между ними Взаимное расположение двух плоскостей
- •Условие перпендикулярности
- •38 Вопрос
- •Уравнение плоскости, проходящей через три заданные точки
- •Уравнение плоскости в отрезках
- •39 Вопрос Расстояние от точки до плоскости
- •40 Вопрос Прямая как пересечение двух плоскостей. Общее уравнение прямой в пространстве
- •Каноническое уравнение прямой как уравнение прямой в пространстве проходящей через заданную точку и коллинеарной заданному вектору
- •Параметрическое уравнение прямой в пространстве
- •41 Вопрос Приведение общего уравнения прямой к каноническому виду
- •2) Найти направляющий вектор прямой .
- •Условие ортогональности и перпендикулярности прямых
- •44 Вопрос
- •Угол между прямой и плоскостью. Условие их перпендикулярности
- •Точка пересечения прямой и плоскости
- •45 Вопрос Расстояние от точки до прямой в пространстве
- •46 Вопрос Расстояние между скрещивающимися прямым
- •47 Вопрос
- •(47.17)
- •(47.31)
- •(47.18)
- •(47.20)
- •(47.24)
- •(47.25)
- •Эллиптический цилиндр
- •II. Гиперболический цилиндр
- •III. Параболический цилиндр
- •(47.32)
- •(35.21)
- •(47.36)
Каноническое уравнение прямой как уравнение прямой в пространстве проходящей через заданную точку и коллинеарной заданному вектору
Дано:
рис
40.1






 ,
Пусть M(x,y,z)
– точка прямой L
,
Пусть M(x,y,z)
– точка прямой L
Тогда
 ,
т.е. имеет место
,
т.е. имеет место

 уравнение:
уравнение:
 (40.2)
(40.2)
При этом даже может
и быть, например,
( =0,
=0, =0).
означает в (40.2), что
=0).
означает в (40.2), что
 .
Исключено лишь
.
Исключено лишь ,
ибо
,
ибо
Определение 40.1 . Уравнение (40.2) называется каноническим уравнением прямой в пространстве.
Параметрическое уравнение прямой в пространстве
Обозначим величину, стоящую в равенстве (40.2), за t. Получим уравнение
 (40.3)
(40.3)
Выразим x, y, z в (40.3) через t
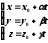 t
– параметр. (40.4)
t
– параметр. (40.4)
Если параметр t
принять за время, то уравнение (40.4) будет
задавать равномерное движение точки
M(x,y,z)
по прямой
 со скоростью
со скоростью
Определение 40.2. Уравнение (40.4) называется параметрическим уравнением прямой в пространстве.
41 Вопрос Приведение общего уравнения прямой к каноническому виду
Пусть задано общее уравнение прямой
 :
:
Условие (40.1) легко можно переписать в виде
 (41.1)
(41.1)
При этом прямая
 =
= ,
а плоскость
,
а плоскость и
и имеют нормали
имеют нормали

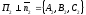
 ,
,

Чтобы общее уравнение прямой привести к каноническому, нужно:
Найти одну из точек на прямой

Для этого
надо выбрать в левой части неравенства
(41.1) ненулевой определитель (например,
 )
и положить в (37.3) переменную, которая не
соответствует выбранному определителю
(в нашем случае –z)
нулю или какому-либо иному числу. Тогда
система (37.3) станет системой с ненулевым
определителем (в нашем случае
)
и положить в (37.3) переменную, которая не
соответствует выбранному определителю
(в нашем случае –z)
нулю или какому-либо иному числу. Тогда
система (37.3) станет системой с ненулевым
определителем (в нашем случае
 ),
и, следовательно, она будет иметь
решение. Присоединив к этому решению
ранее выбранную величину (z),
получим координаты одной из точек на
прямой линии
),
и, следовательно, она будет иметь
решение. Присоединив к этому решению
ранее выбранную величину (z),
получим координаты одной из точек на
прямой линии
 .
.
2) Найти направляющий вектор прямой .
Так как
 и
и (
( ),
а
),
а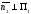 ,
и
,
и ,
то и
,
то и ,
,
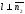 .
А так как вектор
.
А так как вектор
 также
также ,
и
,
и ,
то (см. задачу в п.29.1)
,
то (см. задачу в п.29.1) и поэтому
и поэтому Следовательно, направляющим вектором
прямой
Следовательно, направляющим вектором
прямой можно положить
можно положить
Пример:
привести к
каноническому виду

Решение:
1. х=0:


 ;
;
2. Направляющий
вектор
 ;
;
3. Уравнение
прямой:

42 вопрос
Уравнение прямой в пространстве, проходящей через две заданные точки
Дано

 Каноническое
уравнение
этой прямой имеет вид:
Каноническое
уравнение
этой прямой имеет вид:
 ;
(42.1)
;
(42.1)
а её параметрическое уравнение:
 (42.2)
(42.2)
Читателю предлагается
самостоятельно проверить, что координаты
точек
 и
и удовлетворяют как уравнению(42.1), так и
уравнению (42.2), при этом точек
удовлетворяют как уравнению(42.1), так и
уравнению (42.2), при этом точек в (42.2) соответствует значениеt=0
, а точке
в (42.2) соответствует значениеt=0
, а точке
 -t=1.
Эта прямая единственна как прямая,
проходящая через две заданные точки.
-t=1.
Эта прямая единственна как прямая,
проходящая через две заданные точки.
43 вопрос
А)
Взаимное расположение двух прямых в пространстве


 ,
,
 ,
,



 ,
,
 ,
,

Рассмотрим матрицы
 ;
;
 ;
;

рис.43.1
Возможные случаи взаимного расположения двух прямых:
r(А)=r(В)=1


 (43.1)
(43.1)
r(А)=1,
r(В)=2


 (43.2)
(см. рис 43.1)
(43.2)
(см. рис 43.1)
r(А)=r(В)=2
(43.3)

 ,
т.е. вектора
,
т.е. вектора ,
, и
и компланарны и не выполняются случаи
1)и 2)
компланарны и не выполняются случаи
1)и 2)
![]() пересекает
пересекает
 в единственной точке,
ибо случаи 1) и 2) исключают условие
(43.3). В частности
detB=0
в единственной точке,
ибо случаи 1) и 2) исключают условие
(43.3). В частности
detB=0

![]() и
и лежат в одной плоскости.
лежат в одной плоскости.
detB≠0
или r(А)=2,
r(В)=3

![]() и
и
 находятся в разных плоскостях или
скрещиваются.
(43.4)
находятся в разных плоскостях или
скрещиваются.
(43.4)
Б)
Угол между двумя
прямыми
 и
и можно найти как угол между их направляющими
векторами
можно найти как угол между их направляющими
векторами и
и ,
которые, согласно равенству (24.11) (см.§24),
можно найти по формуле:
,
которые, согласно равенству (24.11) (см.§24),
можно найти по формуле:
 (43.5)
(43.5)
