
- •1 Вопрос Определители 2-го порядка
- •2 Вопрос Миноры и дополнения
- •3 Вопрос Определитель n-го порядка
- •3.1 Метод математической индукции
- •3.2 Вычисление определителя n-го порядка по минорам и ад
- •3.3 Верхне треугольный определитель
- •4 Вопрос
- •5. Вопрос
- •6 Вопрос. Системы линейных уравнений Определенность системы линейных уравнений. Совместность, несовместность (6.1)
- •Матричная форма записи m линейных уравнений с n неизвестными
- •9 Вопрос
- •Эквивалентные матрицы и системы
- •Ступенчатые матрицы; сведение матрицы к ступенчатой
- •10 Вопрос (Метод Гаусса) Решение произвольной системы линейных уравнений
- •11 Вопрос
- •12 Вопрос
- •14 Вопрос
- •Сложение векторов
- •Свойства линейного пространства
- •2) Ассоциативность
- •15 Вопрос а) Линейно – зависимые векторы и их свойства
- •Б) Формулировки теорем о линейной зависимости коллениарных и компланарных векторов
- •В) Формулировка теоремы о линейной зависимости четырех векторов.
- •16 Вопрос
- •19 Вопрос Исследование систем линейных уравнений Однородные системы
- •Решение неоднородных систем
- •Доказательство достаточности теоремы Кронеккер-Капелли
- •Доказательство критерия определённости системы
- •20 Вопрос
- •21 Вопрос
- •Свойства векторного произведения .(антикоммутативность, линейность и однородность)
- •Доказательство Леммы 25.1:
- •Векторное произведение базисных ортов
- •Свойства смешанного произведения
- •28 Вопрос Смешанное произведение векторов в координатной форме
- •36 Вопрос
- •Общее уравнение плоскости и его исследование
- •37 Вопрос Условия параллельности и перпендикулярности двух плоскостей, угол между ними Взаимное расположение двух плоскостей
- •Условие перпендикулярности
- •38 Вопрос
- •Уравнение плоскости, проходящей через три заданные точки
- •Уравнение плоскости в отрезках
- •39 Вопрос Расстояние от точки до плоскости
- •40 Вопрос Прямая как пересечение двух плоскостей. Общее уравнение прямой в пространстве
- •Каноническое уравнение прямой как уравнение прямой в пространстве проходящей через заданную точку и коллинеарной заданному вектору
- •Параметрическое уравнение прямой в пространстве
- •41 Вопрос Приведение общего уравнения прямой к каноническому виду
- •2) Найти направляющий вектор прямой .
- •Условие ортогональности и перпендикулярности прямых
- •44 Вопрос
- •Угол между прямой и плоскостью. Условие их перпендикулярности
- •Точка пересечения прямой и плоскости
- •45 Вопрос Расстояние от точки до прямой в пространстве
- •46 Вопрос Расстояние между скрещивающимися прямым
- •47 Вопрос
- •(47.17)
- •(47.31)
- •(47.18)
- •(47.20)
- •(47.24)
- •(47.25)
- •Эллиптический цилиндр
- •II. Гиперболический цилиндр
- •III. Параболический цилиндр
- •(47.32)
- •(35.21)
- •(47.36)
Свойства векторного произведения .(антикоммутативность, линейность и однородность)
1.
 (антикоммутативность)
(антикоммутативность)
2.
 (однородность)
(однородность)
3.
 и
и
 (адютивность
(линейность))
(адютивность
(линейность))
Доказательство свойств:
1)

Доказательство:
 и
и и
и ,
а так же
,
а так же
 т.е.
т.е.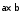 и
и ортогональны одним тем же плоскостям.
ортогональны одним тем же плоскостям.
Поэтому
 и(это мы определяем по правилу правой
руки)
и(это мы определяем по правилу правой
руки) ,
а
,
а (см. Рис25.1) следовательно
(см. Рис25.1) следовательно
2)

Доказательство:
Рассмотрим
следующие случаи
 ;
; ;
;
1)
 ,
,



Рис 25.2
 =
= ,
а так как
,
а так как ,
ибо они ортогональны плоскости
параллелограммаOADB
(см. рисунок 25.2), а так же они имеют
одинаковое направление ,что можно
определить направление по правилу
правой руки то
,
ибо они ортогональны плоскости
параллелограммаOADB
(см. рисунок 25.2), а так же они имеют
одинаковое направление ,что можно
определить направление по правилу
правой руки то

 >0
>0
2)


Рис 25.3
 (см. рис. 25.3)
(см. рис. 25.3)
 (25.1),
(25.1),
ибо
 и
и ортогональны одной и той же плоскости
параллелограммаOABD,
ортогональны одной и той же плоскости
параллелограммаOABD,
 (25.2)
(25.2)
 (25.3)
(25.3)
 ,
ибо эти параллелограммы имеют одинаковые
стороны
,
ибо эти параллелограммы имеют одинаковые
стороны
 и
и и общую высоту опущенную из вершиныB.
Поэтому из (25.2) и (25.3) следует , что:
и общую высоту опущенную из вершиныB.
Поэтому из (25.2) и (25.3) следует , что:

Читателю рекомендуем самостоятельно по правилу правой руки установить, то, что они направлены в разные стороны.
что
 и поэтому
и поэтому и случай
и случай доказан.
доказан.
3) тогда
тогда ,и
для
,и
для
можно применить случай 1). Из случаев 1)и 2) имеем:
(
(*)Свойство2)Для второго множителя можно доказать , используя уже доказанную антикоммутативность ( Свойство1)и только что полученное свойство2) для первого множителя:

3)
 ,
Рассмотрим следующие случаи:
,
Рассмотрим следующие случаи:
А) ,
,

Рис 25.4
Пололожим
 ,
, ,
, ;
аналогично
;
аналогично
 (25.7)
(25.7)
Тогда сумма
 диагональ параллелограммаOACB
(25.4)
диагональ параллелограммаOACB
(25.4)
 (25.5)
(25.5)
Также :
 и
и по определению векторного произведения
, и
по определению векторного произведения
, и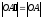 и
и (см 25.7)тогда параллелограмм
(см 25.7)тогда параллелограмм получится из параллелограммаOACB
поворотом последнего на угол
получится из параллелограммаOACB
поворотом последнего на угол
 (
по часовой стрелке). Поэтому и диагональ
(
по часовой стрелке). Поэтому и диагональ
 и
и
 =
= (напомним,
что
(напомним,
что и
и , т.е.
, т.е.
 (25.6)
(25.6)
Подставляя в (25.6)
вместе
 и
и их значения из формулы (25.4) и (25.6) получим
их значения из формулы (25.4) и (25.6) получим


случай А) доказан
Б)
 введем вектор
введем вектор

условию А) поэтому

, и случай Б доказан
В дальнейшем случае нам понадобится Лемма25.1:
Обозначим за проекцию вектора
проекцию вектора на плоскость , перпендикулярную вектору
на плоскость , перпендикулярную вектору (эта
проекция сама является вектором, которая
на рис 25.5 обозначим за
(эта
проекция сама является вектором, которая
на рис 25.5 обозначим за ).
).
Тогда имеет равенство:
 (25.8)
(25.8)
Доказательство Леммы 25.1:

Рис 25.5
 (
см. рис 25.5). Поэтому
(
см. рис 25.5). Поэтому
 ортогональна
той же плоскости параллелограммаOACB
(см. рис 25.5 где вектор
ортогональна
той же плоскости параллелограммаOACB
(см. рис 25.5 где вектор
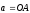 ).
Поэтому они коллинеарные и по правилу
правой руки определяем ,что
).
Поэтому они коллинеарные и по правилу
правой руки определяем ,что
 (25.9)
(25.9)
Их длины (25.10)
(25.10)
 (25.11)
(25.11)
Но параллелограмм
OACB
и прямоугольник
 имеет одинаковые площади, ибо они имеют
общую сторонуOA
и одинаковую высоту( эта высота равна
AD).
имеет одинаковые площади, ибо они имеют
общую сторонуOA
и одинаковую высоту( эта высота равна
AD).
Поэтому из (25.10) и (25.11) получаем , что
 (25.12)
(25.12)
Тогда из (25.12) и
(25.9) получим , что

Для доказательства правой части (25.8) можно использовать антикоммутативность и только что полученное равенство.

Лемма 25.1 доказана.
Продолжим доказательство свойства 3
В)
Так как
 и
и ,
то вектора
,
то вектора ,
, и
и удовлетворяют
уже доказанному свойству Б. А так как
проекция суммы равна сумме проекций(
это было доказано в §20), т.е из Леммы 25.1
получим :
удовлетворяют
уже доказанному свойству Б. А так как
проекция суммы равна сумме проекций(
это было доказано в §20), т.е из Леммы 25.1
получим :

Для доказательства
равенства
 используем антикоммутативность
векторного произведения и только что
доказанное равенство:
используем антикоммутативность
векторного произведения и только что
доказанное равенство:
 .
.
Свойство 3 полностью доказано.
Условие коллинеарности двух векторов
Из условия 2 при определении векторного произведения получаем , что
 (25.13)
(25.13)
( ибо если
 ,
параллелограмм
OADB
(см.рис 25.1) будет иметь нулевую площадь
и наоборот)
,
параллелограмм
OADB
(см.рис 25.1) будет иметь нулевую площадь
и наоборот)
