
- •1 Вопрос Определители 2-го порядка
- •2 Вопрос Миноры и дополнения
- •3 Вопрос Определитель n-го порядка
- •3.1 Метод математической индукции
- •3.2 Вычисление определителя n-го порядка по минорам и ад
- •3.3 Верхне треугольный определитель
- •4 Вопрос
- •5. Вопрос
- •6 Вопрос. Системы линейных уравнений Определенность системы линейных уравнений. Совместность, несовместность (6.1)
- •Матричная форма записи m линейных уравнений с n неизвестными
- •9 Вопрос
- •Эквивалентные матрицы и системы
- •Ступенчатые матрицы; сведение матрицы к ступенчатой
- •10 Вопрос (Метод Гаусса) Решение произвольной системы линейных уравнений
- •11 Вопрос
- •12 Вопрос
- •14 Вопрос
- •Сложение векторов
- •Свойства линейного пространства
- •2) Ассоциативность
- •15 Вопрос а) Линейно – зависимые векторы и их свойства
- •Б) Формулировки теорем о линейной зависимости коллениарных и компланарных векторов
- •В) Формулировка теоремы о линейной зависимости четырех векторов.
- •16 Вопрос
- •19 Вопрос Исследование систем линейных уравнений Однородные системы
- •Решение неоднородных систем
- •Доказательство достаточности теоремы Кронеккер-Капелли
- •Доказательство критерия определённости системы
- •20 Вопрос
- •21 Вопрос
- •Свойства векторного произведения .(антикоммутативность, линейность и однородность)
- •Доказательство Леммы 25.1:
- •Векторное произведение базисных ортов
- •Свойства смешанного произведения
- •28 Вопрос Смешанное произведение векторов в координатной форме
- •36 Вопрос
- •Общее уравнение плоскости и его исследование
- •37 Вопрос Условия параллельности и перпендикулярности двух плоскостей, угол между ними Взаимное расположение двух плоскостей
- •Условие перпендикулярности
- •38 Вопрос
- •Уравнение плоскости, проходящей через три заданные точки
- •Уравнение плоскости в отрезках
- •39 Вопрос Расстояние от точки до плоскости
- •40 Вопрос Прямая как пересечение двух плоскостей. Общее уравнение прямой в пространстве
- •Каноническое уравнение прямой как уравнение прямой в пространстве проходящей через заданную точку и коллинеарной заданному вектору
- •Параметрическое уравнение прямой в пространстве
- •41 Вопрос Приведение общего уравнения прямой к каноническому виду
- •2) Найти направляющий вектор прямой .
- •Условие ортогональности и перпендикулярности прямых
- •44 Вопрос
- •Угол между прямой и плоскостью. Условие их перпендикулярности
- •Точка пересечения прямой и плоскости
- •45 Вопрос Расстояние от точки до прямой в пространстве
- •46 Вопрос Расстояние между скрещивающимися прямым
- •47 Вопрос
- •(47.17)
- •(47.31)
- •(47.18)
- •(47.20)
- •(47.24)
- •(47.25)
- •Эллиптический цилиндр
- •II. Гиперболический цилиндр
- •III. Параболический цилиндр
- •(47.32)
- •(35.21)
- •(47.36)
Доказательство достаточности теоремы Кронеккер-Капелли
Полагая в системе
(19.2): Ax
= b
все свободные неизвестные нулями,
получим систему:
 (19.18),
(19.18),
где
 –
матрица базисного минора. А так как это
матрица невырожденная, то система
(19.18) (и система (19.2)) имеет решение.
–
матрица базисного минора. А так как это
матрица невырожденная, то система
(19.18) (и система (19.2)) имеет решение.
Доказательство критерия определённости системы
Если n = r , то по теореме 19.2 множество решений однородной системы (19.7) имеет размерность, равную нулю, то есть решение однородной системы состоит только из одного нулевого решения. Тогда, по теореме 19.3 всякие решения системы (19.1) состоят только из одного частного решения, то есть оно единственно, и поэтому система (19.1) является определённой.
20 Вопрос
Базис - множество таких векторов в векторном пространстве, что любой вектор этого пространства может быть единственным образом представлен в виде линейной комбинации векторов из этого множества - базисных векторов.
Ортонормированный базис
Определение:
Векторы
 и
и –ортогональные,
если они перпендикулярны друг другу.
–ортогональные,
если они перпендикулярны друг другу.
Определение: Базис является ортогональным, если все его векторы попарно перпендикулярны.
Определение: Базис является ортонормированным, если он ортогонален и все векторы в нём имеют единичную длину.
Если базис
 ортонормированный, то
ортонормированный, то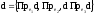
Где
 - проекция вектора
- проекция вектора на
вектор
на
вектор (для
вывода этой формулы надо внимательно
разобрать доказательства всех теорем
из §16.1, когда
(для
вывода этой формулы надо внимательно
разобрать доказательства всех теорем
из §16.1, когда
 -
ортонормированный базис ) для теорем
16.3, а так же
-
ортонормированный базис ) для теорем
16.3, а так же
 -ортонормированный
базис (для теорем 16.2) либо
-ортонормированный
базис (для теорем 16.2) либо для теорем 16.1
для теорем 16.1
Тогда из §17 получим
следующие свойства проекции вектора на вектор:















Рис 20.1
21 Вопрос
Прямоугольная декартова система координат. Координаты точки. Определение координат вектора по координатам его начала и конца. Расстояние между двумя точками
Координаты точки – это координаты вектора ОМ (где О –
начало координат
– это координаты вектора ОМ (где О –
начало координат
(см. рис 21.1)) ,
т.е.
,
т.е. (см. рис. 21.2)
(см. рис. 21.2)
тогда, если
 и
и ,z
,z
т.е.
 и
и ,
,
то
 y
y






x
Рис 21.1
В §24 будет показано,
что длина вектора

 (21.2)
(21.2)
Тогда расстояние между точками A и B:
 (21.3)
(21.3)
 (расстояние между
точками А и В – это длина вектора АВ)
(расстояние между
точками А и В – это длина вектора АВ)
23 вопрос
Скалярное произведение векторов и его свойства
Определение:
 (23.6) – скалярное
произведение
(23.6) – скалярное
произведение

Свойства скалярного произведения:
Величина
 называется
скалярным
квадратом
вектора
называется
скалярным
квадратом
вектора .
По определению:
.
По определению:
 (23.9)
(23.9)
Доказательство 2-го свойства:

Доказательство 3-го свойства:

Условие ортогональности 2-х векторов:
Если
 .
Вывод
.
Вывод .
.
24 вопрос
Вычисление скалярного произведения векторов через координаты сомножителей
Вычисление скалярного произведения через координаты сомножителей
Пусть



Ибо 1= и
и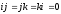 так как
так как

Тоесть
 (24.9)
(24.9)
Доказательство
формулы

Пусть
 ,тогда из(24.9)
имеем
,тогда из(24.9)
имеем
 (24.10)
(24.10)
Вычисление угла между векторами
 (24.11)
(24.11)
Смотрите формулы (23.6), (24.9), (24.10)
Проекция
вектора
 на ось, коллинеарную вектору
на ось, коллинеарную вектору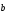
Смотрите формулы (23.6), (24.9), (24.10)
 ,
(24.12)
,
(24.12)
 =0 (24.13)
далее формула
=0 (24.13)
далее формула
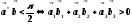 (либо в этом случае
(либо в этом случае
 ,далее формула (23.6))
,далее формула (23.6))
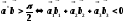 (здесь
уже
(здесь
уже
 , затем используем равенство (23.6)
, затем используем равенство (23.6)
25 вопрос
Векторное произведение и его свойства
Определение векторного произведения
Обозначение векторного произведения :
 при
этом , по определению.
при
этом , по определению.
1)
 ,
,
2)


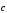
S-площадь
параллелограмма
OADB
B 

 D
D

О
 А
А
Рис 25.1
Направление
вектора определяется
по “правилу правой руки”: если большой
палец правой руки направлен по вектору
определяется
по “правилу правой руки”: если большой
палец правой руки направлен по вектору
 ,
а указательный по вектору
,
а указательный по вектору ,
то ладонь укажет направление векторного
произведения.
,
то ладонь укажет направление векторного
произведения.
Его также можно
определить по “правилу правого винта”
или “Буравчика”: векторное
произведение направленно в сторону
движения правого винта , если его вращать
от вектора
 к вектору
к вектору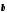 .
.




