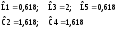3. Задание на курсовую работу.

Внимание! 1. Вариант задания определяется по двум последним цифрам номера студенческого билета: последняя цифра – N0; предпоследняя цифра – N1.

2. Рекомендуется для выполнения курсовой работы использовать «Образец синтеза фильтра» - файл, составленный в приложении MathCad. Файл размещён в электронной почте по адресу, который укажет преподаватель, проводящий занятия по ОТЦ.

Задание 1. Синтез двусторонне нагруженного фильтра нижних частот (на базе LC элементов).

Требования к характеристике рабочего ослабления и тип характеристики (Баттерворта или Чебышёва) синтезируемого фильтра определяется заданными в Таблице 3.1 значениями в зависимости от того, чётной или нечётной величиной является номер Вашего варианта N0.

1. Выполнить нормирование по частоте требуемой рабочей характеристики ослабления.

2. Рассчитать коэффициент ε и порядок ФНЧ (NБ или NЧ). Записать полином .

3. Рассчитать корни полинома Гурвица и записать полином .

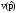4. Записать выражение и выполнить разложение в цепную дробь.

5. Рассчитать истинные значения параметров элементов схемы, выполнив денормирование по частоте и по сопротивлению. Начертить схему фильтра.

6. Рассчитать и построить графики рабочего ослабления и модуля рабочей передаточной функции.

Таблица 3.1.

	N0 – нечётная величина (1,3,5,7,9)	N0 – чётная величина (0,2,4,6,8)
Фильтр	с частотной характеристикой Баттерворта	с частотной характеристикой Чебышёва
Неравномерность ослабления ∆А, дБ	∆A = (2,75 - 0,25·N1), дБ	∆A = (0,5 + 0,25·N1), дБ
В полосе непро-пускания AS, дБ	As = (47 - 3·N1) , дБ	As = (20+5·N1), дБ
Граница полосы пропускания f1	(5+2·N0)·103 , Гц	(4+2·N0)·103 , Гц
Граница полосы непропускания f2	(15+4·N0)·103 , Гц	(14+4·N0)·103, Гц
Сопротивление нагрузки R2, Ом	R2 = (20+5·N1)·103 , Ом	R2 =(50+5·N1)·103, Ом

Задание 2. Синтез симметричного полосового фильтра (на базе LC элементов).

Требования к характеристике рабочего ослабления и тип характеристики (Баттерворта или Чебышёва) синтезируемого фильтра определяется заданными в Таблице 3.2 значениями.

1. Выполнить преобразование частотной переменной Ωп → Ωн.

2. Синтезировать ФНЧ-прототип.

3. Выполнить обратное преобразование частотной переменной для перехода от ФНЧ-прототипа к ПФ.

4. Рассчитать истинные значения параметров элементов схемы. Начертить схему фильтра.

5. Рассчитать и построить графики рабочего ослабления и модуля рабочей передаточной функции.

Таблица 3.2.

	N0 – нечётная величина (1,3,5,7,9)	N0 – чётная величина (0,2,4,6,8)
Фильтр	с частотной характеристикой Чебышёва	с частотной характеристикой Баттерворта
Неравномерность ослабления ∆А, дБ	∆A = (0,5 + 0,25·N1), дБ	∆A = (0,4 + 0,2·N1), дБ
В полосе непро-пускания AS, дБ	As = (35 - 0,5·N1), дБ	As = (20 + 0,5·N1), дБ
Нижняя граница полосы пропускания f1΄	(30 - 0,25·N0)·103, Гц	(65 - 0,25·N0)·103, Гц
Верхняя граница полосы пропускания f1	(40 + 0,5·N0)·103, Гц	(80 + 0,5·N0)·103, Гц
Верхняя граница полосы непропускания f2	(50 + 0,5·N0)·103, Гц	(100 + 0,5·N0)·103, Гц
Сопротивление нагрузки R2, Ом	R2 = (10 + 2·N1)·103, Ом	R2 = (600 + 20·N1)·103, Ом

Задание 3. Синтез активного фильтра нижних частот.

Требования к характеристике рабочего ослабления и тип характеристики (Баттерворта или Чебышёва) синтезируемого фильтра определяется заданными в Таблице 3.3 значениями.

1. Выполнить нормирование по частоте требований к рабочей характеристике ослабления.

2. Рассчитать коэффициент ε и порядок ФНЧ (NБ или NЧ). Записать полином .

3. Рассчитать корни полинома Гурвица и записать функцию .

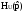4. Определить нормированные параметры элементов четырёхполюсников.

5. Рассчитать истинные значения параметров элементов схемы. Начертить схему фильтра. Рассчитать и построить графики рабочего ослабления и модуля передаточной функции по напряжению (для каждого четырёхполюсника в отдельности и для фильтра в целом).

Таблица 3.3.

	N0 – нечётная величина (1,3,5,7,9)	N0 – чётная величина (0,2,4,6,8)
Фильтр	с частотной характеристикой Баттерворта	с частотной характеристикой Чебышёва
Неравномерность ослабления ∆А, дБ	∆A = (2,8 - 0,2·N1), дБ	∆A = (0,5 + 0,25·N1), дБ
В полосе непро-пускания AS, дБ	As = (20 – 0,5·N1) , дБ	As = (15 + 2,5·N1), дБ
Граница полосы пропускания f1	(30 + 1·N0)·103 , Гц	(10 + 0,5·N0)·103 , Гц
Граница полосы непропускания f2	(80 – 0,5·N0)·103 , Гц	(20 + 0,5·N0)·103, Гц
Коэффициент усиления К	12 – 0,25·N1	6 + 0,5·N1

4. МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО РАСЧЁТУ ФИЛЬТРОВ.

1. СИНТЕЗ ДВУСТОРОННЕ НАГРУЖЕННОГО ФИЛЬТРА НИЖНИХ ЧАСТОТ.

Для выполнения этого задания необходимо изучить соответствующие разделы по рекомендованной литературе. Желательно использовать файл, содержащий пример синтеза ФНЧ, разработанный в приложении MathCad. В Таблице 4.1 приведены расчёты, выполненные при синтезе ФНЧ с характеристиками Баттерворта и Чебышёва. Вычисления выполнены с применением методического материала из раздела 2 и файла, разработанного в приложении MathCad.

Задание. Синтезировать двусторонне нагруженные ФНЧ с характеристиками Баттерворта и Чебышёва, удовлетворяющие следующим требованиям:

∆А = 2 дБ; Аs = 20 дБ; f­₁= 500 Гц; f₂= 900 Гц; R2 = 1000 Ом.

Таблица 4.1.

ФНЧ с характеристикой Баттерворта.	ФНЧ с характеристикой Чебышёва.
Нормирование по частоте и сопротивлению: Ω1 = f1/f1=1; Ω2 = f2/f1=1,8;
Коэффициент неравномерности: ;
Корни полинома Гурвица:	;
Полином Гурвица:
Степенной полином: Числитель функции фильтрации:	Полином Чебышёва:
Входное сопротивление: (примем )
После разложения в цепную дробь получа-ется схема (рис. 2.3) с тремя индуктивными и двумя емкостными элементами: Целесообразно перейти к дуальной схеме:	После разложения в цепную дробь получа-ется схема с двумя индуктивными и одним емкостным элементом: Целесообразно перейти к дуальной схеме:
Денормированные параметры:
Расчёт рабочего ослабления и рабочей передаточной функции. Графики функций представлены на рисунке 4.1.

Рабочее ослабление и модуль рабочей передаточной функции ФНЧ с характеристикой Баттерворта:

_; ,

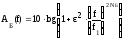Рабочее ослабление и модуль рабочей передаточной функции ФНЧ с характеристикой Чебышёва:

,

.

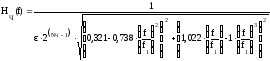Рис. 4.1.

Обратите внимание на то, что порядок Nч численно совпадает с количеством экстремумов частотных характеристик Чебышёва в полосе пропускания.

2. СИНТЕЗ ПОЛОСОВОГО ФИЛЬТРА С СИММЕТРИЧНОЙ ХАРАКТЕРИСТИКОЙ.

Для выполнения этого задания необходимо изучить соответствующие разделы по рекомендованной литературе и использовать файл, содержащий пример синтеза ПФ.

Задание. Синтезировать симметричный ПФ с характеристикой Чебышёва, удовлетворяющий следующим требованиям:

∆А = 0,5 дБ; Аs = 16 дБ; f­₁΄= 8000 Гц; f₁= 12500 Гц; f₂= 16000 Гц; R2 = 1000 Ом.

1. Определение дополнительных параметров:

ширина полосы пропускания ∆f = f₁ – f₁΄ = 4500 Гц; средняя частота ; нижняя граничная частота полосы непропускания f₂΄ = (f₀)²/f₂ = 6250 Гц; коэффициент неравномерности ε = 0,349.

2. Преобразование частотной переменной в соответствии с формулами (2.28):

; - граничная частота полосы непропускания фильтра-прототипа нижних частот.

2. Определение порядка ФНЧ-прототипа с характеристикой Чебышёва:

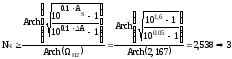
3. Синтез нормированного ФНЧ-прототипа.

3.1. Корни полинома Гурвица

3.2. Полином Гурвица

3.3. Числитель функции фильтрации

3.4. Нормированная функция входного сопротивления ФНЧ-прототипа

После разложения в цепную дробь получается схема с двумя индуктивными и одним емкостным элементом:

4. От схемы ФНЧ-прототипа перейти к схеме ПФ с нормированной характеристикой путём замены каждого индуктивного элемента в продольной ветви на последовательное соединение индуктивного и емкостного элементов с параметрами

;;

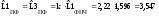и замены каждого емкостного элемента в поперечной ветви на параллельное соединение индуктивного и емкостного элементов с параметрами (рис. 2.12)

.

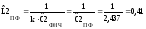5. Выполнить денормирование параметров элементов:

,

.

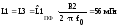
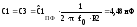6. Рассчитать рабочее ослабление A(f) и построить график (рисунок 4.2):

График функции, представленный на рисунке 4.2, имеет левую и правую ветви, геометрически симметричные относительно частоты f₀. Обратите внимание на то, что порядок фильтра (Nч = 3) численно совпадает с количеством экстремумов правой и левой ветвей функции в полосе пропускания; одна точка экстремума на частоте f₀ – общая для обеих ветвей.

3. СИНТЕЗ АКТИВНОГО ФИЛЬТРА НИЖНИХ ЧАСТОТ.

Для выполнения этого задания необходимо изучить соответствующие разделы по рекомендованной литературе и использовать файл, содержащий пример синтеза АRC ФНЧ.

Задание. Синтезировать активный ФНЧ с характеристикой Чебышёва, удовлетворяющий следующим требованиям:

∆А = 1 дБ; Аs = 14 дБ; f₁= 20000 Гц; f₂= 35000 Гц; К = 9 (коэффициент усиления).

1. Нормирование по частоте и сопротивлению: Ω₁ = f₁/f₁=1; Ω₂ = f₂/f₁=1,75; .

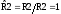_{2. Порядок ФНЧ:} ,

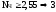
3. Корни полинома Гурвица:

;

4. Активный фильтр третьего порядка может быть реализован с применением двух активных четырёхполюсников – второго и первого порядков (рис. 4.3). Передаточная функция по напряжению может быть получена с применением формул (2.29) и (2.30):

где К = К1·К2 = 9; выбираем произвольно (К2 > К1): К2 = 4,5 и К1 = 2.

Рис. 4.3.

5. Четырёхполюсник 2-го порядка. Передаточная функция по напряжению

В выражении передаточной функции заданы значения трёх коэффициентов, требуется определить пять нормированных параметров схемы. Значения двух параметров задаём произвольно. Желательно, чтобы все нормированные параметры были бы одного порядка.

Пусть ; тогда из условия следует: .

Пусть ; тогда из условияследует:.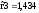

Из условия 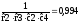следует:.

Для денормирования параметров элементов используется частота среза f_c = 21900 Гц; денормированные значения резистивных сопротивлений выбираются произвольно, учитывая, что наиболее приемлемые величины – от нескольких до ста килом. Например,

r1 = 20 кОм; r2 = 22,5 кОм; r3 = 14,34 кОм;

пФ; пФ;

6. Четырёхполюсник 1-го порядка. Передаточная функция по напряжению

Пусть ; тогда из условия следует: .

Пусть ; тогда из условия следует: .

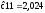Денормирование параметров: r11 = r21 = r31 = 20 кОм, пФ.

7. Расчёт частотных характеристик.

Передаточная функция по напряжению для четырёхполюсника второго порядка:

;

Передаточная функция по напряжению для четырёхполюсника первого порядка:

;

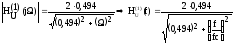Передаточная функция по напряжению для фильтра в целом:

.

Рабочее ослабление для каждого четырёхполюсника и для фильтра в целом:

дБ; дБ;дБ.

Графики рабочего ослабления и модуля рабочей передаточной функции для каждого четырёхполюсника в отдельности и фильтра в целом представлены на рисунке 4.4.

5. ВОПРОСЫ ДЛЯ ПОДГОТОВКИ К ЗАЩИТЕ КУРСОВОЙ РАБОТЫ.

1. Дайте определение электрического фильтра.

2. Как классифицируются фильтры по типу частотной обработки передаваемого сигнала?

3. На какие области разделяется весь частотный диапазон фильтров? Дайте определение каждой из них.

4. Что называется рабочей передаточной функцией четырёхполюсника?

5. Укажите условия физической реализуемости фильтра. Какие полиномы называются полиномами Гурвица?

6. Что называется порядком фильтра? Какая связь между порядком фильтра и числом реактивных элементов?

7. Что значит осуществить нормирование по частоте; по сопротивлению? В чём сущность денормирования?

8. Какие схемы называются дуальными?

9. Какие фильтры являются полиномиальными?

10. Начертите графики зависимостей функции рабочего ослабления А(Ω) и модуля рабочей передаточной функции Н(Ω) от нормированной частоты Ω для ФНЧ с плоской характеристикой (фильтра Баттерворта). В чём заключается влияние порядка фильтра N на вид этих характеристик?

11. Начертите графики А(Ω) и Н(Ω) для ФНЧ с равноволновой характеристикой (фильтра Чебышёва). Каково влияние порядка фильтра N на вид этих характеристик?

12. В чём заключается сущность метода преобразования частотной переменной? Как перейти от НЧ-прототипа к ФВЧ? К полосовому фильтру?

13. Какой ПФ называются фильтром с геометрически симметричной характеристикой? Что называется средней частотой ПФ?

14. Что называется частотой среза? Как вычислить частоту среза?

15. Какие фильтры называются активными? Из каких элементов состоят ARC-фильтры?

16. Какое свойство четырёхполюсников на базе операционных усилителей обеспечивает возможность синтеза ARC фильтра в целом путём расчёта каждого из каскадно-соединённых звеньев в отдельности?

CОДЕРЖАНИЕ
1. Общие замечания …………………………………….……………………………………			3
Список литературы ………………………………………………………………………...			3
Требования к оформлению курсовой работы ……………………………………….....			3
2. Методические указания по изучению раздела курса ………………………….……….			4
	2.1. Основы синтеза фильтров по рабочим параметрам ..………………..………. 2.2. Нормирование по сопротивлению и частоте ……………………..………..…		5 8
	2.3. Построение дуальных схем …………………………………………………….…		9
	2.4. Аппроксимация частотных характеристик ……………………….………………		9
	2.5. Реализация аппроксимирующей функции электрической цепью …………..		13
	2.6. Метод преобразования частотной переменной ……………………………….		13
	2.7. Активные фильтры ……………………………………………………………..		15
3. Задание на курсовую работу …………………………………………………………….			18
4. Методические указания по расчёту фильтров ……………………………………………			20
5. Вопросы для подготовки к защите курсовой работы …………………………………..			26
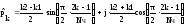
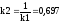
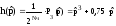