2.4.2. Аппроксимация по критерию Чебышёва.

При использовании для аппроксимации по Тейлору степенных полиномов Ω^2·NБ получается хорошее приближение к идеальной функции вблизи точки Ω=0, но для того чтобы обеспечить достаточную крутизну аппроксимирующей функции при Ω>1 приходится увеличивать порядок полинома (а, следовательно, и порядок схемы).

Лучшую крутизну в переходной области частот можно получить, если в качестве аппроксимирующей выбрать не монотонную функцию (рис. 2.4), а функцию колеблющуюся в диапазоне значений 0 … ΔА в полосе пропускания при 0<Ω<1 (рис. 2.7).

Наилучшая аппроксимация по критерию Чебышёва обеспечивается применением полиномов Чебышёва P_N(x) (рис. 2.6). В интервале -1 < x < 1 отклонения аппроксимирующих функций от нулевого уровня равны ±1 и чередуются по знаку.

В интервале -1 < x < 1 полином Чебышёва порядка N описывается выражением

P_N(x) = cos(N·arccos(x))_, (2.21)

при N=1 P₁(x) = cos(arccos(x)) = x,

при N=2 P₂(x) = cos(2·arccos(x)) = 2· cos²(arccos(x)) – 1 = 2·x² – 1,

при N≥3 полином P_N(x) можно вычислить, пользуясь рекуррентной формулой

P_N+1(x) = 2·х·P_N(x) - P_N-1(x).

При x > 1 значения полиномов Чебышёва монотонно возрастают и описывается выражением

P_N(x) = ch(N·Arch(x)). (2.22)

Функция рабочего ослабления (рис. 2.7) описывается выражением

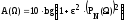, (2.23)

где ε – коэффициент неравномерности, определяемый по формуле (2.17);

- квадрат модуля функции фильтрации;

P_N(Ω) – полином Чебышёва порядка N.

Рабочее ослабление в полосе непропускания должно превышать значение A_S:

.

Подставив в это неравенство выражение (2.22) для значений частот полосы непропускания, решим его относительно величины N = NЧ - порядка полинома Чебышёва:

. (2.24)

Порядок полинома должен быть целым числом, поэтому получившееся значение необходимо округлить до ближайшего большего целого значения.

Квадрат модуля рабочей передаточной функции (нормированное значение)

. (2.25)

Поскольку нули ослабления (они же – корни полинома Гурвица) располагаются в полосе пропускания, в это выражение надо подставить выражение (2.21) для значений частот полосы пропускания.

Выражение (2.25) представим в операторной форме, используя преобразование jΩ→:

Корни полинома определяются по формуле:

k = 1, 2, … , NЧ, (2.26)

где .

Комплексно-сопряжённые корни в комплексной плоскости располагаются на эллипсе. Полином Гурвица образуют только корни с отрицательной реальной составляющей:

.

Квадрат модуля функции фильтрации ; поэтому полином находимсприменениемрекуррентнойформулы:

; ;;.

является полиномом с вещественными коэффициентами; является полиномом чётной степени. Условия физической реализуемости выполняются.

2.5. Реализация аппроксимирующей функции электрической цепью.

Один из методов решения задачи реализации основан на разложении в цепную дробь функции входного сопротивления

.

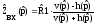Процедура разложения описана в литературе: [1, глава 16], [2, глава 20] [3, глава 15]. Кратко пояснить разложение в цепную дробь можно следующим образом.

Функция представляет собой отношение полиномов. Сначала выполняется деление полинома числителя на полином знаменателя; затем полином, который был делителем, становится делимым, а полученный остаток становится делителем, и так далее. Полученные при делении частные образуют цепную дробь. Для схемы на рисунке 2.8 цепная дробь имеет вид (при=1):

.

Если необходимо, можно от полученной

схемы перейти к дуальной.