Наращенная сумма и современная стоимость постоянной ренты постнумерандо (на примере годовой ренты)

Методом прямого счета, как это было рассмотрено выше, можно найти наращенную сумму и современную стоимость любого потока платежей. Однако удобнее воспользоваться более компактными формулами.

Пусть в течение лет в банк в конце каждого года вносится по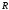рублей. На взносы начисляются сложные проценты по ставкегодовых. Т.о. имеется рента, член которой равен, а срок -. Все члены ренты, кроме последнего, приносят проценты – на первый член проценты начисляютсягод, на второйи т.д. На последний взнос проценты не начисляются (т.к. рента постнумерандо). Наращенная к концу срока по каждому взносу сумма составит

, , …,,.

Переписав этот ряд в обратном порядке, нетрудно убедиться в том. Что он представляет собой геометрическую прогрессию со знаменателем и первым членом. Число членов прогрессии равно. Искомая величина равна сумме членов этой прогрессии. Откуда

Обозначим множитель, на который умножается , через. Нижний индексуказывает на продолжительность ренты и величину процентной ставки. Будем называть этот множителькоэффициентом наращения ренты. Данный коэффициент представляет собой наращенную сумму ренты, член которой равен 1

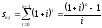
Таким образом

Как было сказано выше, современная стоимость потока платежей – это сумма дисконтированных членов этого потока на некоторый предшествующий момент времени. Вместо термина «современная стоимость» потока платежей в зависимости от контекста употребляют термины капитализированная стоимость или приведенная величина.

Пусть имеется годовая рента постнумерандо, член которой равен , срок ренты -, ежегодное дисконтирование. В этих условиях дисконтированная величина первого платежа равна, второго -, последнего -. Т.е. данные величины образуют ряд, соответствующий геометрической прогрессии с первым членом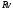и знаменателем. Обозначим сумму членов этой прогрессии через А

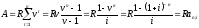
Множитель, на который умножается , называетсякоэффициентом приведения (коэффициентом дисконтирования) ренты, он обозначен как . Этот коэффициент характеризует современную стоимость ренты с членом, равным 1.

При увеличении срока ренты величина стремится к некоторому пределу. Припредельное значение коэффициента составит

Полученное выражение применяется при расчете современной стоимости вечной ренты.

1.7. Планирование погашения долгосрочной задолженности Расходы по обслуживанию долга

Важной целью количественного анализа долгосрочной задолженности является разработка плана погашения займа, адекватного условиям финансового соглашения.

Разработка плана погашения займа заключается в составлении графика периодических платежей должника. Такие расходы должника обычно называют расходами по обслуживанию долга, а также срочными уплатами, расходами по займу. Расходы по обслуживанию долга включают как текущие процентные платежи, так и средства, предназначенные для погашения основного долга.

Методы определения размера срочных уплат существенно зависят от условий погашения долга, которые предусматривают срок займа, продолжительность льготного периода, уровень и вид процентной ставки, методы уплаты процентов и способы погашения основной суммы долга. В льготном периоде основной долг не погашается, обычно выплачиваются проценты. Не исключается возможность присоединения процентов к сумме основного долга.

При определении размера срочных уплат используем следующие обозначения:

D – Сумма задолженности,

Y – срочная уплата,

I – проценты по займу,

R – расходы по погашению основного долга,

g – ставка процентов по займу,

n – общий срок займа.

По определению расходы по обслуживанию долга находятся по формуле