
- •Конспект лекций
- •1. Основы финансовых вычислений
- •1.1. Наращение и дисконтирование Учет фактора времени в финансовом анализе
- •Наращение
- •Дисконтирование
- •1.2. Номинальная и эффективная ставки
- •1.3. Эквивалентные процентные ставки
- •1.4. Финансовая эквивалентность обязательств
- •1.5. Учет инфляции
- •1.6. Постоянные финансовые ренты Виды потоков платежей и их основные параметры
- •Наращенная сумма и современная стоимость постоянной ренты постнумерандо (на примере годовой ренты)
- •1.7. Планирование погашения долгосрочной задолженности Расходы по обслуживанию долга
- •Создание погасительного фонда
- •Погашение долга в рассрочку
- •1.8. Оценка финансовой эффективности производственных инвестиций Характеристика эффективности производственных инвестиций
- •Чистый приведенный доход
- •Внутренняя норма доходности
- •Срок окупаемости
- •Индекс доходности
- •2. Математические основы финансового анализа в условиях риска и неопределенности
- •2.1. Риски и их измерители
- •2.2. Функция полезности дохода
- •2.3. Снижение риска
- •2.4. Виды ценных бумаг. Доходность ценных бумаг
1.2. Номинальная и эффективная ставки
В современных условиях проценты капитализируются, как правило, не один, а несколько раз в году – по полугодиям, кварталам и т.д. Некоторые зарубежные коммерческие банки практикуют даже ежедневное начисление процентов. При начислении процентов несколько раз в году можно воспользоваться формулой сложных процентов

Параметр n
в этих условиях будет означать число
периодов начисления, а под ставкой i
следует понимать ставку за соответствующий
период. Например, при поквартальном
начислении процентов за 5 лет общее
число периодов начисления составит
5×4=20. Множитель наращения по квартальной
(сложной) ставке 8% равен в этом случае
 .
На практике, как правило, в контрактах
обычно фиксируется не ставка за период
начисления, а годовая ставка, и одновременно
указывается период начисления процентов.
Например, «18% годовых с поквартальным
начислении процентов».
.
На практике, как правило, в контрактах
обычно фиксируется не ставка за период
начисления, а годовая ставка, и одновременно
указывается период начисления процентов.
Например, «18% годовых с поквартальным
начислении процентов».
Пусть годовая ставка равна j, число периодов начисления в году – m. Т.о. каждый раз проценты начисляются по ставке j/m. Ставку j называют номинальной. Формулу приращения теперь можно представить следующим образом:
 или
или
 ,
(7)
,
(7)
где N – общее количество периодов начисления.
Чем чаще начисляются проценты, тем быстрее идет процесс наращения.
Введем теперь новое понятие – действительная или эффективная процентная ставка. Эта ставка измеряет тот реальный относительный доход, который получают в целом за год. Т.о. эффективная ставка – это годовая ставка сложных процентов, которая дает тот же результат, что и m-разовое начисление процентов по ставке j/m.
Обозначим эффективную ставку через i. По определению множители наращения по двум ставкам (эффективной и номинальной при m-разовом начислении) должны быть равны друг другу
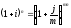 .
.
Из равенства множителей наращения следует
 (8)
(8)
Эффективная ставка
при
 больше номинальной. Замена в договоре
номинальной ставкиj
при m-разовом
начислении процентов на эффективную
ставку i
не изменяет финансовых обязательств
участвующих сторон. Обе
ставки эквивалентны в финансовом
отношении.
Отсюда следует, что разные по величине
номинальные ставки оказываются
эквивалентными, если соответствующие
им эффективные ставки имеют одну
величину.
больше номинальной. Замена в договоре
номинальной ставкиj
при m-разовом
начислении процентов на эффективную
ставку i
не изменяет финансовых обязательств
участвующих сторон. Обе
ставки эквивалентны в финансовом
отношении.
Отсюда следует, что разные по величине
номинальные ставки оказываются
эквивалентными, если соответствующие
им эффективные ставки имеют одну
величину.
По аналогии с
наращением, дисконтирование может
производиться не один, а m
раз в году, т.е. каждый раз учет производится
по ставке f/m.
В этом случае
 ,
(9)
,
(9)
где f – номинальная учетная ставка.
Эффективная
учетная ставка
(d)
характеризует степень дисконтирования
за год. Определим ее на основе равенства
дисконтных множителей
 ,
,
откуда
 .
.
Эффективная учетная ставка во всех случаях, когда m >1, меньше номинальной.
1.3. Эквивалентные процентные ставки
Как было показано выше, разные по величине процентные ставки могут приводить к одинаковым финансовым результатам. Т.е. замена одного вида ставки на другой при соблюдении принципа эквивалентности не изменяет финансовых последствий в рамках одной операции. Для участвующих в сделке сторон в общем безразлично, какой вид ставки фигурирует в контракте. Такие ставки называются эквивалентными.
Эквивалентные ставки – ставки разного вида, применение которых приводит к одинаковому финансовому результату.
Уравнения эквивалентности ставок можно получить исходя из равенства взятых попарно множителей наращения.
Например, определим уравнение эквивалентности между простой и сложной ставками. Для этого прировняем друг к другу соответствующие множители наращения
 ,
,
где
 и
и - ставки простых и сложных процентов.
- ставки простых и сложных процентов.
Приведенное равенство предполагает, что начальные и наращенные суммы при применении двух видов ставок идентичны. Решение приведенного выше равенства дает следующие соотношения эквивалентности
 ,
,

Аналогичным образом определим и другие соотношения эквивалентности ставок.
Эквивалентность простых ставок.
Из равенства соответствующих множителей наращения следует
 ,
,
 ,
,
где n
– срок в годах,
 -
ставка простых процентов,
-
ставка простых процентов, - простая учетная ставка.
- простая учетная ставка.
Эквивалентность простых и сложных ставок
Эквивалентность
 и
и
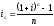 ,
,

Эквивалентность
 и
и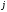
 ,
,

Эквивалентность
 и
и
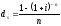 ,
,

Эквивалентность
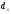 и
и


Эквивалентность сложных ставок
Остановимся только на соотношениях эквивалентности для ставок i, j и d
Эквивалентность
 и
и
 ,
,

Эквивалентность
 и
и
 ,
,

