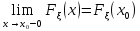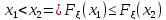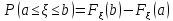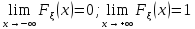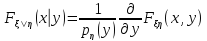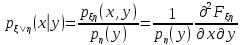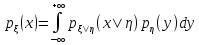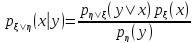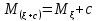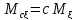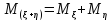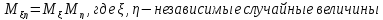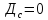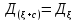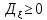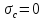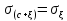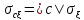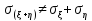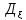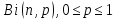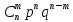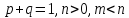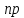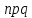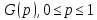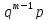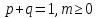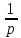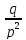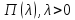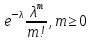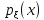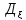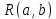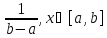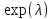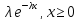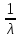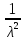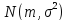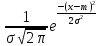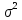ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ ТЕОРИИ ВЕРОЯТНОСТИ

ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ ТЕОРИИ ВЕРОЯТНОСТИ

Вероятность – числовая функция P, определенная на измеримом пространстве (Ω, U):

1. P(A) ≥ 0,

2. 

3. 

4. ;

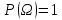
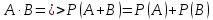
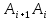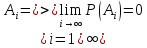
Свойства вероятности:

1. P() = 0

2. 

3. 

4. 

5. 

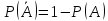
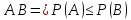
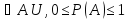
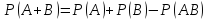
Случайная величина – вещественная функция, заданная на измеримом пространстве (Ω, U) такая, что .

Функция распределения:

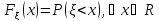
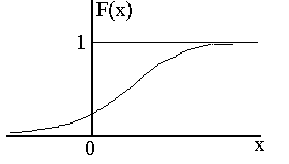
Свойства функции распределения:

1. 

2. 

3. 

4. 

Плотность распределения:

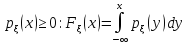
Свойства плотности распределения:

1. 

2. 

3. 

4. 

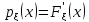
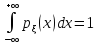
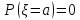5. для непрерывной случайной величины

Совместная функция распределения:

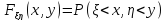
Свойства совместной функции распределения:

1. 

2. 

3. 

4. ,

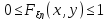
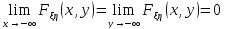
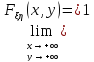
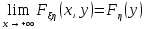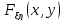5. - функция монотонно не убывает и непрерывна слева по каждой из переменных.

Совместная плотность распределения:

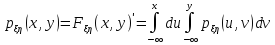
Свойства совместной плотности распределения:

1. 

2. 

3. 

4. ;

5. 

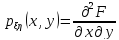
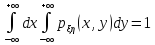
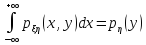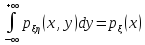
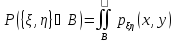
Независимость случайных величин:

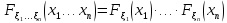
Теорема 1 (дискретная случайная величина)

Теорема 2 (непрерывная случайная величина)

Условное распределение

Условная плотность распределения

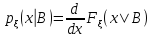
Свойства условного распределения, если B – случайная величина y.

1. 

2. 

3. 

4. 

Функция случайной величины

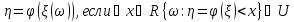
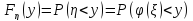
Теорема. Если 𝝽 – непрерывная случайная величина, то

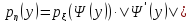, 𝞅(y) – строго монотонная функция, .

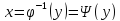Функция от нескольких случайных величин

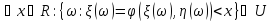
Свертка

Пусть , 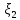– независимые случайные величины, то :

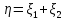Пусть – независимые случайные величины, то

, ,

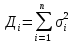
Числовые характеристики

1. Квантиль уровня p:

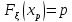
2. Математическое ожидание

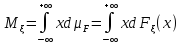
ДСВ: ,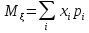

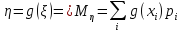
НСВ: ,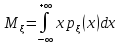

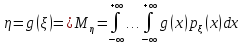
Свойства:

• 

• 

• 

• 

• 

• 

3. Дисперсия

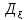
ДСВ:

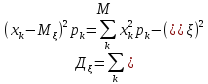
НСВ: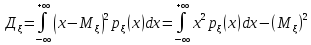

Свойства:

• 

• 

• 

• 

• 

3. Среднее квадратическое отклонение

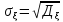
Свойства:

• 

• 

• 

• 

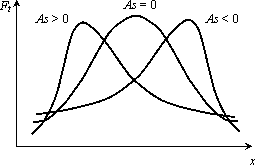
3. Коэффициент асимметрии

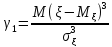
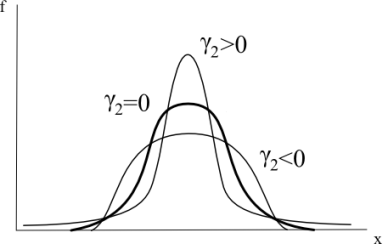
3. Эксцесс

Условные числовые характеристики

ДСВ:

НСВ:

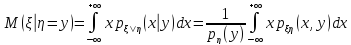
Основные распределения

Распределение
Биноминальное
Геометрическое
Пуассона
Распределение
Равномерное
Экспоненциальное
Нормальное

Числовые характеристики нескольких случайных величин

1. Ковариация

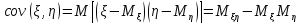
Свойства

• 

• 

• 

• 

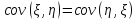
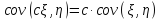
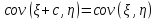
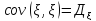
• Если 𝝽, 𝝶 – независимы, тогда

• 

• 

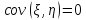
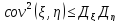
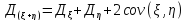
Корреляция

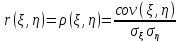
Свойства

• 

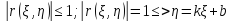
• Если 𝝽, 𝝶 – независимы, тогда

• 

• 

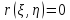
3. Центр рассеивания

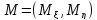
4. Матрица ковариации

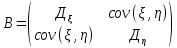
5. Матрица корреляции

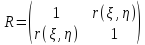
ЗБЧ, ЦПТ, ВБУ

– независимые случайно распределенные случайные величины, где .

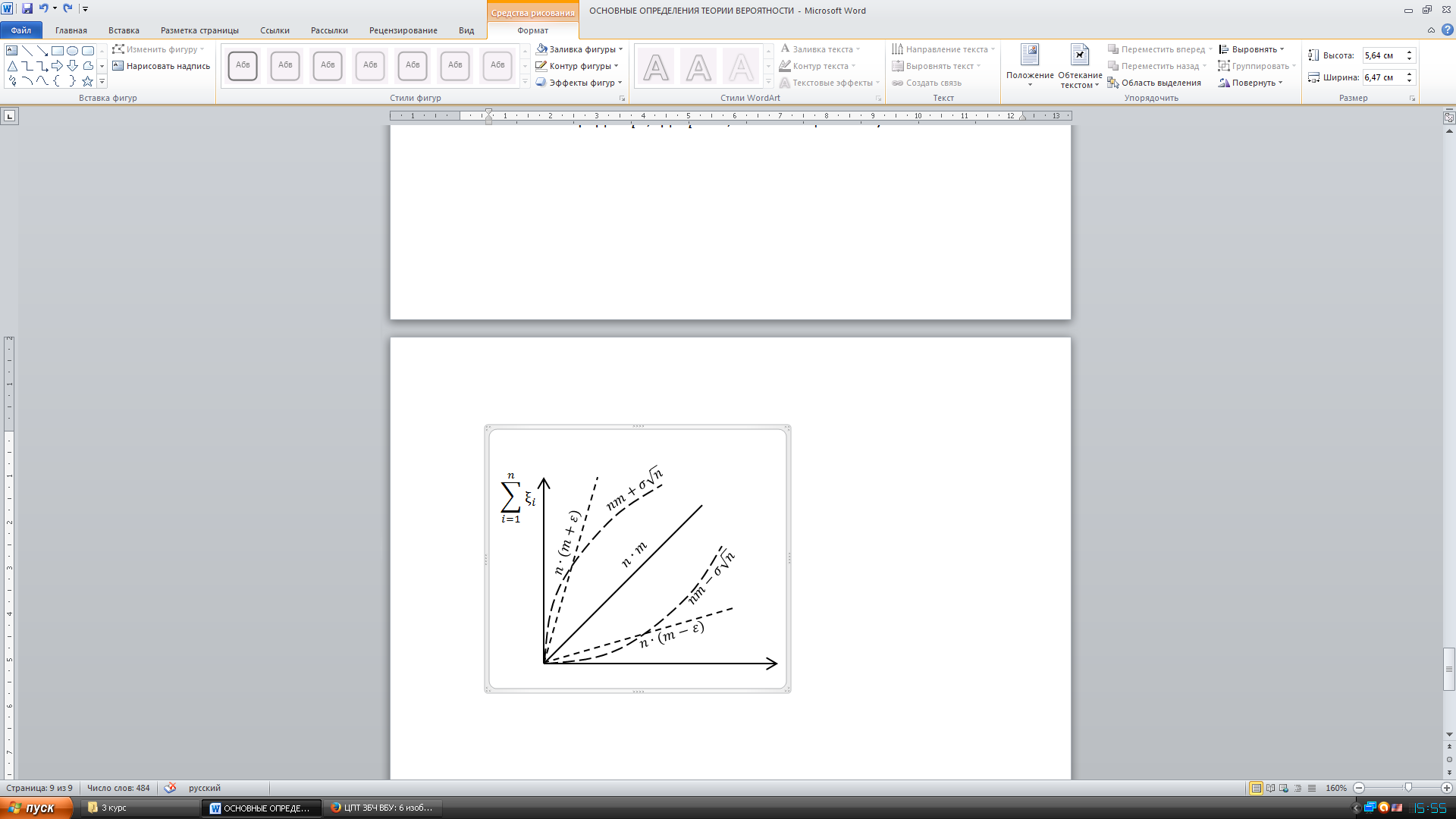
Закон больших чисел. 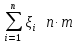, 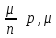– число наступлений события А в серии из n испытаний Бернулли. Типичное поведение суммы имеет порядок n.

Центральная предельная теорема. 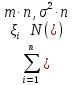. Отклонение от ЗБЧ имеет порядок .

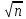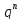Вероятность больших уклонений. имеет порядок , где , экспоненциально убывает.

8