
ЦОС - ЛР2
.docxФедеральное агентство связи
Государственное образовательное учреждение высшего профессионального образования
Московский Технический Университет Связи и Информатики
(МТУСИ)
Кафедра радиотехнических систем
Лабораторная работа №2
Моделирование детерминированных и случайных дискретных сигналов
Выполнила
студентка группы БРА1101
Тюрина А.В.
Проверила
Мирошникова Н.Е.
Москва 2013
ЦЕЛЬ РАБОТЫ
Изучить математическое описание дискретных сигналов и овладеть програмными средствами моделирования в MATLAB.
ИСХОДНЫЕ ДАННЫЕ
|
Переменная |
Назначение |
Значение |
Идентификатор |
|
|
Номер бригады |
Nбр |
Nb = 12 |
|
|
Длина последовательности |
N = 30 + N6ртоd 5 |
N = 32 |
|
|
Период дискретизации |
7 = 0, 0005(1 + Nбр mod13) |
T = 0.0005 |
|
|
Основание экспоненты |
а = (-1) Nбр (0,8 + 0, 005Nбр) |
a = 0.86 |
|
|
Амплитуда гармонического сигнала |
С = 1 + Nбр mod 5 |
C = 3 |
|
|
Частота гармонического сигнала |
|
w0 = pi/8 |
|
|
Задержка |
т = 5 + N бр mod 5 |
m = 7 |
|
|
Амплитуда импульса |
U = N бр |
U = 12 |
|
|
Начальный момент импульса |
n0 =N бр mod 5 + 3 |
n0 = 5 |
|
|
Длина импульса |
nimp = N бр mod 5 + 5 |
n_imp = 7 |
|
|
Амплитуды гармонических сигналов |
B1 = 1,5 + Nбр mod 5 B2= 5,7 - Nбр mod 5 В3 =2,2 + Nбр mod 5 |
Вектор B = [3.5 3.7 4.2] |
|
|
Частоты гармонических сигналов |
|
Вектор w = [pi/6 pi/10 pi/18] |
|
|
Коэффициенты линейной комбинации гармонических сигналов |
α1 =1,5 – Nбр mod 5 α2 = 0,7 + Nбр mod 5 α3=1,4 + Nбр mod 5 |
Вектор A = [-0.5 2.7 3.4] |
|
|
Математическое ожидание |
mean = Nбр mod 5 + 3 |
Mean = 5 |
|
|
Дисперсия |
var= = Nбр mod 5 + 5 |
Var = 7 |
ДОМАШНЕЕ ЗАДАНИЕ
Вариант 12.
1С. Линейная комбинация дискретных гармонических сигналов:
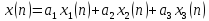 ,
где
,
где

с выводом графиков
последовательностей
 и
и
 на интервале времени
на интервале времени
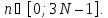
function [ output_args ] = oneC( A,B,w,N )
N=32;
B=[3.5 3.7 4.2];
w=[pi/6 pi/10 pi/18];
A=[-0.5 2.7 3.4];
n=0:(3*N-1);
xi=repmat(B,length(n),1).*real(exp(n'*w));
ai = repmat(A,length(n),1);
x5 = sum((ai.* xi)');
subplot(2,1,2), stem(n,xi), xlabel('n'), ylabel('x'), grid
title('xi')
subplot(2,1,1), stem(n,x5), xlabel('n'), ylabel('x'), grid
title('x5')
end


2С. Дискретный
прямоугольный импульс с амплитудой
 ,
длительностью
,
длительностью
 и моментом начала
и моментом начала
 с выводом графика на интервале времени.
Определить энергию и мощность импульса.
с выводом графика на интервале времени.
Определить энергию и мощность импульса.
function [ output_args ] = twoC( input_args )
N=32;
n0=5;
n_imp=7;
U=12;
n=0:(N-1);
u1 = [1 ones(1,(N-1))]; % ЦИФРОВОЙ ЕДИНИЧНЫЙ СКАЧОК
x3_1 = U*rectpuls(n-n0,2*n_imp); x3_1(1:n0) = 0; % ФОРМИРОВАНИЕ ИМПУЛЬСА С ПОМОЩЬЮ ФУНКЦИИ rectpuls
subplot(1,1,1),stem(n,x3_1,'Linewidth',2), grid
E=sum(x3_1.^2);
P=sum(x3_1.^2)/length(x3_1);
disp([' E = ' num2str(E) ' P = ' num2str(P)])
end
Энергия и мощность импульса:


ЗС. Периодическая
последовательность дискретных
прямоугольных импульсов с амплитудой
 ,
длительностью
,
длительностью
 и периодом, втрое большим длительности
импульса, с выводом графика для заданного
числа периодов.
и периодом, втрое большим длительности
импульса, с выводом графика для заданного
числа периодов.
function [ output_args ] = threeC( input_args )
N=32;
U=12;
n_imp=7;
u1 = [1 ones(1,(N-1))]; % ЦИФРОВОЙ ЕДИНИЧНЫЙ СКАЧОК
xp = [U.*u1(1:n_imp) zeros(1,3*n_imp)]; % ПЕРИОД ПОСЛЕДОВАТЕЛЬНОСТИ
p = 5; % ЧИСЛО ПЕРИОДОВ
x3 = repmat(xp,1,p); % ПЕРИОДИЧЕСКАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ
n = 0:(length(x3)-1); % ДИСКРЕТНОЕ НОРМИРОВАННОЕ ВРЕМЯ
subplot(1,1,1), stem(n,x3,'Linewidth',2), xlabel('n'), grid
end

4С. Оценка
автоковариационной функции
 аддитивной смеси дискретного гармонического
сигнала
аддитивной смеси дискретного гармонического
сигнала
 с нормальным белым шумом с параметрами,
заданными по умолчанию, с выводом графика
оценки автоковариационной функции,
центрированной относительно
с нормальным белым шумом с параметрами,
заданными по умолчанию, с выводом графика
оценки автоковариационной функции,
центрированной относительно
 .
.
function [ output_args ] = fourC( input_args )
N=32;
C=3;
w0=pi/8;
n = 0:(N-1);
x = C.*sin(w0.*n);
x5 = x+randn(1,N);
R = (1/N).*xcorr(x5); % ОЦЕНКА АКФ
m = -(N-1):(N-1); % ВЕКТОР ДИСКРЕТНЫХ СДВИГОВ ДЛЯ АКФ
subplot(1,1,1),stem((m),R,'Linewidth',2),xlabel('m'), grid
title('ACF R(m)')
end

5С. Аддитивная
смесь дискретного гармонического
сигнала
 с нормальным белым шумом с выводом
графика на интервале времени.
с нормальным белым шумом с выводом
графика на интервале времени.
function [ output_args ] = fiveC( input_args )
N=32;
C=3;
w0=pi/8;
n = 0:(N-1); % ДИСКРЕТНОЕ НОРМИРОВАННОЕ ВРЕМЯ
x = C.*sin(w0.*n); % ДИСКРЕТНЫЙ ГАРМОНИЧЕСКИЙ СИГНАЛ
x8 = x+randn(1,N); % АДДИТИВНАЯ СМЕСЬ СИГНАЛА С ШУМОМ
subplot(1,1,1),stem(n,x8,'Linewidth',2),xlabel('n'), grid
end

6С. Оценка АКФ
нормального белого шума с математическим
ожиданием
 и дисперсией
и дисперсией
 с выводом графика оценки АКФ, центрированной
относительно
с выводом графика оценки АКФ, центрированной
относительно
 .
.
function [ output_args ] = six6( input_args )
Mean=5;
Var=7;
r_norm = sqrt(Var).*randn(1,10000)+ Mean; % НОРМАЛЬНЫЙ БЕЛЫЙ ШУМ С ЗАДАННЫМИ МАТ. ОЖИДАНИЕМ И ДИСПЕРСИЕЙ
R_r_norm = (1/length(r_norm)).*xcorr(r_norm); % ОЦЕНКА АКФ
m = -(length(r_norm)-1):(length(r_norm)-1); % ВЕКТОР ДИСКРЕТНЫХ СДВИГОВ ДЛЯ АКФ
subplot(1,1,1),plot(m,R_r_norm,'Linewidth',2), xlabel('m'), grid
end

7С. Дискретный гармонический сигнал с изменением мгновенной частоты (ЧМ-сигнал):

Вычислить с помощью функции:

где
 — векторы значений дискретного времени
— векторы значений дискретного времени
 (с) и последовательности
(с) и последовательности
 ;
;
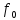 — начальная частота
— начальная частота
 (Гц);
(Гц);
 — момент дискретного
времени
— момент дискретного
времени
 (с) и значение частоты
(с) и значение частоты
 (Гц);
(Гц);
 — закон изменения
мгновенной частоты
— закон изменения
мгновенной частоты
' linear ' — линейный:

' quadratic ' — квадратичный:

' logarithmic ' — логарифмический (в действительности экспоненциальный):

Вывести графики
последовательности
 с помощью функции
с помощью функции
 на интервале дискретного времени
на интервале дискретного времени
 с шагом
с шагом
 при
при
 и различных значениях параметра
и различных значениях параметра
 .
.
function [ output_args ] = sevenC( input_args )
N = 32;
T = 0.0005;
f0 = 10;
f1 = 50;
t1 = 50;
t = 0:T:(50*(N-1)*T);
x = chirp(t,f0,t1,f1,'linear');
subplot(3,1,1), plot(t,x)
title('Linear')
x = chirp(t,f0,t1,f1,'quadratic');
subplot(3,1,2), plot(t,x)
title('Quadratic')
x = chirp(t,f0,t1,f1,'logarithmic');
subplot(3,1,3), plot(t,x)
title('Logarithmic')
end

8С. Последовательность с однотональной амплитудной модуляцией (АМ-сигнал):
 где
где
 — соответственно амплитуда, частота и
начальная фаза несущего колебания;
— соответственно амплитуда, частота и
начальная фаза несущего колебания;
 — частота и начальная
фаза модулирующего колебания;
— частота и начальная
фаза модулирующего колебания;
 — коэффициент
модуляции (глубина модуляции),
— коэффициент
модуляции (глубина модуляции),
 .
.
Вывести графики
последовательности
 с помощью функции
с помощью функции
 на интервале
на интервале
 при следующих значениях параметров
АМ-сигнала:
при следующих значениях параметров
АМ-сигнала:


function [ output_args ] = eightC( input_args )
N=32;
w0=pi/8;
C=3;
phi_0=pi/3;
W=w0/4;
phi_w=pi/6;
m=0.5;
n = 0:(20*N-1);
X = cos(w0*n+phi_0).*(1+m*cos(W*n+phi_w)).*C;
subplot(4,1,1), plot(n, X)
title(strcat([' phi_0 = ',num2str(mean(phi_0)),' W = ',num2str(var(W)),' phi_w = ',num2str(var(phi_w)),' m = ',num2str(var(m))]))
phi_0=0;
phi_w=0;
subplot(4,1,2), plot(n, X)
title(strcat([' phi_0 = ',num2str(mean(phi_0)),' W = ',num2str(var(W)),' phi_w = ',num2str(var(phi_w)),' m = ',num2str(var(m))]))
m=0;
X = cos(w0*n+phi_0).*(1+m*cos(W*n+phi_w)).*C;
subplot(4,1,3), plot(n, X)
title(strcat([' phi_0 = ',num2str(mean(phi_0)),' W = ',num2str(var(W)),' phi_w = ',num2str(var(phi_w)),' m = ',num2str(var(m))]))
m=1;
X = cos(w0*n+phi_0).*(1+m*cos(W*n+phi_w)).*C;
subplot(4,1,4), plot(n, X)
title(strcat([' phi_0 = ',num2str(mean(phi_0)),' W = ',num2str(var(W)),' phi_w = ',num2str(var(phi_w)),' m = ',num2str(var(m))]))
end

9С. Последовательность в виде Гауссова радиоимпульса:

где
 — параметр, управляющий длительностью
радиоимпульса,
— параметр, управляющий длительностью
радиоимпульса,
 — несущая частота.
— несущая частота.
Вывести графики
последовательности
 с помощью функции
с помощью функции
 при следующих значениях параметров
Гауссова радиоимпульса:
при следующих значениях параметров
Гауссова радиоимпульса:

на интервале
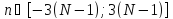 и на интервале
и на интервале
 (со сдвигом в область положительного
времени).
(со сдвигом в область положительного
времени).
function [ output_args ] = nineC( input_args )
N = 32;
w0 = pi/8;
w1 = w0/2;
a = 0;
n = (-3*(N-1)):(3*(N-1));
X = exp(-a*n).*cos(w1*n);
subplot(4,2,1), plot(n, X)
title(strcat(['a = ',num2str(mean(a))]))
a = 0.0005;
X = exp(-a*n).*cos(w1*n);
subplot(4,2,3), plot(n, X)
title(strcat(['a = ',num2str(mean(a))]))
a = 0.001;
X = exp(-a*n).*cos(w1*n);
subplot(4,2,5), plot(n, X)
title(strcat(['a = ',num2str(mean(a))]))
a = 0.005;
X = exp(-a*n).*cos(w1*n);
subplot(4,2,7), plot(n, X)
title(strcat(['a = ',num2str(mean(a))]))
a = 0;
n = 0:(6*(N-1));
X = exp(-a*n).*cos(w1*n);
subplot(4,2,2), plot(n, X)
title(strcat(['a = ',num2str(mean(a))]))
a = 0.0005;
X = exp(-a*n).*cos(w1*n);
subplot(4,2,4), plot(n, X)
title(strcat(['a = ',num2str(mean(a))]))
a = 0.001;
X = exp(-a*n).*cos(w1*n);
subplot(4,2,6), plot(n, X)
title(strcat(['a = ',num2str(mean(a))]))
a = 0.005;
X = exp(-a*n).*cos(w1*n);
subplot(4,2,8), plot(n, X)
title(strcat(['a = ',num2str(mean(a))]))
end
На
интервале
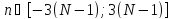 :
:

На
интервале
 :
:

10С. Последовательность

Вычислить с помощью функции:

где
 — векторы значений дискретного времени
— векторы значений дискретного времени
 (с) и последовательности
(с) и последовательности
 .
.
Вывести графики
последовательности
 на интервале
на интервале
 с шагом
с шагом
 и на интервале
и на интервале
 (со сдвигом в область положительного
времени).
(со сдвигом в область положительного
времени).
function [ output_args ] = tenC( input_args )
T = 0.0005;
N = 32;
n = (-500*(N-1)*T):T:(500*(N-1)*T);
x = sinc(n*T);
subplot(2,1,1), plot(n*T,x)
n = 0:T:(1000*(N-1)*T);
x = sinc(n*T);
subplot(2,1,2), plot(n*T,x)
end
На интервале
 :
:

На
интервале
 :
:

ВЫПОЛНЕНИЕ РАБОТЫ
Вариант 12.
1.
Цифровой
единичный импульс
 :
:

График
на интервале дискретного
времени
 :
:

График
на интервале дискретного
нормированного
времени
 :
:

2.
Цифровой
единичный скачок
 :
:

График
на интервале дискретного
времени
 :
:

График
на интервале дискретного
нормированного
времени
 :
:

3.
Дискретная
экспонента
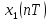 :
:

График
на интервале дискретного
времени
 :
:

График
на интервале дискретного
нормированного
времени
 :
:

4.
Дискретный комплексный гармонический
сигнал
 :
:

Графики
вещественной и мнимой частей на интервале
времени
 :
:

5. Задержанные последовательности:
а)
Задержанный цифровой единичный импульс
 ::
::
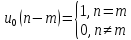

б)
Задержанный цифровой единичный скачок
 :
:


в)
Задержанная дискретная экспонента
 :
:


6.
Дискретный прямоугольный импульс
 :
:

Моделирование импульса с помощью функции rectpuls:

Моделирование импульса на основе цифрового единичного скачка:

7.
Дискретный треугольный импульс
 :
:
Моделирование
импульса посредством
свертки дискретного прямоугольного
импульса
 с
самим собой на интервале времени, равном
длине свертки
с
самим собой на интервале времени, равном
длине свертки
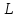 :
:


8.
Линейная комбинация дисретных
гармонических сигналов
 :
:
 ,
где
,
где

Графики
последовательностей
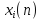 и
и
 на интервале времени
на интервале времени
 :
:

9. Дискретный гармонический сигнал с экспоненциальной огибающей.
График
дискретного гармонического сигнала
 ,
представляющий собой дискретный
гармонический сигнал
,
представляющий собой дискретный
гармонический сигнал
 с экпоненциальной огибающей
с экпоненциальной огибающей
 на интервале времени:
на интервале времени:

10. Периодическая последовательность дискретных прямоугольных импульсов.
График
пяти периодов периодической
последовательности
 ,
дискретных
прямоугольных импульсов амплитуды
,
дискретных
прямоугольных импульсов амплитуды
 и
длительности
и
длительности
 с
периодом, вдвое большим длительности
импульса:
с
периодом, вдвое большим длительности
импульса:

11. Равномерный белый шум.
Математическое ожидание и дисперсия:
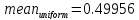

График
оценки автоковариационной функции
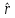 x(т)
шума,
центрированной относительно т
=
0 .
x(т)
шума,
центрированной относительно т
=
0 .

12. Нормальный белый шум.
Математическое ожидание и дисперсия%

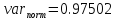
График
оценки АКФ
 x(т)
шума,
центрированной
относительно т
= 0
.
x(т)
шума,
центрированной
относительно т
= 0
.

13. Аддитивная смесь х8(п) дискретного гармонического сигнала х(п) с нормальным белым шумом с выводом графика на интервале времени.

14.
Оценка
АКФ
 x(т)
последовательности х8(п).
График
АКФ, центрированной относительно т
= 0.
x(т)
последовательности х8(п).
График
АКФ, центрированной относительно т
= 0.

Оценка дисперсии последовательности х8(п) и значение Rx (N).


15. Нормальный белый шум с заданными статистическими характеристиками.
Графики четырех разновидностей нормального белого шума длины 10 000:
-
с математическим ожиданием и дисперсией, установленными по умолчанию;
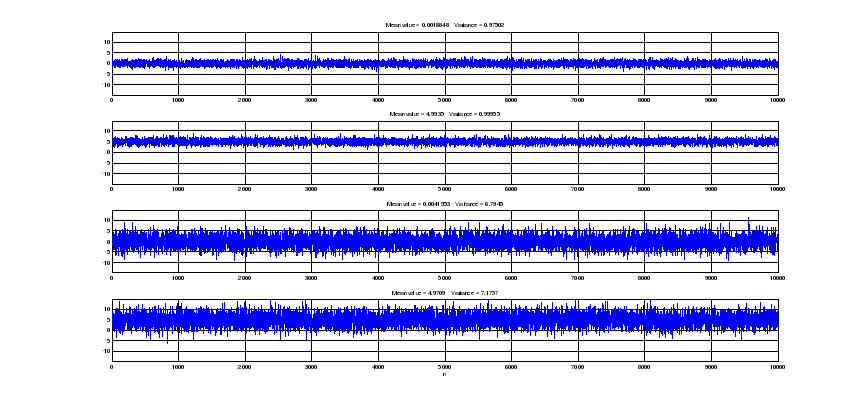
-
с математическим ожиданием mean и дисперсией, установленной по умолчанию;

-
с математическим ожиданием, установленным по умолчанию, и дисперсией Var;

-
с математическим ожиданием mеаn и дисперсией vаг.

Гистограммы четырех разновидностей нормального белого шума I с помощью функции hist.







 ,
рад
,
рад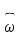 o
= π/(6 + N
бр
mod
5)
o
= π/(6 + N
бр
mod
5)





 =
π/(4
+ Nбр
mod
5)
=
π/(4
+ Nбр
mod
5)
 =
π/(8
+ N,бр
mod
5)
=
π/(8
+ N,бр
mod
5) =
π/(16
+ Nбр
mod
5)
=
π/(16
+ Nбр
mod
5)

