-2: к.т.н., доц. Корзинкин Владимир Анатольевич;

-1: Общая теория связи

4. Обобщенная структурная схема телекоммуникационной системы передачи информации (ТКС). Назначение элементов.

Источник сообщения – это некоторый объект или система, информацию о состояние которой необходимо передать

ФНЧ – ограничивает спектр сигнала на верхней частоте F_B

Дискретизатор – представляет отклик ФНЧ в виде последовательности отсчетов х_k

Квантователь – преобразует отсчеты в квантовые уровни x_k⁽ⁿ⁾ ; k = 0, 1, 2… ;

, где L- число уровней квантования.

Кодер – кодирует квантованные уровни двоичным безызбыточным кодом, т.е. формирует последовательность комбинаций ИКМ b_k⁽ⁿ⁾.

Модулятор – формирует сигнал, амплитуда, частота или фаза которого изменяются в соответствии с сигналом b_k⁽ⁿ⁾.

Выходное устройство ПДУ – осуществляет фильтрацию и усиление модулированного сигнала для предотвращения внеполосных излучений и обеспечения требуемого соотношения сигнал/шум на входе приемника. Линия связи – среда или технические сооружения по которым сигнал поступает от передатчика к приемнику. В линии связи на сигнал накладывается помеха.

Входное устройство ПРУ – осуществляет фильтрацию принятой смеси – сигнала и помехи.

Детектор – преобразует принятый сигнал в сигнал ИКМ .

Декодер – преобразует кодовые комбинации в импульсы

Интерполятор и ФНЧ восстанавливают непрерывный сигнал из импульсов – отсчетов.

Получатель – некоторый объект или система, которому передается информация.

5. АЦП(вариант \4\):

Аналого-цифровое преобразование(АЦП) осуществляется в три этапа. Вначале сообщение дискретизируется по времени, далее квантуется по уровню и затем квантованные уровни кодируются. В результате чего формируется сигнал импульсно-кодовой модуляции(ИКМ).

Теоретической основой дискретизации служит теорема Котельникова. Суть её в следующем: любая непрерывная функция x(t), ограниченная по спектру верхней частотой Fв, может быть точно представлена последовательностью своих отсчётов 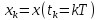, взятых в моменты времени, кратные интервалу дискретизации 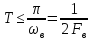. Откликx(t) идеального ФНЧ удовлетворяет этой теореме. Поэтому его можно продискретизировать, т.е. преобразовать из аналоговой формы x(t) в дискретно-аналоговую {}, с частотой дискретизации.

Дискретизатор можно реализовать в виде перемножителя двух функций: непрерывного сообщения x(t) и периодической последовательности дискретизирующих импульсов .

Рис 2а

Отклик дискретизатора (заштрихованная последовательность импульсов)

Рис 2б

В момент импульсы на выходе дискретизатора могут принимать бесчисленное множество значений из ограниченного или неограниченного диапазона, называемого шкалой сообщения. В результате равномерного квантования с шагомэтот диапазон разбивается на конечное число уровней квантования. На рисунке 2б и 2в показана процедура квантования дляL=4. На экзамене нужно нарисовать для L=8!

Рис2в.

Шаг квантования можно рассчитать следующим образом:

Пороги квантования:

Уровни квантования:

Характеристика квантователя для L=8:

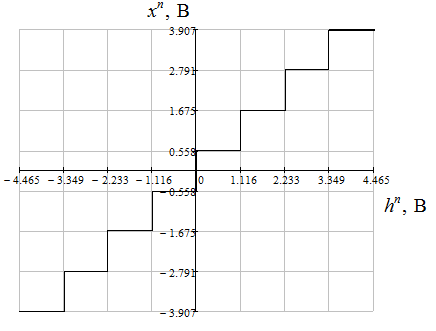
6. ЦАП(вариант \4\):

Цифро-аналоговое преобразование(ЦАП) позволяет на приёмном конце системы связи восстановить непрерывное сообщение по принятым двоичным комбинациям сигнала ИКМ. Это осуществляется с помощью следующих процедур:

а) детектирование – восстановления дискретных L-ичных уровней по

б) интерполяции

в) низкочастотной фильтрации

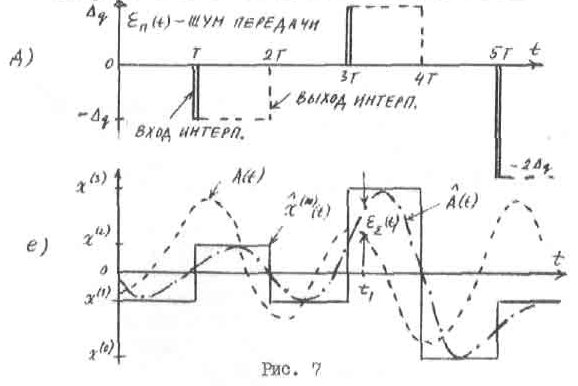
7. Сигналы, спектры на входе и выходе дискретизатора:

8. Сигналы на входе и выходе квантователя:

Сигнал на входе квантователя:

Сигнал на выходе квантователя:

9. Сигналы на входе и выходе восстанавливающего устройства:

10. Модель аналогового ам сигнала:

Амплиту́дная модуляция — вид модуляции, при которой изменяемым параметром несущего сигнала является его амплитуда

При АМ амплитуда несущего ВЧ колебания изменяется в соответствии с модулирующим НЧ сигналом.

(7.1)

Um - средняя амплитуда АМ сигнала.

- глубина (коэффициент) АМ.

Если модулирующий сигнал гармонический:

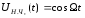
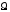- модулирующая, низкая частота,

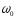- несущая, высокая частота, то АМ сигнал принимает вид:

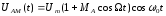(7.2)

Временная диаграмма НЧ сигнала:

Uнч(t)

Рис.7.1

t

Временная диаграмма модулированного сигнала ам:

u_АМ(t)

U

Um t

Рис.7.2

В соответствии с временной диаграммой глубина амплитудной модуляции равна:

М_A=U/Um. (7.3) . Определим спектр АМ сигнала, для чего раскроем скобки в выражении для АМ и представим произведение косинусов в виде косинуса суммы и разности углов:

(7.4)

Спектр модулирующего сигнала .

U

Рис.7.3

 

Спектр АМ сигнала.

u U_m несущая

нижняя M_AU_m M_AU_m верхняя

боковая 2 2 боковая

₀- ₀ ₀+

Рис.7.4

- ширина спектра сигнала АМ – полоса частот, в пределах которой заключена основная доля энергии сигнала.

(7.5)

Боковые имеют высоту (амплитуду) не более половины несущей.

11. Модель аналогового чм сигнала:

Частотная модуляция (ЧМ) — вид аналоговой модуляции, при котором информационный сигнал управляет частотой несущего колебания. По сравнению с амплитудной модуляцией здесь амплитуда остаётся постоянной.

а) — несущая частота, б) модулирующий сигнал, в) результат модуляции

При ЧМ частота ВЧ колебания (несущей) изменяется в соответствии с НЧ модулирующим сигналом.

_чм (t) = ₀ + U_нч(t), где (9.1)

_чм (t)- частота ЧМ сигнала;

₀- среднее значение несущей частоты;

U_нч(t)-модулирующий сигнал;

-девиация частоты, т.е. максимальное отклонение частоты от среднего значения.

Если модулирующий сигнал гармонический, т.е.

U_нч = cost,

то _чм(t) = ₀ + соst

а выражение для ЧМ сигнала имеет вид:

_чм(t) =

U_чм(t) = U_mcos(₀t+

M_ч - индекс ЧМ. (9.2)

U_чм(t) = U_mcos(₀t+

Временная диаграмма модулирующего сигнала имеет вид:

Uнч(t)

Рис.9.1.

t

Временная диаграмма соответствующего ЧМ сигнала принимает вид:

Uчм(t)

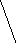
Рис.9.

t

Как видно из рис.9.2, там, где модулирующий сигнал больше, там и частота ЧМ сигнала больше , а период колебаний меньше.

_чм(t) = ₀ + cost

_max = ₀ + 

_min = ₀ - 

Амплитуда при ЧМ постоянна, меняется только частота.

Для получения спектра ЧМ сигнала разложим U_чм(t) в ряд Фурье.

U_чм(t) = U_mcos(₀t+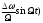= U_m₀(M_ч)cos₀t+ U_m₁(M_ч)cos(₀+)t- U_m₁(M_ч)cos(₀)t+U_m₂(M_ч)cos(₀+2)t+U_m₂(M_ч)cos(₀2)t+U_m₃(M_ч)*cos(₀+3)t- U_m₃(M_ч)cos(₀-3)t+

_k(M_ч) - функция Бесселя к-ого порядка.

Вид спектра зависит от М_ч.

Спектр ЧМ сигнала при М_ч<<1 (т.е. порядка 0,1; 0,05;)

u U_m несущая

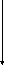
нижняя M_чU_m M_чU_m верхняя

боковая 2 2 боковая

₀- ₀ ₀+

Рис.9.3.

При М_ч<<1 спектр ЧМ сигнала похож на спектр АМ сигнала (несущая, 2 боковых ), но для ЧМ этот спектр приближенный. Все остальные боковые тоже есть, но они очень малы.

Спектр ЧМ сигнала при М_ч>1 выглядит так (Мч=5):

Полоса частот сигнала ЧМ.

П_чм  2(М_ч+1)

М_ч<<1 П_чм  2, ( как при АМ )

М_ч>>1 П_чм  2М_ч = 22

Ширина спектра при Мч>>1 не зависит от модулирующей частоты. Это широкополосный сигнал.

Основные преимущества ЧМ, перед АМ — энергоэффективность и помехоустойчивость.