Федеральное агенство связи

Государственное образовательное учреждение

высшего профессионального образования

МОСКОВСКИЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ СВЯЗИ И ИНФОРМАТИКИ

Кафедра теории электрической связи

Курсовая работа

по дисциплине: «Теория электрической связи»

Факультет: ЗОТФ

Группа: МС 1053

Курс: 4

Шифр: ЗМС 09022

Вариант: 22

Студент: Вадченко О.А.

Москва 2013

Часть 2.1 «разработка кодека»

Задание 1

Нарисовать структурную схему цифровой системы связи и указать назначение основных блоков.

Решение:

Рис.1 Структурная схема цифровой системы связи

ИИ – источник информации;

ФНЧ – фильтр низких частот с верхней частотой пропускания F_в;

АЦП – аналогово-цифровой преобразователь;

БЭК – блок эффективного кодирования;

БПК – блок помехоустойчивого кодирования;

Мод – модулятор несущей;

Вых У – выходное устройство (выходные усилитель и фильтр);

ИП – источник помех ζ(t);

ЛС – линия (канал) связи;

Вх У – входное устройство (входной фильтр и усилитель приемника);

Демод – демодулятор входного сигнала;

БПД – блок помехоустойчивого декодирования;

БЭД – блок эффективного декодирования;

ЦАП – цифро-аналоговый преобразователь;

ПИ – приемник информации.

Задание 2

Записать свои фамилию, имя, отчество и выбрать первые 10 букв. Каждая буква – это импульс-отсчет некоторого процесса. Амплитуда отсчета равна порядковому номеру буквы. Закодировать эти отсчеты двоичным кодом (m=2, n=5), нарисовать эти отсчеты и соответствующий им сигнал ИКМ.

Решение:

Заданная фамилия: ВАДЧЕНКО ОЛЬГА АЛЕКСАНДРОВНА – отсюда 10 букв – ВАДЧЕНКО ОЛ, соответствует некоторому гипотетическому непрерывному сигналу, отсчеты которого в тактовые моменты времени равны: 2в, 0в, 4в, 23в, 5в, 13в, 10в, 14в, 14в, 11в.

Запишем последовательность отсчетов двоичными числами. Для двоичного кода основание m=2, длина кодовой комбинации по заданию равна n=5. Общее количество уровней, которое мы можем закодировать равно N=mⁿ=2⁵=32. Получим кодовые комбинации:

В – 2в – 00010 А– 0в – 00000 Д – 4в – 00100 Ч – 23в – 10111 Е – 5в – 00101 Н – 13в – 01101 К – 10в – 01010 О – 14в –01110 О – 14в –01110

А – 11в – 01011

Квантованный сигнал (импульсы-отсчеты) x_кв (t) и соответствующий ему двоичный сигнал ИКМ x_икм (t) представлены на рисунке 2.

Рис. 2 Квантованный сигнал и соответствующий ему двоичный сигнал ИКМ

Задание 3

­­Рассчитать дисперсию шума квантования, если U_max равна 8 В.

Решение:

Дисперсия шума квантования (формула (3) в методических указаниях):

Шаг квантования :

В итоге дисперсия шума квантования равна:

Задание 4

Определить вероятность дибитов 00, 01, 10, 11 в двоичной последовательности сигнала ИКМ, полученной в задании 2.2. Рассчитать энтропию источника с полученной вероятностью дибитов. Закодировать дибиты двоичным кодом с префиксными свойствами и определить его энтропию, избыточность и среднюю длину кодовой комбинации.

Решение:

4.1. Последовательность двоичных импульсов сигнала ИКМ состоит из «дибитов» («дибит» - это комбинация из 2-х символов: 00, 01, 10, 11). Определяем вероятность каждого «дибита» и кодируем их безызбыточным кодом с префиксными свойствами.

Полученную в задании 2.2 последовательность разделим на «дибиты»:

00 01 00 00 00 00 10 01 01 11 00 10 10 11 01 01 01 00 11 10 01 11 00 10 11

Всего 25 «дибитов». Количество комбинаций:

00 – 8 р(00) = 8/25 = 0,32

01 – 7 р(01) = 7/25 = 0,28

10 – 5 р(10) = 5/25 = 0,20

11 – 5 р(11) = 5/25 = 0,20

4.2. Энтропия – это среднее количество информации, приходящееся на один символ, посылку.

(дв.ед.) – количество информации, содержащееся в символе, если р – вероятность появления этого символа.

Энтропия дискретного источника:

Рассчитаем энтропию в нашем случае:

дв. ед./символ

4.3. Построим код с префиксными свойствами по алгоритму Хаффмана:

1. Располагаем сообщения в порядке убывания вероятностей;

2. Объединяем два наименее вероятных сообщения в одно с суммарной вероятностью появления;

3. Вновь располагаем сообщения в порядке убывания вероятностей и т.д., пока не получим в сумме единицу.

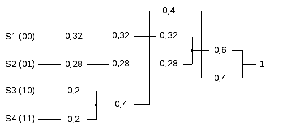
В результате кодирования получим:

S1 (00) – 11

S2 (01) – 10

S3 (10) – 01

S4 (11) – 00

Мы получили код с префиксными свойствами. Исходной ИКМ-последовательности

00 01 00 00 00 00 10 01 01 11 00 10 10 11 01 01 01 00 11 10 01 11 00 10 11

соответствует следующая кодовая последовательность:

11 10 11 11 11 11 01 10 10 00 11 01 01 00 10 10 10 11 00 01 10 00 11 01 00

4.4. Рассчитаем энтропию нового двоичного кода. Для этого надо определить вероятности нулей и единиц в новом коде.

Из 100 среднестатистических сообщений мы имеем сообщений:

S1 – 32 штуки, т.е. 32 комбинации «11»

S2 – 28 штук, т.е. 28 комбинаций «10»

S3 – 20 штук, т.е. 20 комбинаций «01»

S4 – 20 штук, т.е. 20 комбинаций «00»

Таким образом, в 100 сообщениях содержится «единиц»:

N1=32*2+28*1+20*1=64+28+20=112

Содержится «нулей»:

N0=28*1+20*1+20*2=28+20+40=88

Вероятность появления единиц и нулей:

p(1)=N1/(N1+N0)=112/(112+88)=0,56

p(0)=1– p(1)=0,44

Энтропия нового двоичного источника Н:

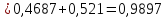дв.ед./символ

4.5. Избыточность нового двоичного источника:

R`` = 1 – 0,9897 = 0,01

4.6. Определим среднюю длину кодовой комбинации:

,

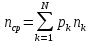где P_k – вероятность k-го сообщения;

n_k – длина кодовой комбинации k-го сообщения.

Следовательно, получим:

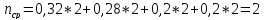двоичных символов.

Задание 5

Осуществить помехоустойчивое кодирование двоичных информационных комбинаций, используя для этого блочный двоичный код.

Необходимо описать алгоритм кодирования и декодирования, записать разрешенные комбинации на выходе кодера для всех возможных информационных комбинаций на входе; зарисовать структурные схемы кодера и декодера.

Решение:

Алгоритм кодирования блочным двоичным кодом

Рассмотрим алгоритм кодирования для двоичного блочного кода (7,3), у которого каждое слово имеет 7 символов, из которых 3 – информационные и 4 – проверочные.

Алгоритм формирования кодовых комбинаций следующий:

1. Присваиваем каждому символу кода номер: а₁, а₂, а₃, а₄, а₅, а₆, а₇.

Первые три символа (а₁, а₂, а₃) являются информационными. Последние четыре символа (а₄, а₅, а₆, а₇) – корректирующие (проверочные).

2. Составляем порождающую матрицу G. Эта матрица должна иметь n столбцов и k строк. Левая часть матрицы – это единичная матрица размером k*k. Правая часть G – это матрица-дополнение Р размером (n-k)*k:

Матрица-дополнение имеет вид:

3. Формируем кодовые комбинации. Для этого сначала записываем все возможные информационные комбинации из трех символов (всего восемь комбинаций): 000, 001, 010, 011, 100, 101, 110, 111.

4. К информационным символам приписываем четыре проверочных символа, получающиеся в результате умножения информационного вектора-строки (а₁ а₂ а₃) на матрицу-дополнение Р. Произведение есть вектор-строка (а₄ а₅ а₆ а₇):

(а₁ а₂ а₃) * Р = (а₄ а₅ а₆ а₇).

Очевидно, для заданной матрицы Р:

;

;

;

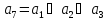
Знак 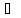означает суммирование по модулю 2, т.е.

, , , .

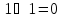Составим кодовую таблицу разрешенных кодовых комбинаций:

	Значения символов комбинации
№	а1	а2	а3	а4	а5	а6	а7
1	0	0	0	0	0	0	0
2	0	0	1	1	1	0	1
3	0	1	0	1	0	1	1
4	0	1	1	0	1	1	0
5	1	0	0	0	1	1	1
6	1	0	1	1	0	1	0
7	1	1	0	1	1	0	0
8	1	1	1	0	0	0	1

Для полученного кода d_min = 4, т.е. наш код может исправлять все одиночные ошибки и некоторые двойные.

Алгоритм декодирования

Принятые кодовые комбинации необходимо сравнить с каждой из разрешенных комбинаций и принять решение о переданном кодовом слове. Однако, количество операций, необходимых для такого алгоритма, быстро растет с ростом n. Более оптимальным способом является вычисление синдрома, т.е. указателя позиции, в которой произошла ошибка.

1. Составляем проверочную матрицу Н:

2. Вычисляем синдром принятой кодовой комбинации, т.е. кодовую комбинацию, равную произведению принятого вектора-строки на транспонированную проверочную матрицу:

;

;

;

,

Где а₁, а₂ … а₇ – принятый кодовый символ, возможно искаженный помехой.

Синдром не зависит от переданной комбинации. Он зависит только от позиции, в которой произошла ошибка.

3. Формируем вектор ошибки V, т.е. кодовую комбинацию, которая содержит единицу той позиции, где произошла ошибка. Формирование синдромов и векторов ошибок можно произвести заранее, искажая последовательно символы и комбинации.

Например, приняли: 0 0 0 0 0 0 0;

(С₁С₂С₃С₄) = 0 0 0 0; V = (0 0 0 0 0 0 0) – ошибок нет.

Пусть приняли: 0 0 0 0 0 0 1 – это запрещенная комбинация (ошибка в символе а₇). Вычисляем синдром: (С₁С₂С₃С₄) = 0001.

Вычисляем вектор ошибки: V = (0 0 0 0 0 0 1)

Составим таблицу синдромов и соответствующих векторов одиночных ошибок О(I):

Вектор ошибки	0000000	0000001	0000010	0000100	0001000	0010000	0100000	1000000
Синдром	0000	0001	0010	0100	1000	1101	1011	0111

Пусть передавали некоторую комбинацию; приняли комбинацию (1110011) – это запрещенная комбинация. Ее синдром: (С₁С₂С₃С₄) = 0010. Из таблицы находим вектор ошибки (0000010), т.е. ошибка произошла в шестом символе. Следовательно, исправив шестой символ ( 1 на 0), получим правильную комбинацию: 1110001.

Рис. 3 Структурная схема кодера

Рис. 4 Структурная схема декодера

Разобьем кодовую последовательность, полученную в п. 2.4, на информационные комбинации по 3 бита и дополним ее произвольными битами (например, 0):

111 011 111 111 011 010 001 101 010 010 101 011 000 110 001 101 00(0)

Закодируем последовательность в соответствии с кодовой таблицей разрешенных кодовых комбинаций:

1110001  0110110  1110001  1110001  0110110  0101011  1011010  0101011  0101011  0101011  1011010  0110110  0000000  1101100  0011101  1011010 0000000