ЦОС, лекция от 14.10.14

Лекция по ЦОС, 14.10.14

Примеры спектров и корреляционных функций некоторых сигналов и СПМ (спектральная плотность мощности)

Пример 1:

Прямоугольный импульс

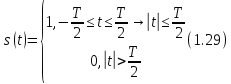
Если взять и подставить интеграл, получим спектр:

Спектральная плотность мощности:

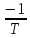
Корреляционная функция:

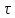
так же можно найти, взяв обратное преобразование Фурье от (теореме Виннера-Хинчица).

Пример 2:

Нецентрированный прямоугольный импульс

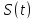
Спектр сигнала:

Т. е., спектральные плотности у совмещенного и нецентрированного сигнала совпадают.

Корреляционная функция:

Основные соотношения связаны парой преобразований Фурье .

Выпишем три основных соотношения для теории непрерывных сигналов, связанные с парой преобразований Фурье:

1. 

(1.37)

2. 

(1.38)

3. 

(1.39)

Определение (скалярного) произведения двух непрерывных сигналов:

Пусть и – два непрерывных, в общем случае, комплексных сигнала с конечной энергий, т. е., энергией , тогда их скалярным произведением называется величина:

В частном случае, когда :

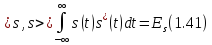
Пусть сигнал – любой непрерывный комплексный сигнал с конечной энергией , тогда:

По смыслу, совпадает со среднеквадратическим значением сигнала.

Пусть сигналы 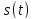и имеют конечную энергию, тогда расстоянием между этими сигналами называется величина:

Из формулы (1.43) следует, что расстояние между двумя сигналами определяется как норма разностного сигнала .

Обобщенное равенство Персенваля:

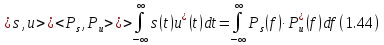
В частном случае, когда , получаем классическое равенство Персенваля:

2. Основные понятия из теории дискретных сигналов

2.1. Дискретизация непрерывных сигналов. Понятия дискретного спектра, дискретной корреляционной функции, дискретной СПМ.

Пусть задан непрерывный, в общем случае, комплексный сигнал с конечной энергией , тогда модель (процедура) дискретизации описывается следующим выражением:

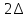
Обоснование модели дискретизации (2.1) основывается на фильтрующем свойстве -функции:

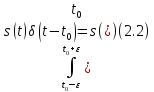
Очевидно, из свойства (2.2) непосредственно следует справедливость модели дискретизации.