Частота дискретизации * число разрядов (n)

Исходя из чего выбирается частота дискретизации?

Выбор частоты дискретизации в общем случае зависит от характеристик сообщения и определяется теоремой Котельникова (теоремой отсчетов):

"Если наивысшая частота в спектре функции S(t) меньше, чем f_m, то функция S(t) полностью определяется последовательностью своих значений в моменты, отстоящие друг от друга не более чем на 1/2f_m секунд".

Чтобы точно отобразить аналоговый сигнал в диапазоне до f _m, отсчеты должны следовать с периодом, по крайней мере, в два раза меньшим, чем период частоты f _m.

Иными словами, частоту дискретизации следует выбирать так, чтобы она была, по меньшей мере, в два раза выше максимальной частоты спектра сигнала.

Реальные сигналы конечной длительности всегда имеют бесконечно широкий спектр, более или менее быстро убывающий с ростом частоты. Поэтому дискретизация сигналов всегда приводит к потерям информации (искажению формы сигнала при дискретизации—восстановлении), как бы ни была высока частота дискретизации.

CD Digital Audio - частота дискретизации равна 44,1 кГц.

DVD-audio, частота дискретизации может быть равной 44,1/48/88.2/96 кГц, разрешающая способность 16/20/24 бит, количество каналов — до 6.

Декодирование (восстановление первичного электрического сигнала)

На приемном конце канала связи имеем последовательность групп двоичных символов (по n символов в каждой группе).

Каждому набору символов соответствует определенное число.

Натуральное число, записываемое в двоичной системе счисления как , имеет значение:

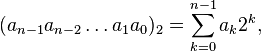
где: — количествоцифр(знаков) в числе,— значение символа {0,1},— порядковый номер символа в кодовой группе (слове).

Для преобразования цифровой последовательности в исходное сообщение используется ЦАП – устройство, которое формирует значение тока или напряжения на выходе соответственно натуральному числу (кодовой комбинации).

ЦАП восстанавливает последовательность отсчетов.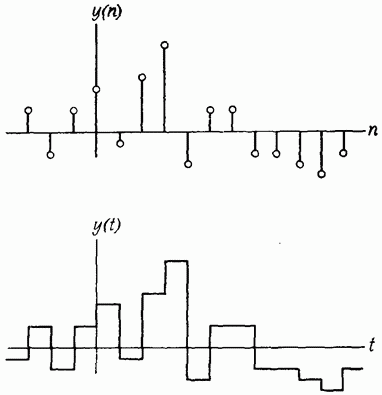

Эти отсчеты подаются на фильтр.

На выходе фильтра получаем приближение исходного сообщения.

Помехоустойчивое кодирование

Когда передается сообщение от источника к приемнику, при передаче данных может произойти ошибка (помехи, неисправность оборудования и пр.).

Пример: 0 0 1 1 1 1 0 0 0 0 11111 000000

0 0 0 1 1 1 0 0 1 0 11111 000000

Чтобы обнаружить и исправить ошибку, применяют помехоустойчивое кодирование, т.е. кодируют сообщение таким образом, чтобы принимающая сторона знала, произошла ошибка или нет, и по возможности могла обнаружить и в лучшем случае исправить ошибки в случае их возникновения.

Помехоустойчивое кодирование — это добавление к исходной информации дополнительной, проверочной, информации.

Для помехоустойчивого кодирования:

• на передающей стороне используются помехоустойчивый кодер,

• на принимающей стороне — декодер.

Прямая теорема Шеннона для канала с шумами

Для канала с помехами всегда можно найти такую систему кодирования, при которой сообщения будут переданы со сколь угодно большой степенью верности, если только производительность источника не превышаетпропускной способности канала.

Обратная теорема Шеннона

Если скорость передачи больше пропускной способности, то есть , то не существует таких способов передачи, при которых вероятность ошибки стремится к нулю () при увеличении длины передаваемого блока, ().

Предел Шеннона

Под пределом (границей) Шеннона понимается максимальная скорость передачи, для которой код имеет возможность исправить ошибки в канале с заданным отношением сигнал/шум.

Известны коды очень большой длительности. Например, максимальное приближение к этой границе даёт LDPC-кодс примерной длиной блока в 10 миллионовбит.

С другой стороны, в качестве границы Шеннона также рассматривают (понимают) минимальное отношение сигнал/шум, для которого теоретически возможно безошибочная передача и декодирование блока с заданной скоростью.

Например, для вида модуляции QPSKи скорости передачи 1 (бит/с)/символ минимальное отношение сигнал/шум составляет 0,25 дБ.

Децибел = 10* Log ₁₀ (Р _{сигнала}/Р _шума)