Примерные вопросы и задачи по курсу ТФКП

Примерные вопросы и задачи по курсу ТФКП

1. Комплексное число, его модуль и аргумент. Запись комплексного числа в алгебраической, тригонометрической и показательной форме. Формула Эйлера.

Задача 1. Записать комплексные числа в указанных видах:

; ; .

Сумма (разность), произведение и частное двух комплексных чисел. Извлечение корня -ной степени из комплексного числа.

Задача 2. Для чисел и вычислить сумму, разность, произведение и частное.

Задача 3. Для чисел и вычислить сумму, разность, произведение и частное.

Задача 4. Решить уравнение и представить ответы в алгебраической, тригонометрической и показательной форме.

2. Построение областей в комплексной плоскости , заданных системой неравенств.

Задача 5. Построить область:

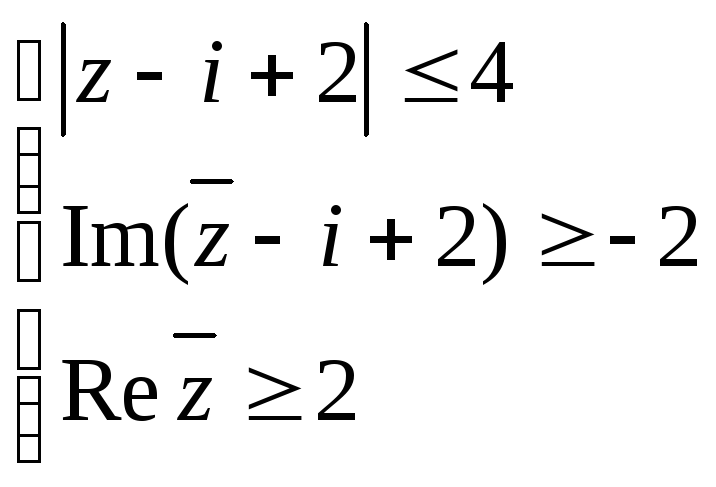
Задача 6. Построить область:

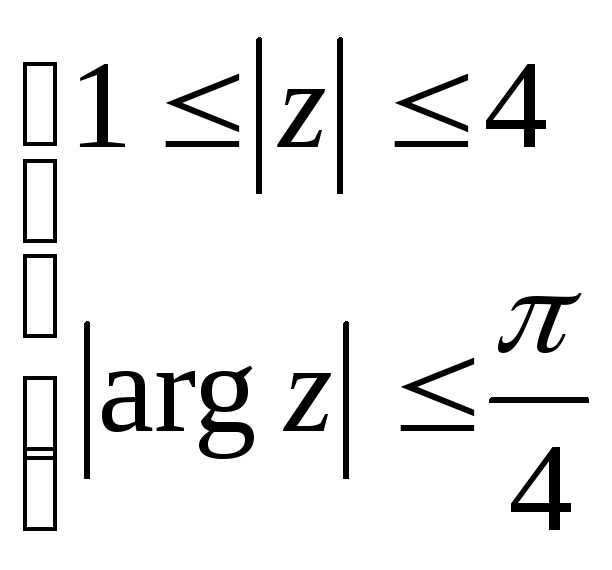
4. Конформные отображения.

Задача 7. В плоскости дано уравнение линии . Ра какую линию она отображается функцией . Привести чертеж.

3. Определение основных функций ТФКП: 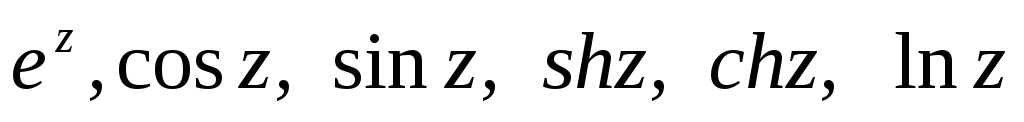. Вычисление значений функций для заданных аргументов.

Задача 7. Вычислить: .

4. Преобразование функций комплексного переменного к виду: 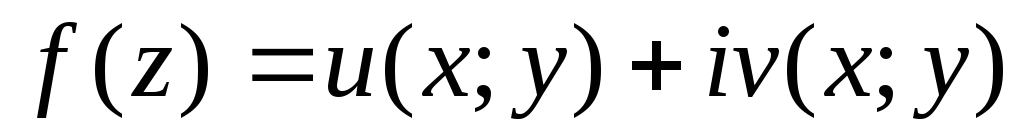.(выделение действительной и мнимой части функции.

Задача 8. Выделить действительную и мнимую части функций:

; ; ; .

5. Проверка функций на аналитичность. Условия Коши – Римана.

Задача 9. Выделив действительную и мнимую части функции выяснить, аналитична ли она в заданной точке.