9. Вычислим средний за период поток энергии через поперечное сечение волновода.

Для этого проинтегрируем выражения для плотности активного потока энергии по площади поперечного сечения волновода. Чтобы перейти к декартовым координатам, необходимо умножить среднее значение вектора Пойнтинга на единичную орту , так как перпендикуляр к сечению направле поz. Взяв двойной интеграл с пределами по размерам стенок волновода, получим:

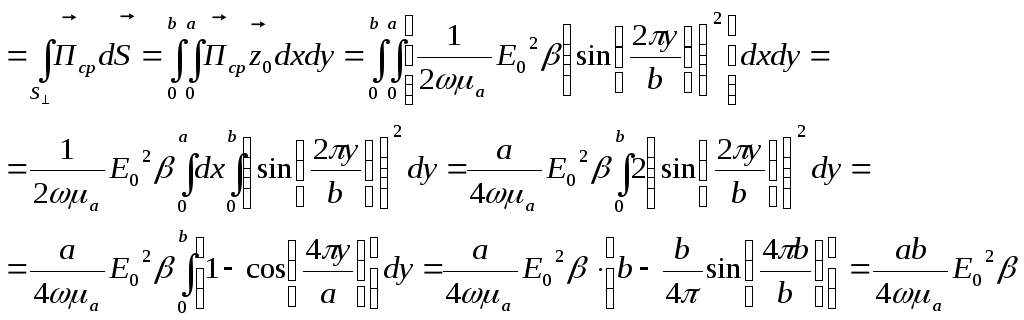(16)

Подставив в полученное выражение все необходимые значения констант и параметров для , найдём численное значение среднего за период потока энергии, проходящей через поперечное сечение трубы. Получим:

Вт

10. Фазовая скорость и скорость распространения энергии.

Фазовую скорость вычисляем по формуле:

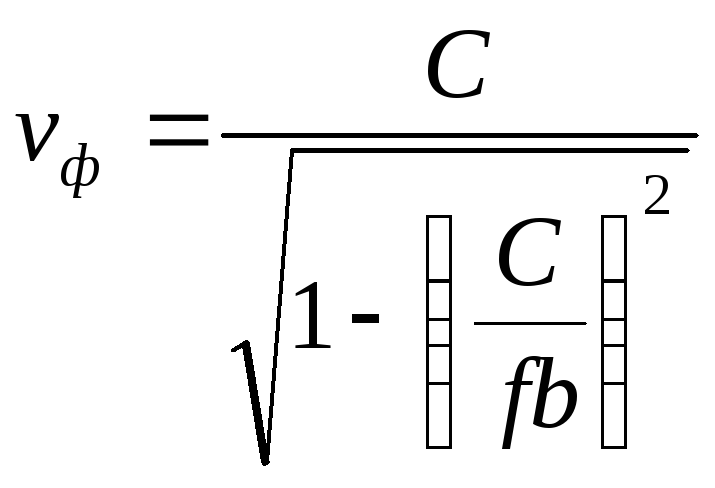
Подставив в формулу значения констант, получим:

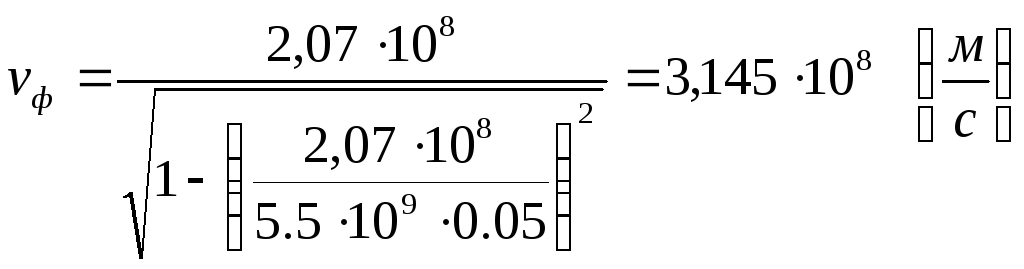
Фазовая скорость и скорость распространения энергии связаны следующим соотношением:

[источник 1, стр.262]

Отсюда скорость распространения энергии равна:

Подставив в написанную выше формулу значения констант, получим:

Графики зависимостей V_фи V_эот частоты, запрограммированные в пакетеMathCad14, приведены на рис.14.

Из графика видно, что при критической частоте фазовая скорость стремится к бесконечности, а скорость распространения энергии равна нулю. Если частоты выше критической, то фазовая скорость уменьшается, а скорость распространения энергии увеличивается. При этом обе скорости стремятся к скорости света в данной среде.

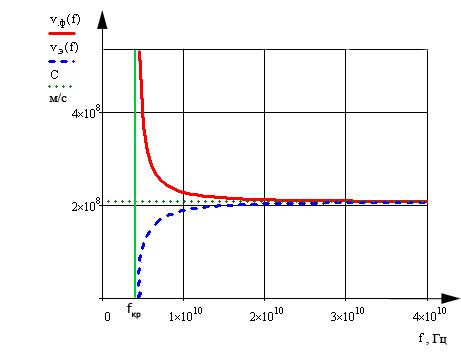
рис. 14

11. Определим коэффициента затухания волны.

Учтём, что стенки волновода выполнены из реального металла, проводимость которого равна

_{Закон изменения энергии вдоль оси z выглядит следующим образом:}

Рассмотрим прохождение энергии через элементарный объём, ограниченный стенками волновода и двумя плоскостями, перпендикулярными оси z. Плоскости расположим в крайних сечения (положения 0 и 1 м). Тогда:

(17)

Разложим в ряд Тейлора:

Учитывая только два первых члена, подставим ряд в формулу (17) и выразим коэффициент затухания:

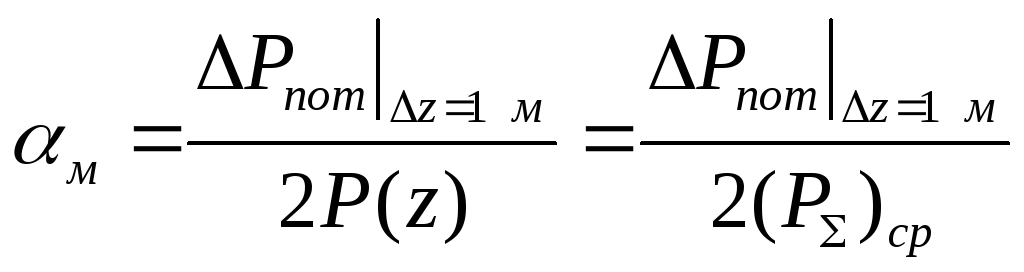
Для определения мощности потерь в стенках воспользуемся формулой:

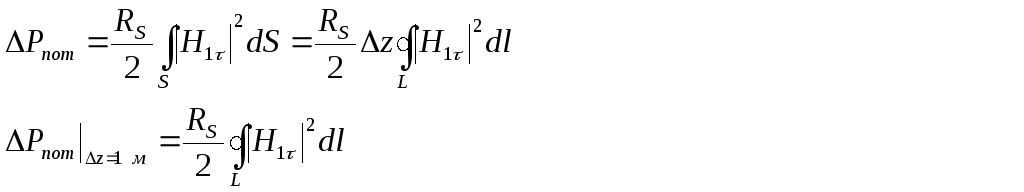
Таким образом, формула для коэффициента затухания волны будет иметь вид:

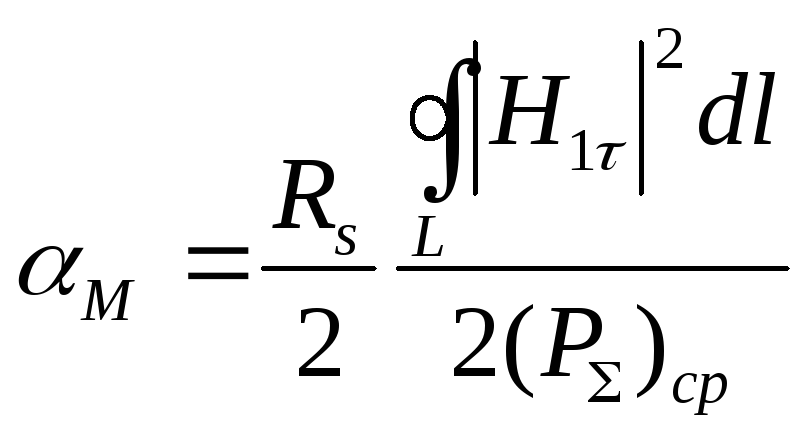, где

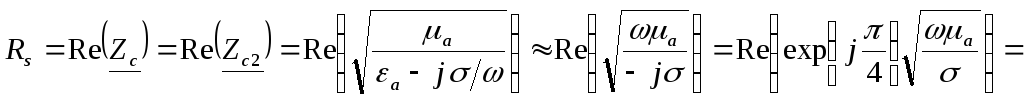
[источник 1, стр.213]

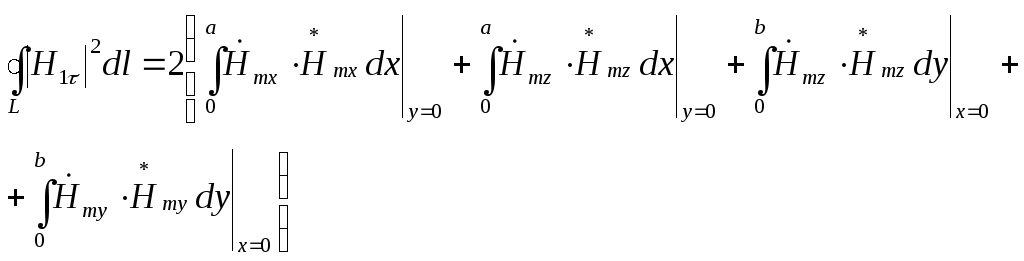
Вычислим отдельно произведения, используя выражения (9) и (15), (10) и (16):

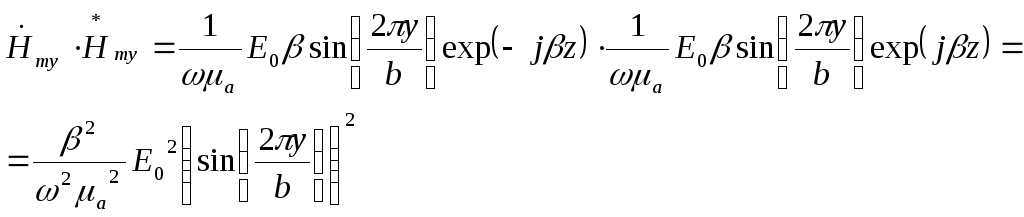
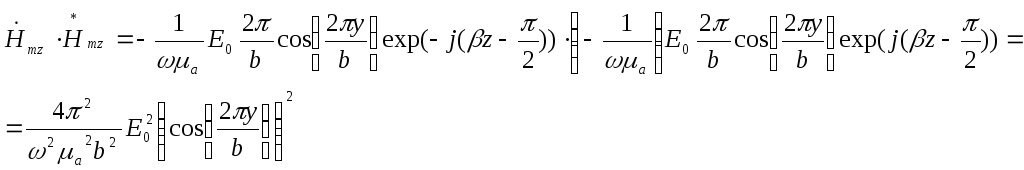
Вычислим интегралы, пользуясь подобным решением, осуществлённым в пункте 9:

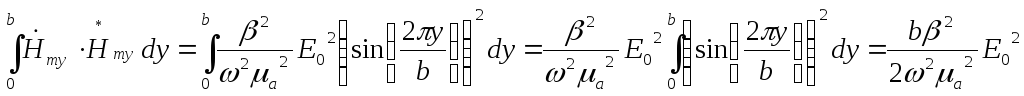
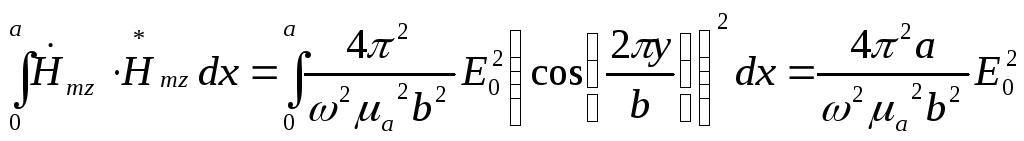
(при условии, что y=0 иcos(0)=1)

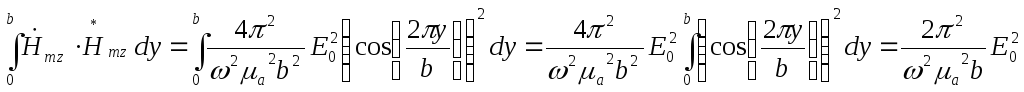
Подставим взятые интегралы в формулу:

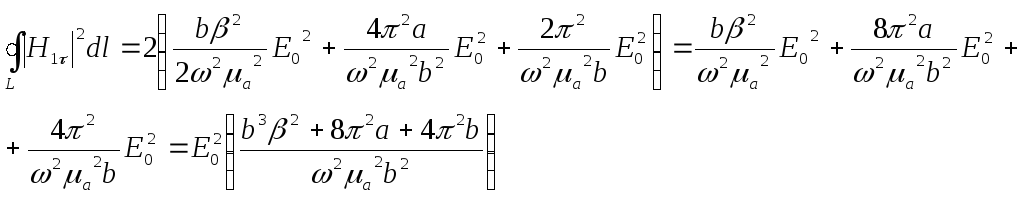
После упрощений выражение для коэффициента затухания примет вид:

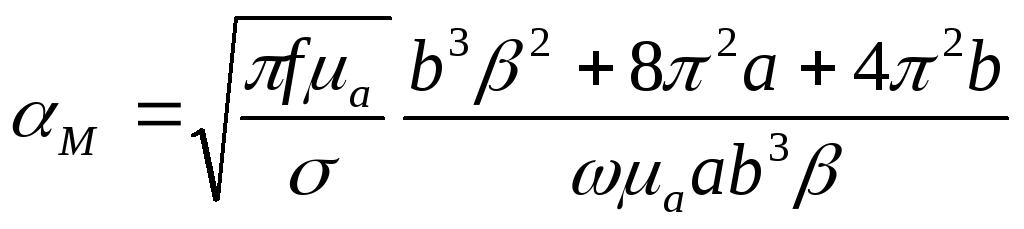
Выражение для Р_срподставлено из (16).

Подставив в полученное выражение для коэффициента затухания, получим:

, Нп/м

13. Рассчитаем и построим график зависимости коэффициента затухания волны в волноводе от частоты.

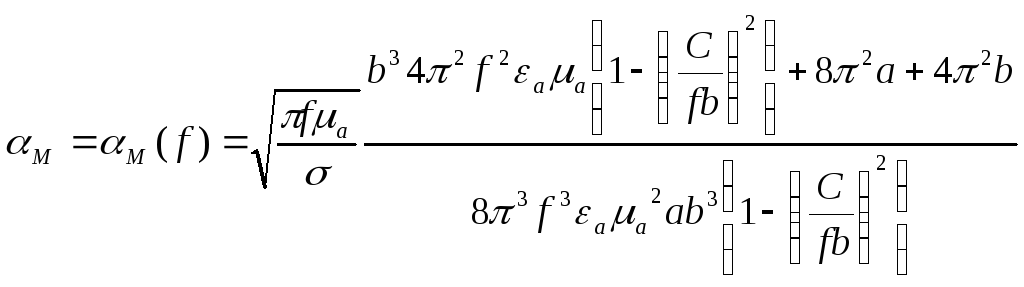
График этой зависимости, запрограммированной в пакете MathCad14, представлен на рис. 15.

Из графика видно, что процесс действительно затухающий (с ростом частоты уменьшается коэффициент затухания). При приближении к критической частоте наблюдаются большие потери энергии, а при удалении от критической частоты мы видим резкое падение затухания.

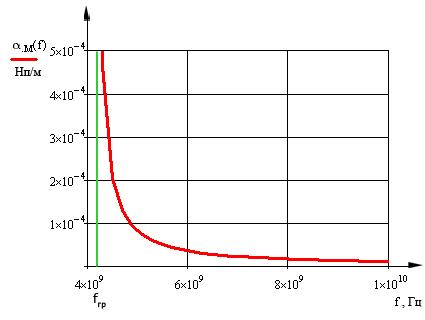
рис. 15

14. Определим тип волны, распространяющейся в волноводе. Изобразим структуру силовых линий электрического и магнитного полей этой волны и плотности поверхностного тока проводимости, протекающего по стенкам волновода.

Данная волна является волной типа . Такой вывод можно сделать, исходя из того, что имеетсясоставляющая, но нет составляющей, а также из рисунков 2 и 5, отражающих зависимостьz-составляющей вектора напряжённости магнитного поля от координатxиy. Вдоль х поле распределено равномерно, а вдольyукладывается одна полуволна. Структуры полей волны и поверхностных токов представлены на рисунках 16 и 17.