
- •«Анализ электромагнитного поля в прямоугольном волноводе»
- •Содержание
- •1. Техническое задание.
- •2. Пользуясь уравнениями Максвелла, определим комплексные амплитуды составляющих вектора .
- •3. Определим диапазон частот, в котором – действительное число, т.Е. Рассматриваемое поле – бегущая волна.
- •4. Запишем выражения для мгновенных значений составляющих векторов поля и для двух случаев:
- •5. Построим графики амплитуд составляющих векторов поля.
- •6. Проверка выполнения граничных условий.
- •7. Комплексные амплитуды плотностей поверхностных токов и зарядов.
- •8. Определим выражения для комплексного вектора Пойнтинга, среднее за период значение плотности потока энергии, амплитуду плотности реактивного потока энергии.
- •9. Вычислим средний за период поток энергии через поперечное сечение волновода.
- •10. Фазовая скорость и скорость распространения энергии.
- •11. Определим коэффициента затухания волны.
- •13. Рассчитаем и построим график зависимости коэффициента затухания волны в волноводе от частоты.
- •15. Вывод.
- •16. Список использованной литературы.
6. Проверка выполнения граничных условий.
В этом пункте мы должны проверить
выполнение граничных условий для
касательных составляющих вектора ![]() и нормальной составляющей вектора
и нормальной составляющей вектора![]() на верхней стенке трубы
на верхней стенке трубы![]() .
.
Для верхней стенки трубы
![]() (рис.12) касательными составляющими
вектора электрического поля являются
составляющие
(рис.12) касательными составляющими
вектора электрического поля являются
составляющие![]() и
и![]() ,
а нормальной составляющей вектора
магнитного поля является составляющая
,
а нормальной составляющей вектора
магнитного поля является составляющая![]() .
Данные выражения ранее были получены
нами (11).
.
Данные выражения ранее были получены
нами (11).
Проверка граничных условий на границе
раздела сред диэлектрик – идеальный
металл заключается в проверке истинности
утверждений
![]() и
и![]() ,
т.е. равенства нулю касательной вектора
,
т.е. равенства нулю касательной вектора![]() и нормальной вектора
и нормальной вектора![]() проекций (составляющих).
проекций (составляющих).
Подставим в рассматриваемые выражения (11) y=b, получим:
![]()
при этом другие множители от координаты yне зависят.
Следовательно, оба выражения обращаются в ноль и граничные условия на границе раздела сред диэлектрик – идеальный металл выполняются.
7. Комплексные амплитуды плотностей поверхностных токов и зарядов.
Комплексные амплитуды плотностей поверхностных токов определяются следующими соотношениями:
![]() [источник 1, стр.279]
[источник 1, стр.279]
Комплексные амплитуды плотностей поверхностных зарядов определяются следующими соотношениями:
![]()
Вышеизложенные соотношения справедливы на границе раздела сред диэлектрик – идеальный металл.
Для боковой стенки трубы
![]() (рис.13) нормаль противоположна вектору
(рис.13) нормаль противоположна вектору![]() :
:![]() .
.
Касательными к этой стенке составляющими
вектора
![]() являются составляющие вдоль осейyиz, то есть:
являются составляющие вдоль осейyиz, то есть:
![]()
Подставим это выражение в формулу плотности токов. Тогда комплексная амплитуда плотности поверхностных токов будет равна:
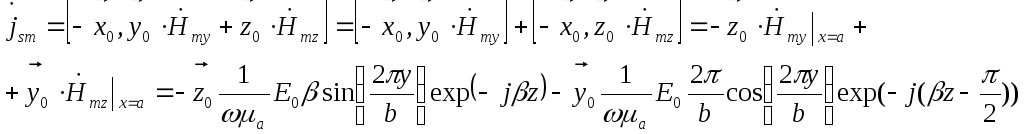
Подставив константы, рассчитанные в п.5, получим:
![]()
Нормальной к этой стенке составляющей
вектора
![]() будет
составляющая
будет
составляющая![]() .
.
![]()
Подставив константы, рассчитанные в п.5, получим:
![]()
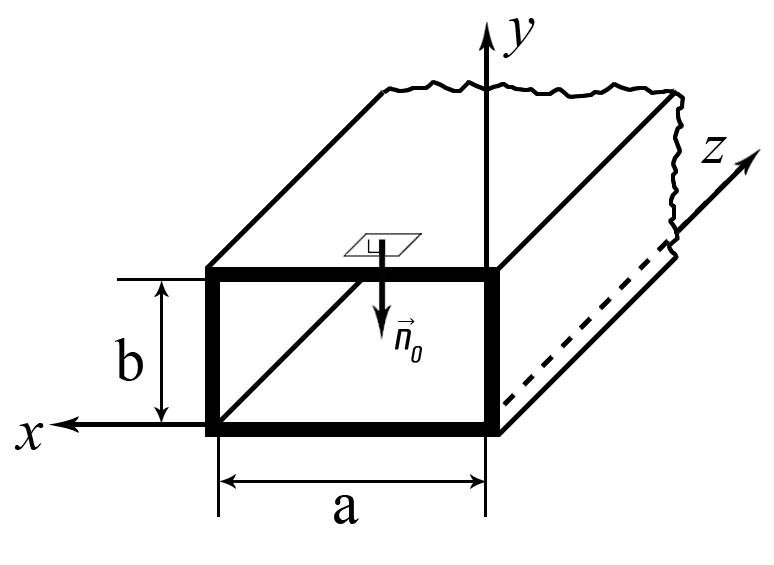
рис.12
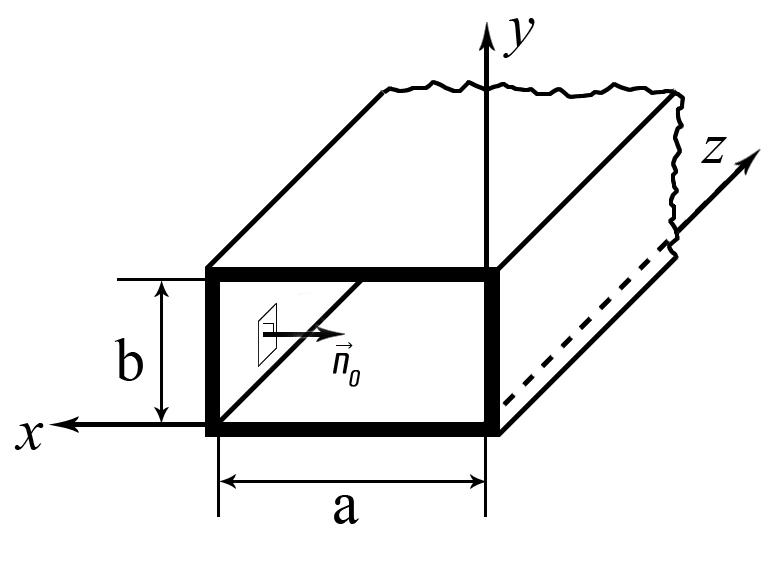
рис.13
8. Определим выражения для комплексного вектора Пойнтинга, среднее за период значение плотности потока энергии, амплитуду плотности реактивного потока энергии.
Комплексный вектор Пойнтинга определяется как половина векторного произведения комплексной амплитуды вектора напряжённости электрического поля на комплексно сопряжённое комплексной амплитуды вектора напряжённости магнитного поля. Составляющие полей нам известны, подставляем их в формулу [источник 1, стр.57], упрощаем выражение.
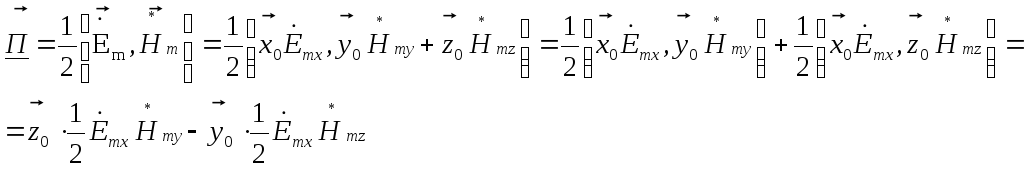
1)
![]()
Рассмотрим сначала режим бегущей волны.
Запишем выражения для комплексно
сопряжённых составляющих вектора
![]() .
Для этого поменяем знак в выражениях
(9) и (10) перед мнимой единицей:
.
Для этого поменяем знак в выражениях
(9) и (10) перед мнимой единицей:
![]() (15)
(15)
![]() (16)
(16)
С учётом этих равенств и выражения (1), вектор Пойнтинга примет вид:
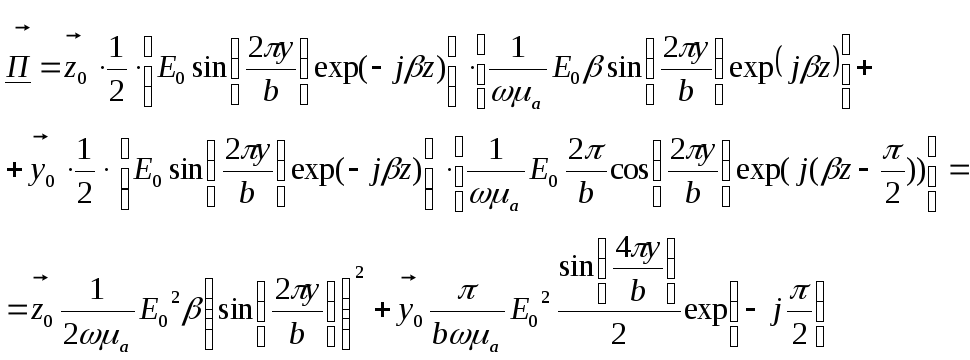
Подставив константы, рассчитанные в п.5, получим:
![]()
Заметим, что составляющая по оси у чисто мнимая, а составляющая по оси z – действительная, значит вдоль z и происходит перенос энергии. Среднее за период значение плотности потока энергии тогда:
![]()
![]()
А амплитуда плотности реактивного потока энергии будет равна:
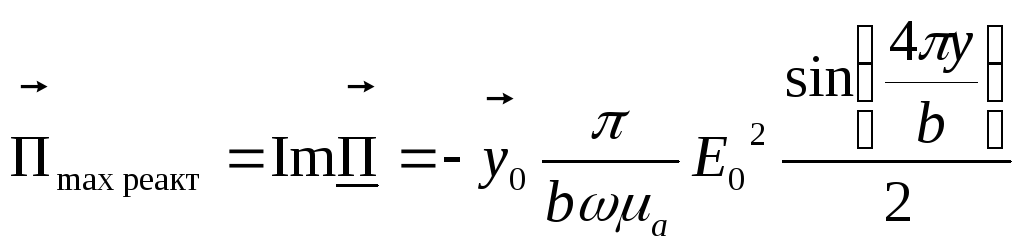
Подставив константы, рассчитанные в п.5, получим:
![]()
![]()
![]()
2)
![]()
Для второго случая комплексно сопряжённые
составляющие вектора
![]() примут вид (делаем в выражениях (9) и (10)
замену
примут вид (делаем в выражениях (9) и (10)
замену![]() и меняем знак перед мнимой единицей):
и меняем знак перед мнимой единицей):
![]()
![]()
С учётом этих равенств и применив вышеуказанную замену к выражению (1), вектор Пойнтинга примет вид:
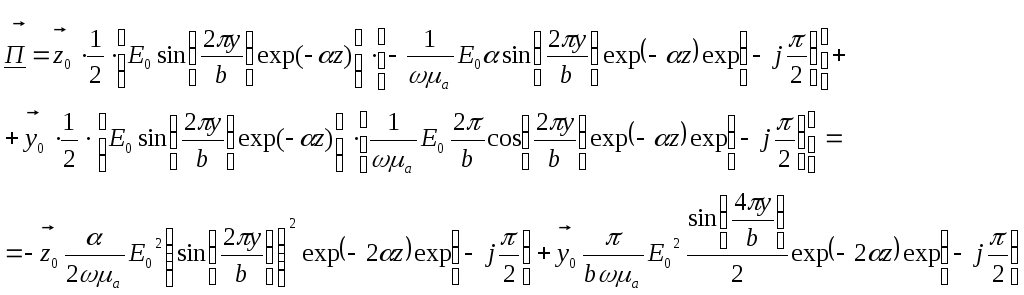 Подставив константы, рассчитанные в
п.5, получим:
Подставив константы, рассчитанные в
п.5, получим:
![]()
В этом случае вектор Пойнтинга чисто мнимый и переноса энергии не происходит.
![]() 0
0
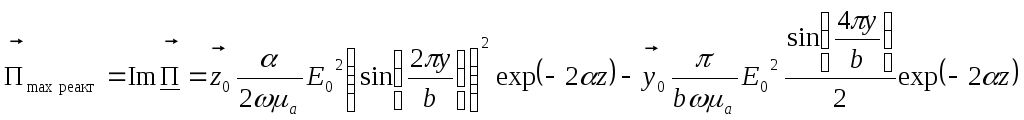
П![]() одставив
константы, рассчитанные в п.5, получим:
одставив
константы, рассчитанные в п.5, получим:
