МТУСИ

Кафедра математического анализа

2012/2013 уч.г.

Индивидуальное задание по алгебре и геометрии (для студентов группы бфи 1201, второй семестр)

Задача 1. Образует ли данное множество функций на отрезке линейное пространство относительно обычных операций сложения и умножения на число:

1. Множество функций, непрерывных на отрезке.

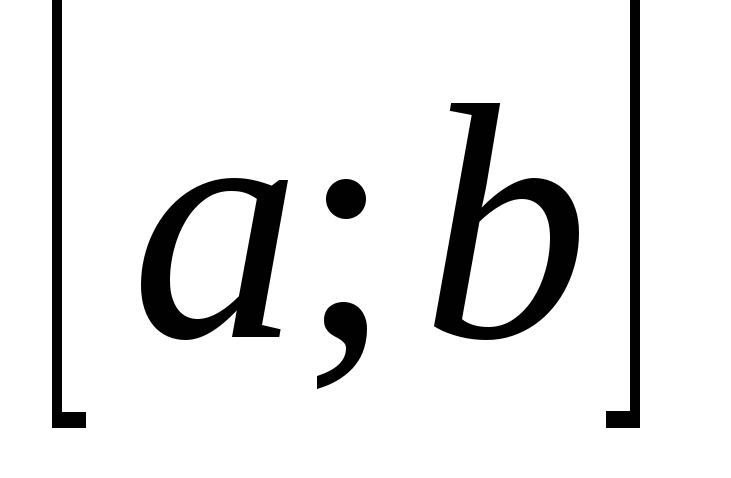2. Множество функций, дифференцируемых на отрезке.

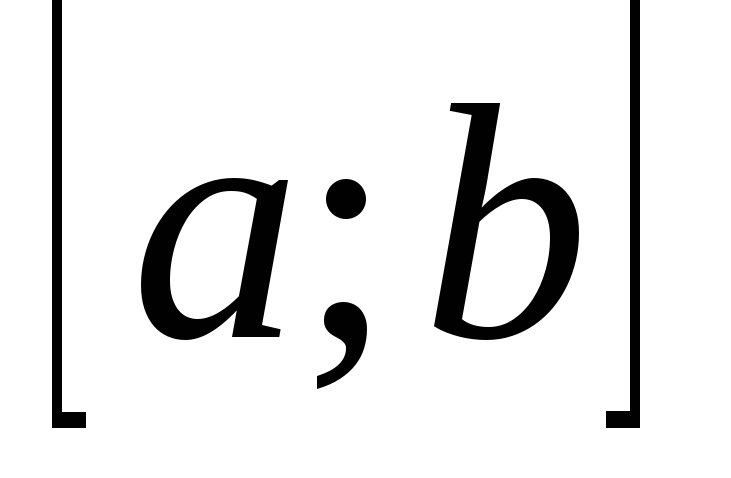3. Множество функций, интегрируемых на отрезке.

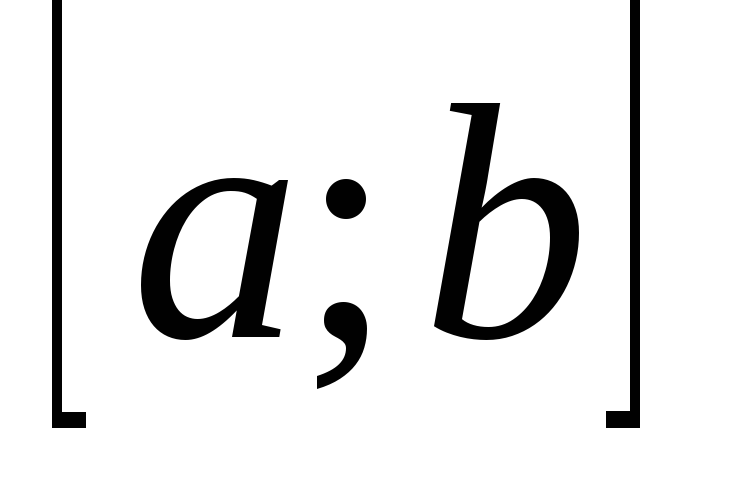4. Множество функций, ограниченных на отрезке.

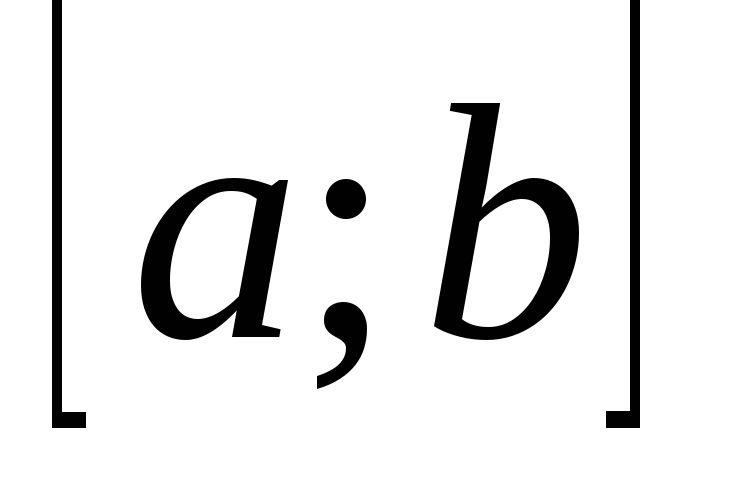5. Множество функций таких, что

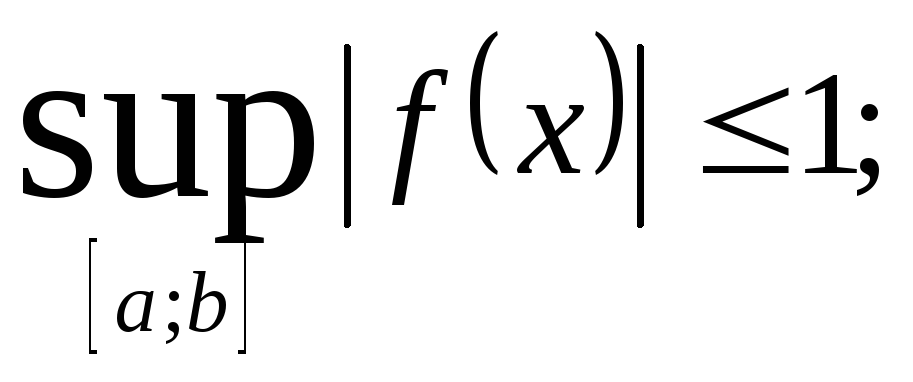
6. Множество функций, неотрицательных на отрезке.

7. Множество функций таких, что

8. Множество функций таких, что

9. Множество функций таких, что

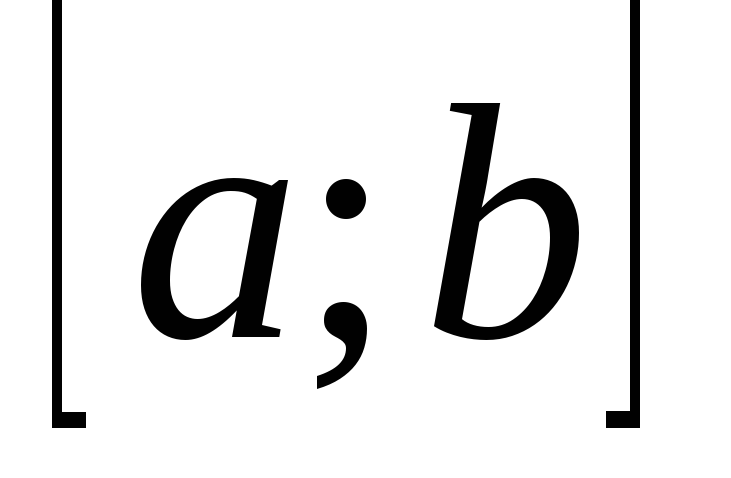10. Множество функций, монотонно возрастающих на отрезке.

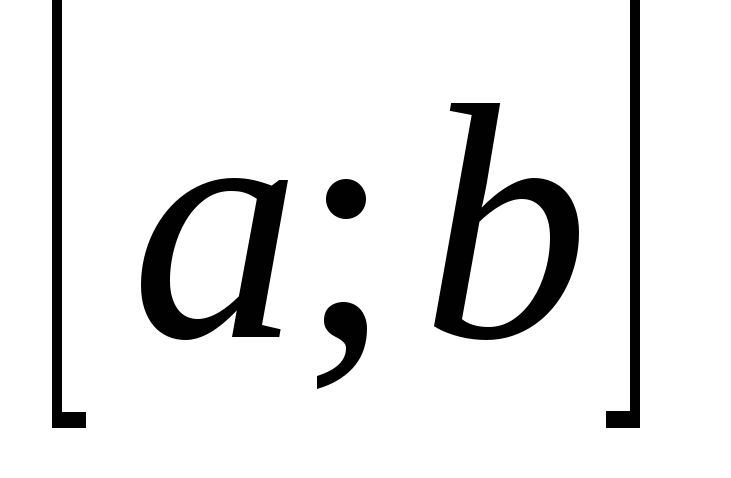11. Множество функций, монотонно убывающих на отрезке.

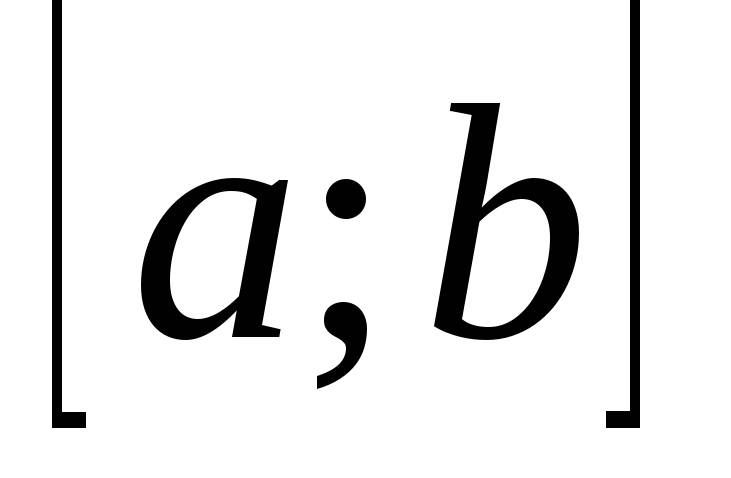12. Множество функций, монотонных на отрезке.

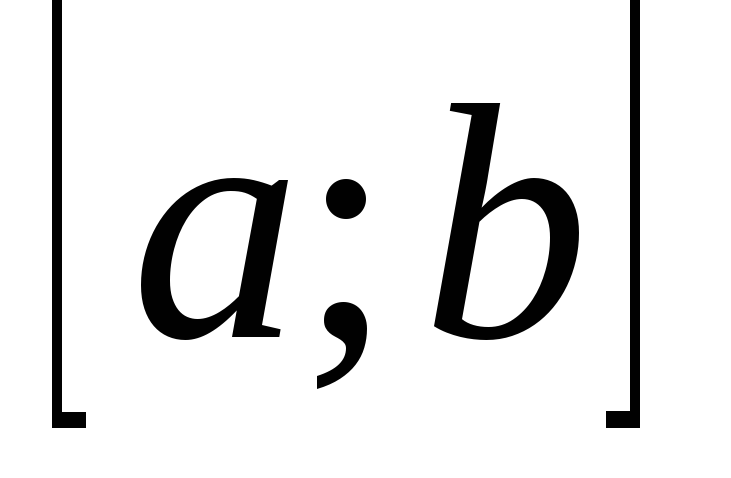Задача 2. Является ли данная система векторов линейно независимой:

1.

2.

3.

4.

5.

6.

7.

8.

9.

10.

11.

12.

Задача 3. Образуют ли матрицы 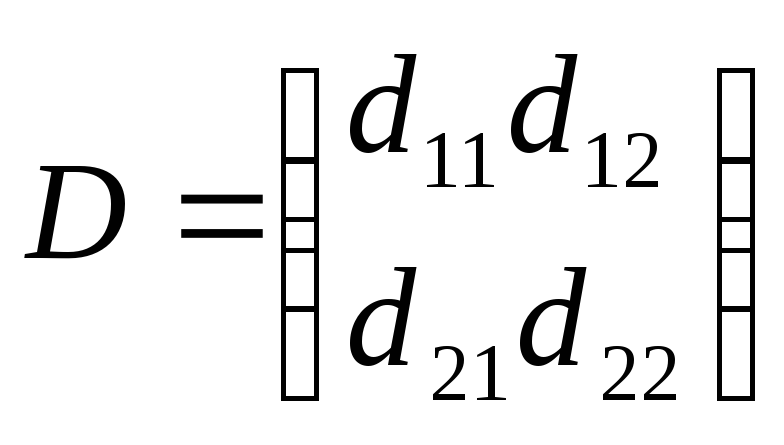базис пространства матриц размерности 2X2? Если да, то разложить матрицу по этому базису.

1 2 3 4 5 6 7 8 9 10 11 12	1 0 -1 3 2 -4 2 0 5 -4 2 1	4 3 -3 -2 -1 2 1 3 1 2 5 3	-2 -3 0 1 0 -3 1 0 -2 -1 3 -3	1 2 -4 1 2 -1 5 -3 -2 0 -4 0	3 2 4 5 4 2 1 0 9 0 0 1	-1 -6 -3 -3 -3 -2 -4 -3 4 2 1 2	3 5 6 -5 -3 0 0 1 0 -2 3 3	3 2 -1 -2 -6 0 -3 -1 2 3 4 2	2 -1 0 0 6 4 3 2 1 -2 -3 -1	2 1 5 0 0 0 3 5 1 -1 -3 -4	0 0 -6 -7 5 4 5 6 3 2 1 1	0 3 -2 -2 -5 -5 0 0 0 0 0 2

1 2 3 4 5 6 7 8 9 10 11 12	3 0 0 2 2 1 1 4 5 0 0 0	3 -2 -1 -6 4 -4 3 -2 -2 -5 -2 -3	0 3 2 1 4 -3 -2 4 -1 2 2 3	3 -3 -3 -2 -1 1 1 2 3 3 3 4	3 2 -4 -3 -2 -1 3 2 5 4 -2 -1	2 3 -2 -4 -6 -5 6 4 5 3 2 -1	3 2 -2 -2 1 4 2 1 -2 2 1 0	0 2 6 -5 -3 3 2 -1 2 3 1 1

Задача 4. Пусть и координаты векторов и соответственно в некотором базисе двумерного вещественного линейного пространства. Определить, может ли заданная функция служит скалярным произведением, а в случае, если не может – указать, какие из свойств скалярного произведения не выполняются:

1. .

2. .

3. .

4. .

5. .

6. .

7. ..

8. .

9. .

10. .

11. .

12.

Задача 5. Найти площадь и внутренние углы треугольника :

Задача 6. Образуют ли данная система векторов базис трехмерного евклидова пространства? Если да, то применяя процесс ортогонализации и нормирования, получить ортонормированный базис пространства со стандартным скалярным произведением:

1.

2.

3.

4.

5.

6.

7.

8.

9.

10.

11.

12.

Задача 7. Даны два линейных преобразования

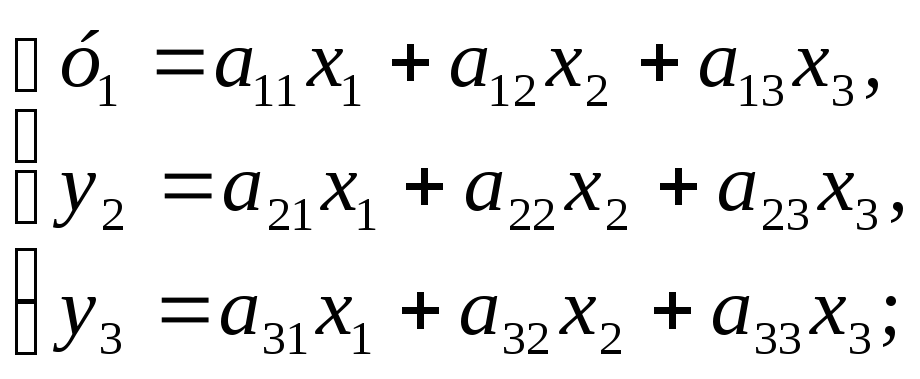
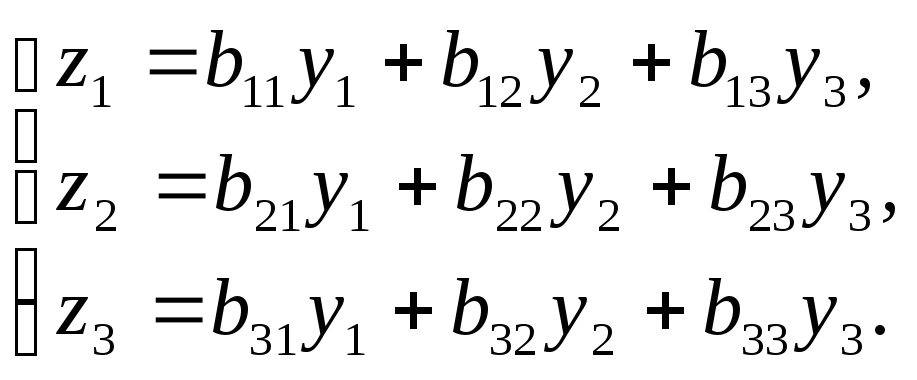
Средствами матричного исчисления найти преобразование, выражающее через.

1 2 3 4 5 6 7 8 9 10 11 12	1 2 -3 4 2 -2 4 3 1 4 6 3	-3 -2 -1 2 5 6 4 3 2 -1 -3 -4	3 4 2 5 1 2 3 2 1 2 1 3	3 -4 -3 -6 -5 -3 -2 -1 5 4 3 2	-1 -2 -4 -7 -6 -5 -8 -4 -3 8 6 7	2 4 3 5 6 7 5 3 2 1 3 4	-3 -3 -4 -7 -6 8 4 6 -3 -2 -1 -4	1 3 2 4 5 3 7 8 3 2 1 5	2 -5 -7 -6 5 4 6 3 2 8 6 7	2 3 4 5 2 3 4 1 2 3 3 3	-2 -3 -4 -5 -3 4 5 8 2 -1 -3 -2	3 9 7 3 2 1 2 5 4 6 7 8	4 -3 -9 -3 -7 -5 -3 -3 2 4 3 1	8 4 3 1 6 7 9 4 3 1 2 5	4 3 -3 -4 -2 -1 -3 -4 5 -5 -4 -6	5 6 4 7 8 4 3 2 1 1 3 4	7 6 5 4 -4 -4 -3 -6 -2 -4 -4 5	6 5 6 4 3 4 2 2 2 1 2 3

Задача 8. Дана матрица линейного преобразования в базисе. Найти матрицу этого линейного преобразования в базисе.

Задача 9. Квадратичная форма задана матрицей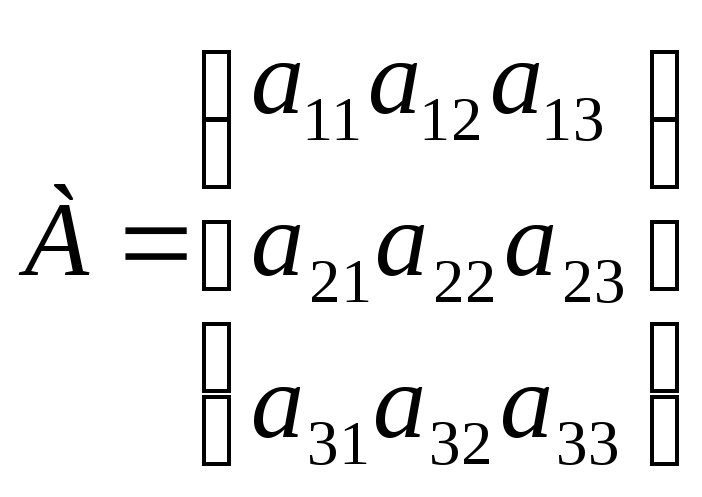 в стандартном базисе.

1. С помощью критерия Сильвестра определить, является ли эта квадратичная форма знакоопределенной;

2. Привести квадратичную форму, заданную матрицей, методом Лагранжа к нормальному виду. Записать соответствующие формулы замены координат.

1 2 3 4 5 6 7 8 9 10 11 12	1 2 1 9 7 1 2 2 2 5 1 5	1 -1 1 -6 -2 2 1 2 -1 -2 2 2	3 0 2 -3 0 -4 0 1 -2 -1 -5 3	1 -1 1 -6 -2 2 1 2 -1 -2 2 2	5 1 1 4 6 -2 2 2 5 2 -2 -1	1 1 2 2 -2 -2 0 1 1 -2 2 0	3 0 2 -3 0 -4 0 1 -2 -1 -5 3	1 1 2 2 -2 -2 0 1 1 -2 2 0	1 2 4 1 5 1 -5 3 2 5 1 1

Задача 10. Привести к каноническому виду уравнение линии второго порядка и построить ее.

Задача 11. Решить задачу линейного программирования графическим методом.

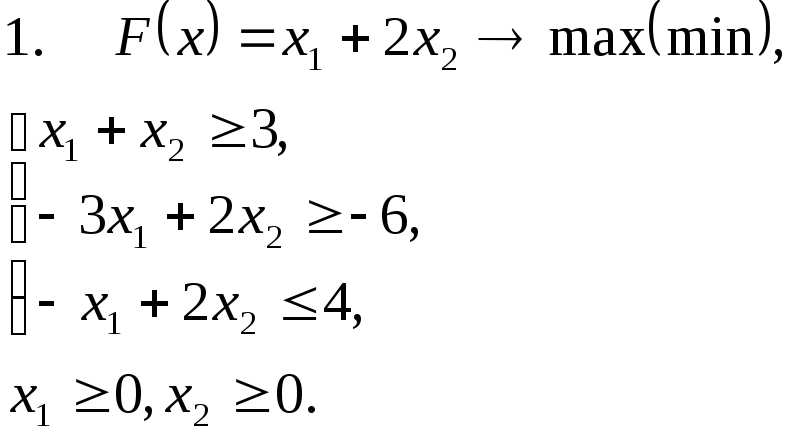
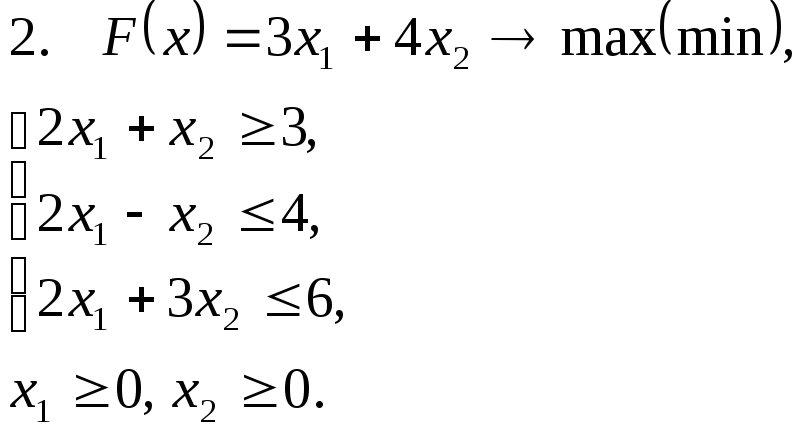
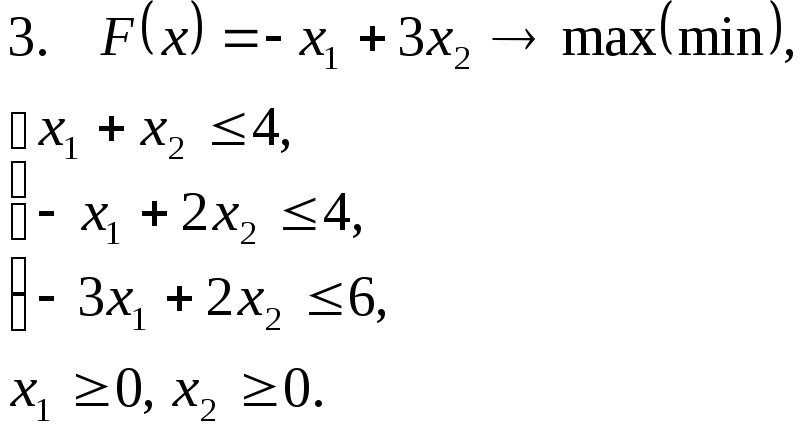
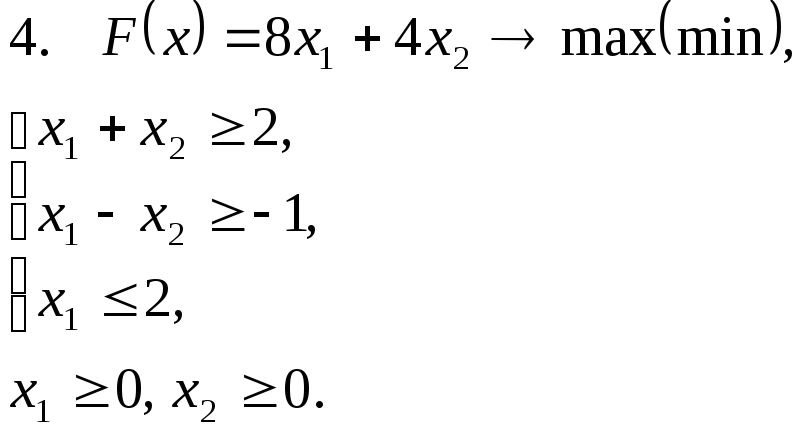
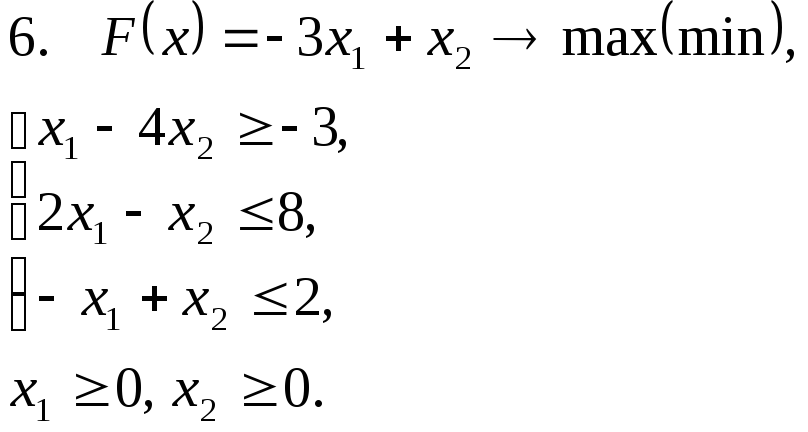
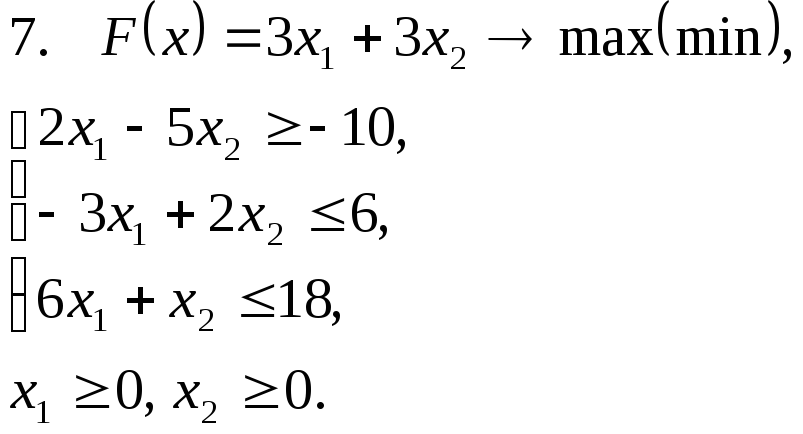
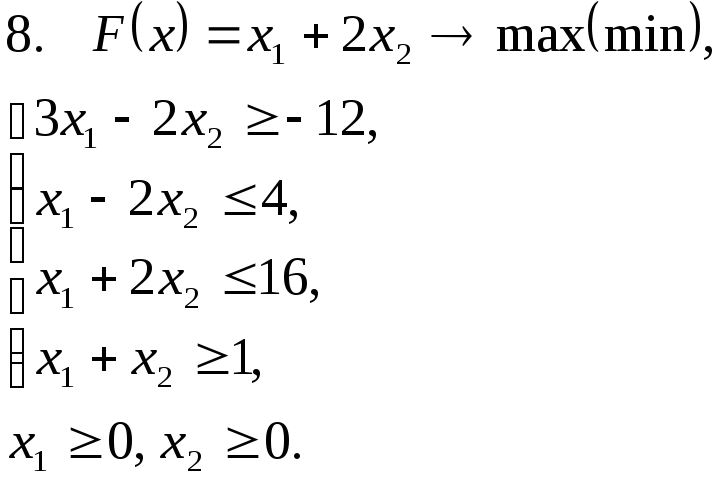
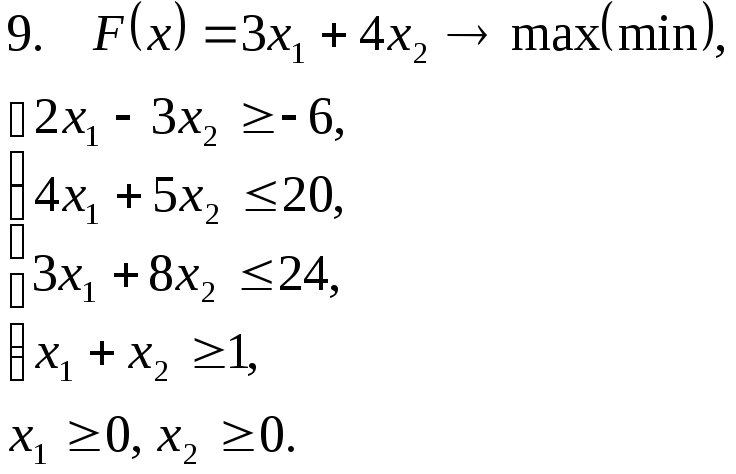
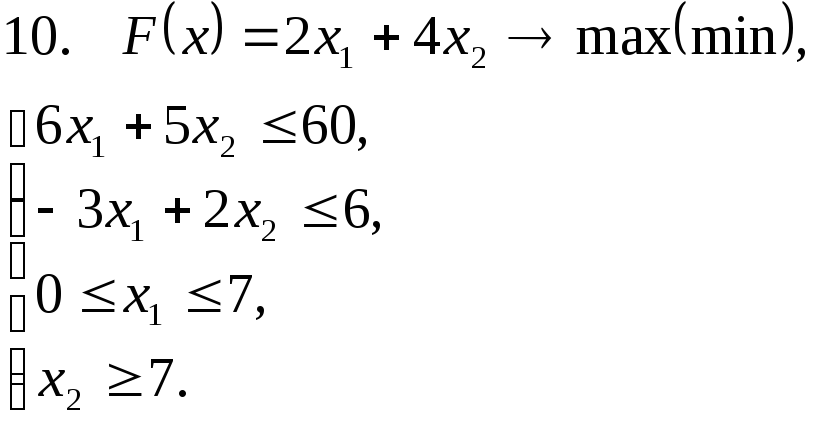
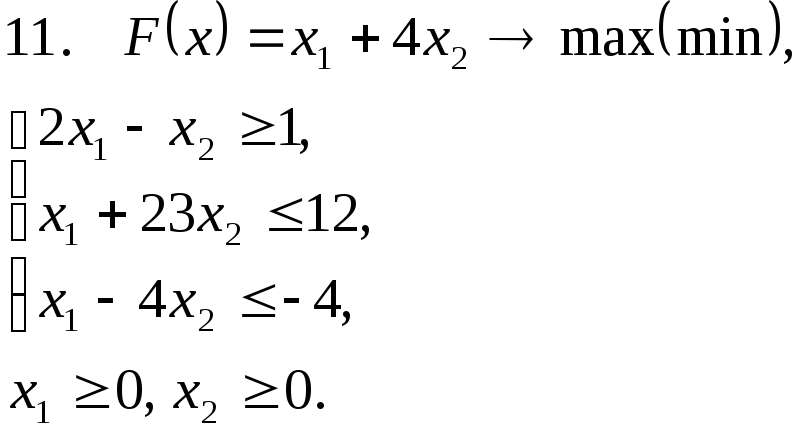
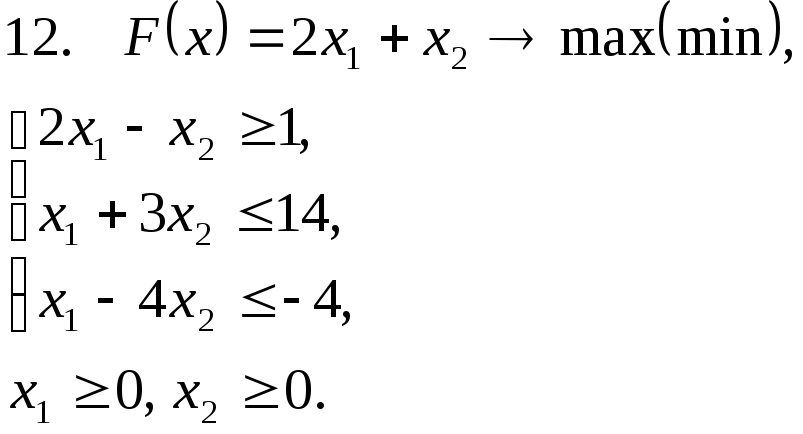
Задача 12. Для заданной задачи составить двойственную и найти решение обеих задач симплекс-методом.

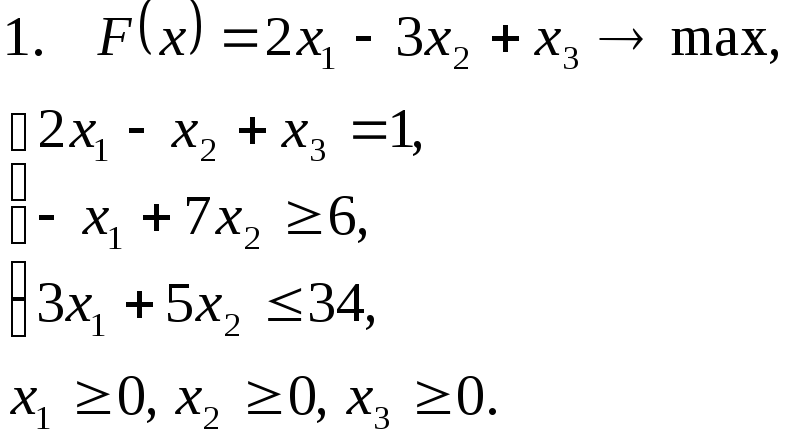
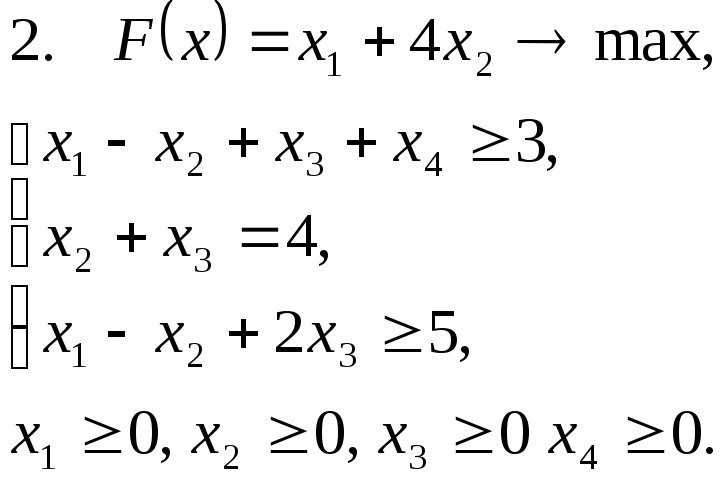
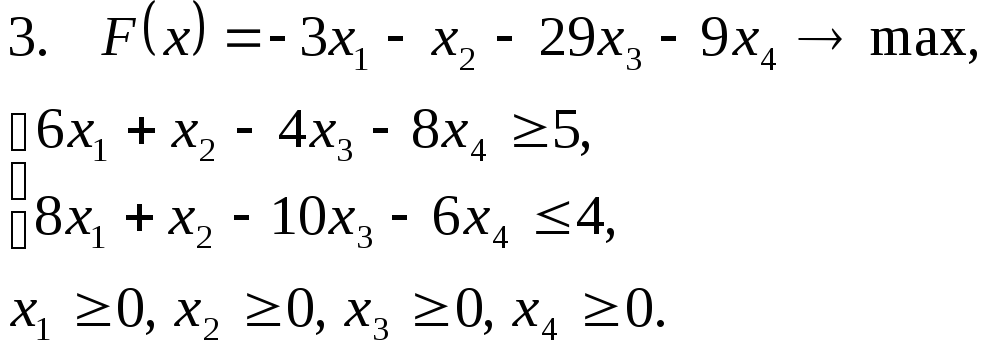
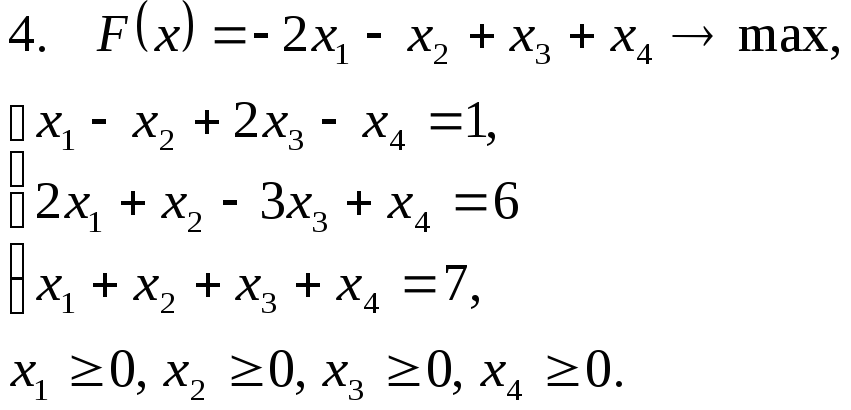
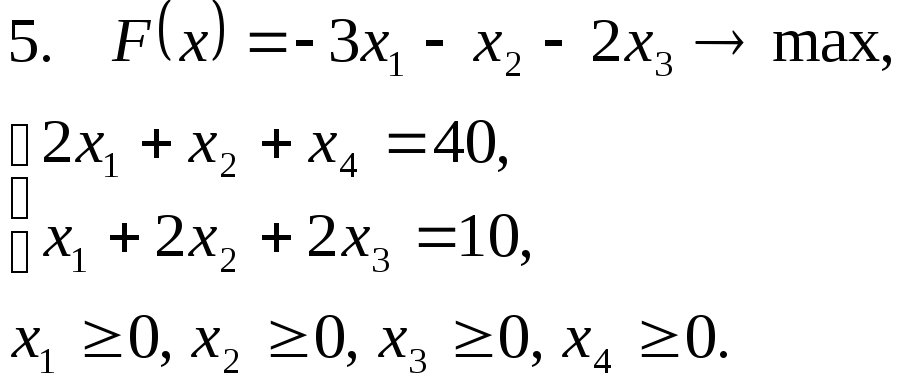
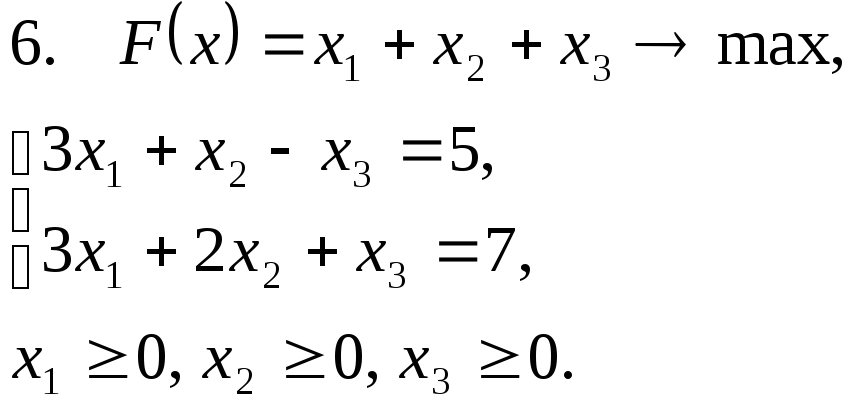
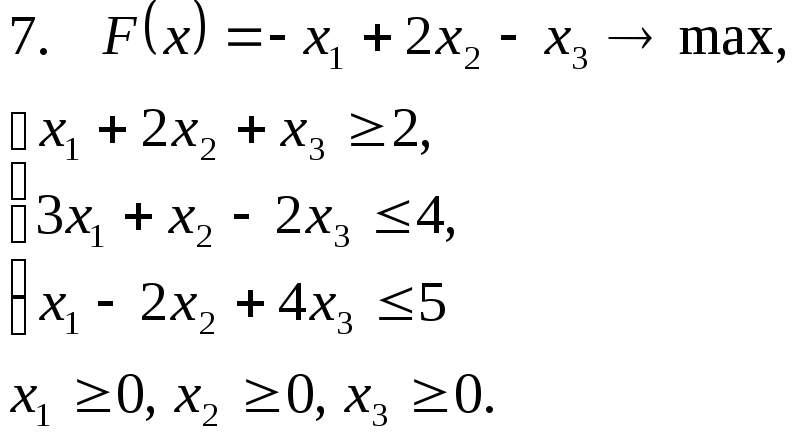
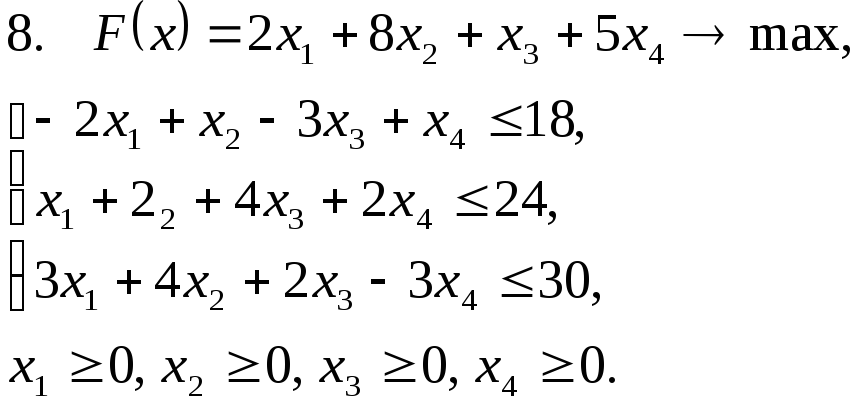
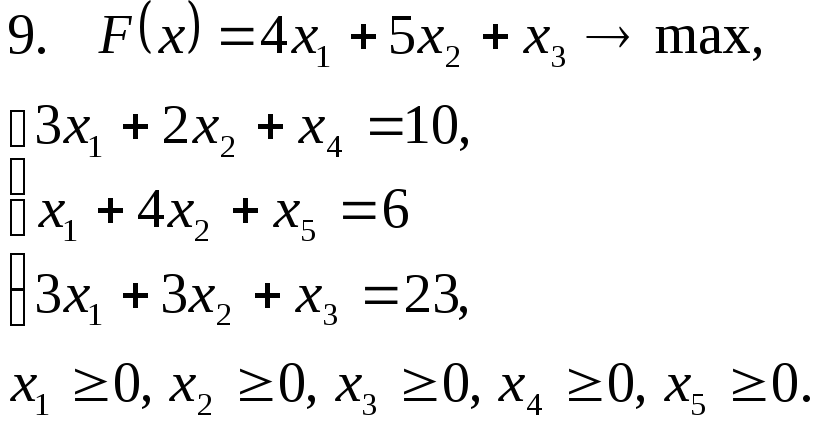
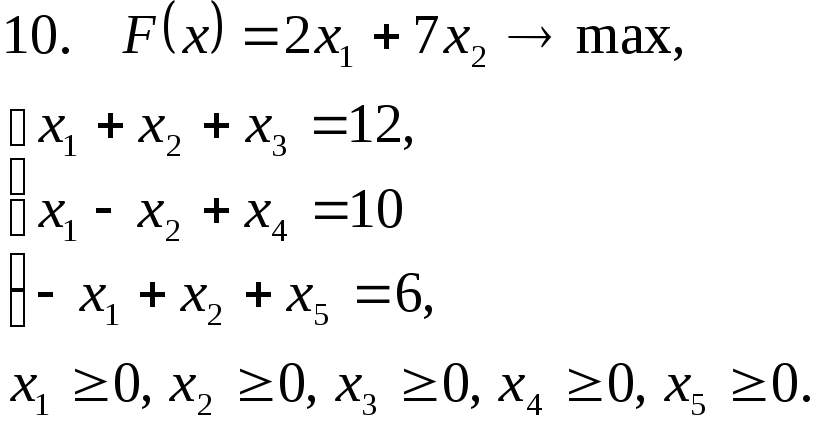
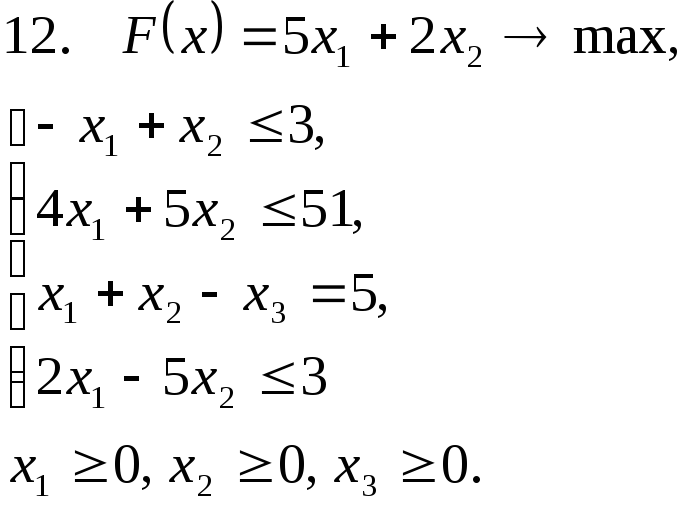
Задача 13. Решить транспортную задачу.

	5	4	3	2	120
5		2	1	4	70
7	4			3	80
	30	40	100	10

1. 1)90, 2, 3, 1, 5;

2) 70, 4, 1, 5, 7.

2. 1)90, 5, 1, 4, 6;

2) 105, 4, 4, 5, 1.

3. 1)90, 4, 3, 2, 8;

2) 80, 3, 1, 4, 5.

4. 1)90, 2, 7, 6, 1;

2) 95, 9, 1, 7, 2.

5. 1)90, 3, 4, 5, 3;

2) 75, 5, 8, 5, 2.

6. 1)90, 5, 2, 4, 1;

2) 100 4, 3, 5, 9.

7. 1)90, 4, 6, 1, 8;

2) 60, 6, 10, 6, 2.

8. 1)90, 2, 9, 4, 2;

2) 95, 5, 1, 2, 11.

9. 1)90, 12, 3, 1, 7;

2) 110, 4, 4, 15, 2.

10. 1)90, 5, 1, 4, 6;

2) 65, 4, 4, 5, 1.

11. 1)90, 5, 3, 8, 1;

2) 80, 7, 1, 8, 2.

12. 1)90, 5, 6, 2, 1;

2) 125, 4, 11, 7, 12.